Estudio completo de funciones trigonométricas
Estudia y representa las siguientes funciones trigonométricas:
1) y = sen (5x)
2) y = 2 cos(x)
3) y = cotg(2x)
4) y = tg(x/4)
5) y = 3 + 2cos(x/2)
6) y = 3 sec(x)
7) y = - 3 + arc cos(x)
8) y = sen2(x)
Funciones trigonométricas: periodo, amplitud, asíntotas verticales, dominio e imagen.
| Periodo | Amplitud | Asintotas verticales |
Dominio | Imagen | |
|---|---|---|---|---|---|
| y = sen x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = cos x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = tg x | π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | R | |
| y = cotg x | π | k·π , k∈Z | { x∈R | x ≠k·π } | R | |
| y = sec x | 2π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | { y∈R | y ≤ -1 ó y ≥ 1 } | |
| y = cosec x | 2π | k π , k∈Z | { x∈R | x ≠k·π } | { y∈R | y ≤ -1 ó y ≥ 1 } |
| y = sen x | y = cos x | |
|---|---|---|
| Periodo | 2π | 2π |
| Amplitud | 1 | 1 |
| Asintotas verticales | No tiene | No tiene |
| Dominio | R | R |
| Imagen | { y∈R | -1 ≤ y ≤ 1 } | { y∈R | -1 ≤ y ≤ 1 } |
| y = tg x | y = cotg x | |
|---|---|---|
| Periodo | π | π |
| Amplitud | ||
| Asintotas verticales | π/2 (2k + 1) , k∈Z | k·π , k∈Z |
| Dominio | { x∈R | x ≠ π/2 (2k + 1) } | { x∈R | x ≠k·π } |
| Imagen | R | R |
| y = sec x | y = cosec x |
|
|---|---|---|
| Periodo | 2π | 2π |
| Amplitud | ||
| Asintotas verticales | π/2 (2k + 1) , k∈Z | k π , k∈Z |
| Dominio | { x∈R | x ≠ π/2 (2k + 1) } | { x∈R | x ≠k·π } |
| Imagen | { y∈R | y ≤ -1 ó y ≥ 1 } | { y∈R | y ≤ -1 ó y ≥ 1 } |
Dada la siguiente función, estudia todas sus características. Representa su gráfica.
y = sen (5x)
1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = [-1 , 1]
3) Periodicidad:
Como la función seno es periódica de período 2π, la función f(x) = sen (5x) es periódica de período:
2π = 5x ⇔ x = 2π/5
Es periódica de período 2π/5 .
También podemos hallar el período de la función así:
f(x) = sen(5x) = sen(5x + 2π) = sen[ 5 (x + 2π/5) ] = f(x + 2π/5)
También podemos calcular el periodo de forma más fácil aplicando directamente la siguiente fórmula:
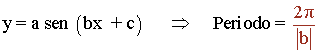
Periodo = 2π/5
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen 0 ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen (5x) ⇒ 5x = 0 ó 5x = π ⇒ x = 0 ó x = π/5 ⇒ (0 , 0) , (π/5 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
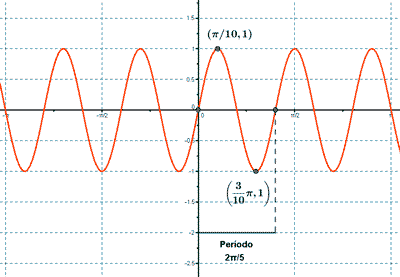
1 = sen (5x) ⇒ 5x = π/2 ⇒ x = π/10 ⇒ (π/10 , 1)
Los puntos mínimos de la función vendrán dados por la ecuación:
-1 = sen (5x) ⇒ 5x = 3π/2 ⇒ x = 3π/10 ⇒ (3π/10 , -1)
Dada la siguiente función, estudia todas sus características. Representa su gráfica.
y = 2 cos(x)
1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = [-2 , 2]
3) Periodicidad:
Como la función coseno es periódica de período 2π , la función f(x) = 2 cos(x) tiene el mismo período: 2π .
También podemos sacar el período de la función así:
f(x) = 2 cos(x) = 2 cos(x + 2π) = f(x + 2π)
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 ⇒ y = 2 ⇒ (0 , 2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos(x) ⇒ cos(x) = 0 ⇒ x = π/2 ó x = 3π/2
Luego los puntos de corte con el eje X son: (π/2 , 0) , (3π/2 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
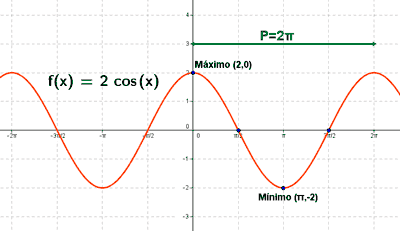
2 = 2 cos(x) ⇒ 1 = cos(x) ⇒ x = 0 ó x = 2π ⇒ (0 , 2) , (2π , 2)
Los puntos mínimos de la función vendrán dados por la ecuación:
-2 = 2 cos(x) ⇒ -1 = cos(x) ⇒ x = π ⇒ (π , -2)
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
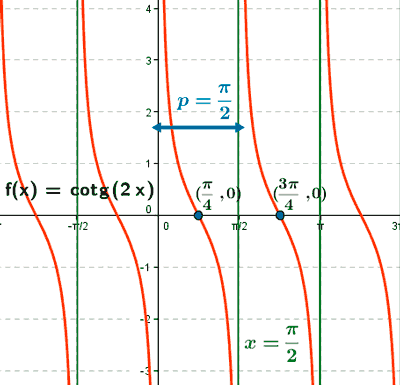
y = cotg(2x)
1) Dominio:
La función cotangente no está definida en: kπ , k ∈ Z
Por tanto, nuestra función tampoco estará definida en:
2x = kπ k ∈ Z ⇔ x = kπ/2 , k ∈ Z
Luego: Dom(f) = R - { kπ/2 | k ∈ Z }
2) Recorrido: Im(f) = R
3) Periodicidad:
Como la función cotangente es periódica de período π , la función f(x) = cotg (2x) es periódica de período:
2x = π ⇔ x = π/2
Es periódica de período π/2 .
También podemos sacar el período de la función así:
f(x) = cotg(2x) = cotg(2x + π) = cotg( 2(x + π/2) ) = f(x + π/2)
También podemos calcular el periodo de forma más fácil aplicando directamente la siguiente fórmula:
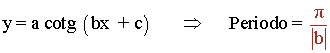
Periodo = π/2
4) Puntos de corte:
La función cotangente no corta al eje Y, por tanto, la función f(x) = cotg(2x) tampoco.
Sabemos que la función cotangente corta al eje X en: 0 = cotg(x) ⇔ x = π/2 ó x = 3π/2
En nuestro caso:
0 = cotg(2x) ⇔ 2x = π/2 ó 2x = 3π/2 ⇔ x = π/4 ó x = 3π/4
Como el período de nuestra función es π/2, los puntos de corte con el eje X en el primer período son:
(π/4 , 0) , (3π/4 , 0)
5) Máximos y mínimos:
La función cotangente no tiene máximos ni mínimos, por tanto, f(x) = cotg(2x) tampoco los tiene.
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
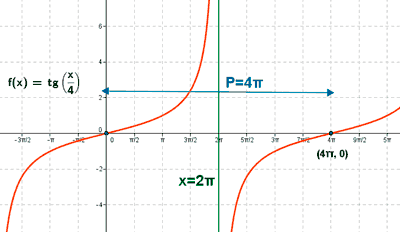
y = tg(x/4)
1) Dominio:
La función tangente no está definida en: (2k + 1)π/2 , k ∈ Z
Por tanto, nuestra función tampoco estará definida en:
x/4 = (2k + 1)π/2 k ∈ Z ⇔ x = 2(2k + 1)π , k ∈ Z
Luego: Dom(f) = R - { 2(2k + 1)π | k ∈ Z }
2) Recorrido: Im(f) = R
3) Periodicidad:
Como la función tangente es periódica de período π , la función f(x) = tg (x/4) es periódica de período:
x/4 = π ⇔ x = 4π
Es periódica de período 4π .
También podemos sacar el período de la función así:
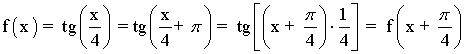
También podemos calcular el periodo de forma más fácil aplicando directamente la siguiente fórmula:
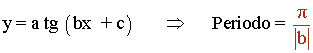
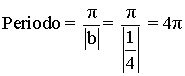
4) Puntos de corte:
Puntos de corte con el eje Y:
x = 0 ⇒ y = tg(x/4) ⇒ y = tg(0) ⇒ y = 0 ⇒ (0 , 0)
Sabemos que la función tangente corta al eje X en: 0 = tg(x) ⇔ x = 0 ó x = π
En nuestro caso: 0 = tg(x/4) ⇔ x = 0 ó x/4 = π ⇔ x = 0 ó x = 4π
Como el período de nuestra función es 4π , los puntos de corte con el eje X en el primer período son: (0 , 0) , (4π , 0)
5) Máximos y mínimos:
La función tangente no tiene máximos ni mínimos, por tanto, f(x) = tg(x/4) tampoco los tiene.
Dada la siguiente función, estudia todas sus características. Representa su gráfica.
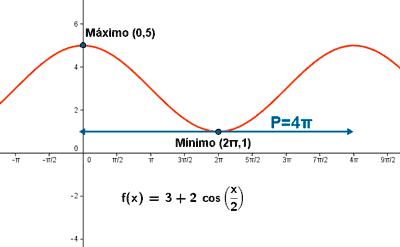
y = 3 + 2cos(x/2)
1) Dominio: Dom(f) = R
2) Recorrido:
Sabemos que el recorrido de la función coseno es [-1 , 1], por tanto el de cos(x/2) es también [-1 , 1] .
Es decir: - 1 ≤ cos(x/2) ≤ 1
Para obtener nuestra función en el miembro intermedio: multiplicamos por 2 y sumamos 3 unidades en cada miembro de la desigualdad.
- 1 ≤ cos(x/2) ≤ 1 ⇒ - 2 ≤ 2cos(x/2) ≤ 2
- 2 + 3 ≤ 3+ 2 cos(x/2) ≤ 2 + 3 ⇒ 1 ≤ 3+ 2 cos(x/2) ≤ 5
Luego: Im(f) = [1 , 5]
3) Periodicidad:
Sabemos que la función cos(x) es periódica de período 2π .
En nuestro caso: x/2 = 2π ⇔ x = 4π
Es periódica de período 4π .
También podemos sacar el período de la función así:
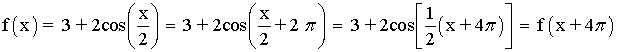
También podemos calcular el periodo de forma más fácil aplicando directamente la siguiente fórmula:
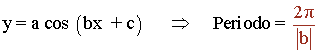
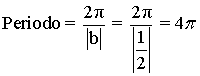
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 3 + 2 cos 0 ⇒ y = 3 + 2 = 5 ⇒ (0 , 5)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 3 + 2 cos(x/2) ⇒ cos(x/2) = -3/2
Pero sabemos que el recorrido de cos(x/2) es [-1 , 1] , es decir: -1 ≤ cos(x/2) ≤ 1
Sin embargo, -3/2 ∉ [-1 , 1]
Por tanto, no hay puntos de corte con el eje X.
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
5 = 3 + 2 cos(x/2) ⇒ 1 = cos(x/2) ⇒ x/2 = 0 ó x/2 = 2π
⇒ x = 0 ó x = 4π ⇒ (0 , 5) , (4π , 5)
Los puntos mínimos de la función vendrán dados por la ecuación:
1 = 3 + 2 cos(x/2) ⇒ -1 = cos(x/2) ⇒ x/2 = π ⇒ x = 2π ⇒ (2π , 1)
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
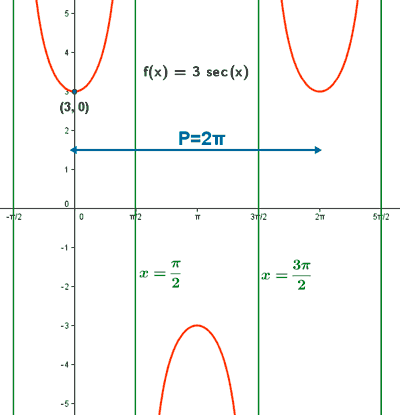
y = 3 sec(x)
1) Dominio:
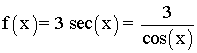
La función cos(x) es cero en:
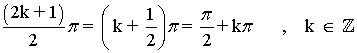
Por tanto, el dominio de nuestra función vendrá dado por:
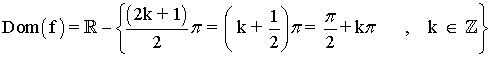
2) Recorrido:
Sabemos que el recorrido de la función coseno es [-1 , 1] . Es decir: - 1 ≤ cos(x) ≤ 1
Seperamos las dos desigualdades y, operando, tratamos de "conseguir" nuestra función:
![]()
Luego: - 3 ≥ f(x) , que representa el intervalo (-∞ , - 3]
![]()
Luego: f(x) ≥ 3 , que representa el intervalo [3 , ∞)
Por tanto, el recorrido o imagen de nuestra función es: Im(f) = (-∞ , - 3] ∪ [3 , ∞)
3) Periodicidad:
Como la función secante es periódica de período π , la función f(x) = 3 sec(x) tiene el mismo período: π .
También podemos sacar el período de la función así:
f(x) = 3 sec(x) = 3 sec(x + π) = f(x + π)
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 3 sec 0 ⇒ y = 3·1 = 3 ⇒ (0 , 3)
No tiene puntos de corte con el eje X, puesto que: y = 0 ∉ Im(f) = (-∞ , - 3] ∪ [3 , ∞)
5) Máximos y mínimos:
La función sec(x) no tiene ni máximos ni mínimos absolutos, por tanto, la función f(x) = 3 sec(x) tampoco.
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
y = - 3 + arc cos(x)
1) Dominio:
Sabemos que el dominio de la función arc cos(x) es [-1 , 1].
Por tanto, el de f(x) = - 3 + arc cos(x) es el mismo: Dom(f) = [-1 , 1] .
2) Recorrido:
Sabemos que el recorrido de la función arc cos(x) es [0 , π] .
Es decir: 0 ≤ arc cos(x) ≤ π
Para obtener nuestra función en el miembro intermedio: restamos 3 unidades en cada miembro de la desigualdad.
0 ≤ arc cos(x) ≤ π ⇒ - 3 ≤ - 3 + arc cos(x) ≤ π - 3 ⇒ - 3 ≤ f(x) ≤ π - 3
Por tanto: Im(f) = [ - 3 , π - 3]
3) Periodicidad:
Sabemos que la función arc cos(x) no tiene periodicidad, por tanto, la función f(x) = - 3 + arc cos(x) tampoco.
4) Puntos de corte:
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = -3 + arc cos 0 ⇒ y = - 3 + π/2 ⇒ (0 , - 3 + π/2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = -3 + arc cos (x) ⇒ arc cos(x) = 3 ⇒ x = cos 3 ⇒ ( cos 3 , 0)
5) Máximos y mínimos:
Sabemos que la función g(x) = arc cos(x) es decreciente.
Nuestra función es una traslación vertical hacia abajo de la función g , es decir:
f(x) = - 3 + arc cos(x) = - 3 + g(x)
Por tanto, nuestra función f también es decreciente.
Como Im(f) = [-3 , π - 3] , y f es decreciente, tenemos que:
• f tiene un mínimo absoluto en y = - 3 :
y = - 3 + arc cos(x) ⇒ - 3 = - 3 + arc cos(x) ⇒
⇒ 0 = arc cos(x) ⇒ cos 0 = x ⇒ x = 1 ⇒ (1 , -3)
• f tiene un máximo absoluto en y = π - 3 :
y = - 3 + arc cos(x) ⇒ π - 3 = - 3 + arc cos(x) ⇒
⇒ π = arc cos(x) ⇒ cos π = x ⇒ x = -1 ⇒ (-1 , π - 3)
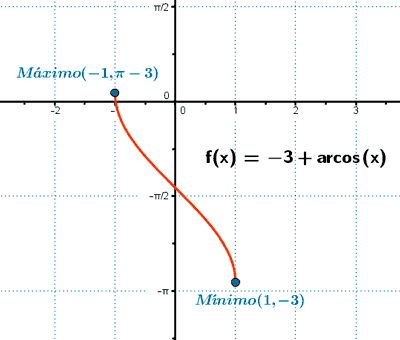
Dada la siguiente función, estudia todas sus características. Representa su gráfica.
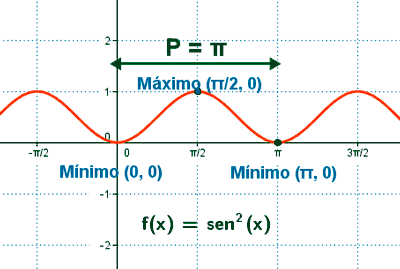
y = sen2(x)
1) Dominio:
El dominio de la función seno es todo R , por tanto, el dominio de nuestra función es el mismo:
Dom(f) = R
2) Recorrido:
Calcularemos su imagen o recorrido a través de su función invesa:
y = sen2(x) ⇒ ±√y = sen(x) ⇒ arcsen(±√y) = x
Intercambiamos las variables y estudiamos el dominio de la nueva función: y = arcsen(±√x)
• El dominio de la función arc sen(x) es: [-1 , 1]
• La raíz cuadrada está bien definida sólo en los números positivos: [0 , ∞)
Por tanto, su dominio es: [-1 , 1] ∩ [0 ,∞) = [0 , 1]
O lo que es lo mismo, la imagen de nuestra función es: Im(f) = [0 , 1]
3) Periodicidad:
Vamos a escribir f(x) de otra forma equivalente que nos permita calcular su período.
Usaremos la fórmula del coseno del ángulo doble: cos(2x) = cos2(x) - sen2(x)
Y también: 1 = cos2(x) + sen2(x)
cos(2x) = cos2(x) - sen2(x) ⇔ cos(2x) = (1 - sen2(x) ) - sen2(x) ⇔ cos(2x) = 1 - 2sen2(x) ⇔
⇔ 2sen2(x) = 1 - cos(2x) ⇔ sen2(x) = (1 - cos(2x) )/2
Ahora sí sabemos calcular su período teniendo en cuenta que el período de la función coseno es 2π :
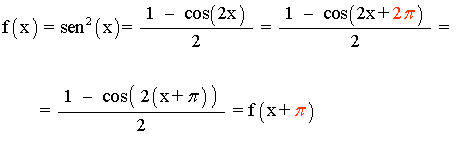
El período de f(x) es T = π .
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen2(0) ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen2(x) ⇒ 0 = ± sen(x) ⇒ x = 0 ó x = π
Luego los puntos de corte con el eje X son: (0 , 0) , (π , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
1 = sen2(x) ⇒ 1 = ± sen(x) ⇒ x = π/2 ⇒ (π/2 , 1)
Los puntos mínimos de la función vendrán dados por la ecuación:
0 = sen2(x) ⇒ 0 = ± sen(x) ⇒ x = 0 ó x = π ⇒ (0 , 0) , (π , 0)


 INICIO
INICIO