Problemas resueltos de aplicaciones de sistemas de ecuaciones II
• Problemas de empresas:
1) Un fabricante produce 42 electrodomésticos. La fábrica abastece a 3 tiendas, que demandan toda la producción. En una cierta semana, la primera tienda solicitó tantas unidades como la segunda y la tercera juntas, mientras que la segunda pidió un 20% más que la suma de la mitad de lo pedido por la primera más la tercera parte de lo pedido por la tercera. ¿Qué cantidad solicitó cada una?
2) Un pescadero compra el martes de una semana 96 kg de merluza y 130 kg de anchoas y paga por ello un total de 1.836 €. El lunes siguiente, el precio de la merluza ha subido un 20% y el de las anchoas un 30%. Ese dia compra 40 kg de merluza y 50 kg de anchoas, y paga un total de 918 €. ¿Hay datos suficientes para calcular el precio de la merluza y las anchoas el martes? Si la contestación es afirmativa calcula dichos precios, si es negativa razona por qué no se puede hacer dicho cálculo.
3) Una refinería compra petróleo a dos países A y B. Comprando 500 barriles al país A y 15.500 al país B resulta un precio medio de 19,875 euros. Comprando 1.000 barriles al país A y 1.000 al B el precio medio es de 18 euros por barril. ¿Cuánto cuesta el barrio de crudo de cada país?
4) En una tienda de ropa se liquidan los pantalones que han quedado sin vender en la temporada. Los hay de tres tipos:
- Sin defecto, todos al mismo precio de 20 euros
- Con defecto no apreciable, con una rebaja del 20% sobre el precio de los anteriores
- Con defecto apreciable, con una rebaja del 80% sobre el precio de los que no tienen defecto.
Hay 70 pantalones para vender. El precio total de todos ellos es de 1280 euros, y los que tienen defecto suponen el 40% de los que no lo tienen.
¿Cuántos pantalones hay de cada clase?
5) Una aseguradora tiene tres tarifas: una para adulto, otra para niño y otra para anciano. Se sabe que una familia de 3 adultos, 2 niños y 1 anciano paga 215 euros, una segunda familia de 4 adultos, 1 niño y 2 ancianos paga 260, una tercera familia de 2 adultos, 2 niños y 1 anciano paga 190 euros.
a) ¿Cuánto paga cada niño, adulto y anciano?
b) ¿Cuánto pagará una familia de 5 adultos, 3 niños y 2 ancianos?
6) Una empresa cinematográfica dispone de tres cines C1, C2 y C3. Cierto día, en cada uno de ellos, proyecta tres películas P1, P2 y P3 (P1 es en sesión de mañana, P2 en sesión de tarde y P3 en sesión de noche). El número de asistentes, (expresado en centenas), a cada una de ellas se indica en la siguiente tabla:
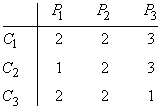
Sabiendo que los ingresos obtenidos en ese día en C1, C2 y C3, fueron de 900 euros, 840 euros y 540 euros respectivamente, calcular el precio de la entrada para cada una de las tres películas.
7) Una empresa ha invertido 73.000 € en la compra de ordenadores portátiles de tres clases A, B y C, cuyos costes por unidad son de 2.400 €, 1.200 € y 1.000 € respectivamente. Sabiendo que, en total, ha adquirido 55 ordenadores y que la cantidad invertida en los de tipo A ha sido la misma que la invertida en los de tipo B, averiguar cuántos aparatos ha comprado de cada clase.
8) En un hotel hay un total de 240 turistas ingleses, alemanes y franceses. Si los franceses son la mitad de la suma de alemanes e ingleses y el 200% de los ingleses igualan a la suma de alemanes y franceses:
a) Plantear el correspondiente sistema de ecuaciones
b) Determinar cuántos turistas de cada nacionalidad hay en el hotel
• Problemas con parámetros:
9) De tres números x, y, z sabemos que el primero más el segundo suman cero; el primero más el tercero suman uno; la suma de los tres vale cero; y el primero multiplicado por un número k más el doble de la suma del segundo y el tercero es uno.
a) ¿Qué puedes decir del valor de k ?
b) ¿Cuánto vale cada uno de los números?
10) Una persona ha obtenido 6000 € de beneficio por invertir un total de 60 000€ en tres empresas A, B y C. La suma del dinero invertido en A y B fue m veces el invertido en C y los beneficios fueron el 5% en A el 10% en B y el 20% en C.
- Plantea un sistema de ecuaciones para averiguar la cantidad invertida en cada empresa.
- Prueba que si m > 0, el sistema es compatible determinado.
- Halla la solución del sistema para m = 5.
11) Las edades, en años, de un niño, su padre y su abuelo verifican las siguientes condiciones:
• La edad del padre es a veces la de su hijo
• El doble de la edad del abuelo más la edad del niño y más la del padre es de 182 años
• El doble de la edad del niño más la del abuelo es 100
a) Establece las edades de los tres suponiendo que a = 2
b) Para a = 3, ¿qué ocurre con el problema planteado?
c) Siguiendo con a = 3, ¿qué ocurre si en la segunda condición la suma es de 200 en vez de 182?
Problemas resueltos de aplicaciones de sistemas de ecuaciones I
1) Un fabricante produce 42 electrodomésticos. La fábrica abastece a 3 tiendas, que demandan toda la producción. En una cierta semana, la primera tienda solicitó tantas unidades como la segunda y la tercera juntas, mientras que la segunda pidió un 20% más que la suma de la mitad de lo pedido por la primera más la tercera parte de lo pedido por la tercera. ¿Qué cantidad solicitó cada una?
Vamos a llamar x a la cantidad que solicitó la primera tienda, y a la que solicitó la segunda tienda y z a la que solicitó la tercera tienda. Y a continuación traducimos el enunciado a lenguaje algebráico:
- Las tres tiendas demandan 42 electrodomésticos.
x + y + z = 42
- La primera tienda solicitó tantas unidades como la segunda y la tercera juntas.
x = y + z
- La segunda tienda pidió un 20% más que la suma de la mitad de la primera tienda más la tercera parte de la tercera tienda.
![]()
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
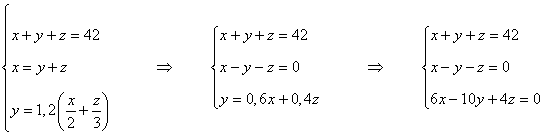
Aplicamos Gauss:
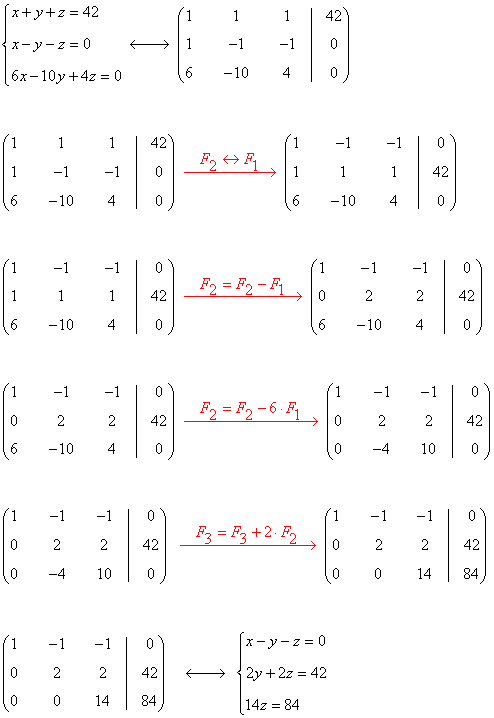
Resolvemos el sistema equivalente:
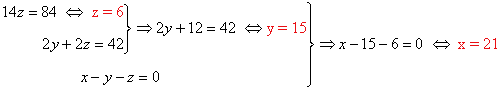
Solución:
La primera tienda solicitó 21 electrodomésticos, la segunda tienda solicitó 15 electrodomésticos y la tercera tienda solicitó 6 electrodomésticos.
2) Un pescadero compra el martes de una semana 96 kg de merluza y 130 kg de anchoas y paga por ello un total de 1.836 €. El lunes siguiente, el precio de la merluza ha subido un 20% y el de las anchoas un 30%. Ese dia compra 40 kg de merluza y 50 kg de anchoas, y paga un total de 918 €. ¿Hay datos suficientes para calcular el precio de la merluza y las anchoas el martes? Si la contestación es afirmativa calcula dichos precios, si es negativa razona por qué no se puede hacer dicho cálculo.
Vamos a llamar x al precio de la merluza e y al precio de las anchoas. Y a continuación traducimos el enunciado a lenguaje algebráico:
- El martes compra 96 kg de merluza y 130 de anchoas y paga 1.836 €.
96x + 130y = 1.836
- El miercoles la merluza ha subido un 10% y la anchoa un 30%, compra 40 kg de merluza y 50 kg de anchoas y paga 918 €.
40·1,2x + 50·1,3y = 918
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
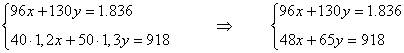
Aplicamos Gauss:
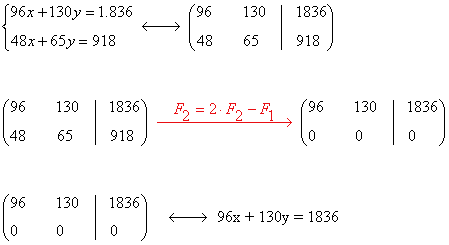
Llegamos a una ecuación con dos incógnitas, por lo que el sistema es compatible indeterminado, es decir, tiene infinitas soluciones. Por lo tanto, no se pueden hallar los precios que nos pide el problema.
3) Una refinería compra petróleo a dos países A y B. Comprando 500 barriles al país A y 15.500 al país B resulta un precio medio de 19,875 euros. Comprando 1.000 barriles al país A y 1.000 al B el precio medio es de 18 euros por barril. ¿Cuánto cuesta el barrio de crudo de cada país?
Vamos a llamar x al precio del barril del país A e y al precio del país B. Y a continuación traducimos el enunciado a lenguaje algebráico:
- Comprando 500 barriles al país A y 15.500 al país B resulta un precio medio de 19,875 euros.
500x + 15.500y = (500 + 15.500)·19,875
- Comprando 1.000 barriles al país A y 1.000 al B el precio medio es de 18 euros por barril.
1.000x + 1.000y = (1.000 + 1.000)·18
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
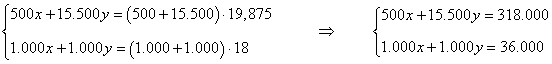
Aplicamos Gauss:
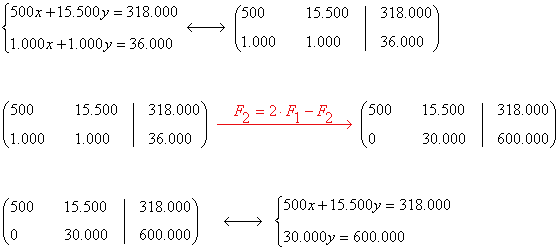
Resolvemos el sistema equivalente:
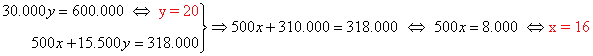
Solución:
En el país A cuesta el barril 16 euros y en el país B 20 euros.
4) En una tienda de ropa se liquidan los pantalones que han quedado sin vender en la temporada. Los hay de tres tipos:
- Sin defecto, todos al mismo precio de 20 euros
- Con defecto no apreciable, con una rebaja del 20% sobre el precio de los anteriores
- Con defecto apreciable, con una rebaja del 80% sobre el precio de los que no tienen defecto.
Hay 70 pantalones para vender. El precio total de todos ellos es de 1280 euros, y los que tienen defecto suponen el 40% de los que no lo tienen.
¿Cuántos pantalones hay de cada clase?
Vamos a llamar x a la cantidad de pantalones sin defecto, y a los que tienen defecto no apreciable y z a los que tienen defecto apreciable. Y a continuación traducimos el enunciado a lenguaje algebráico:
- Hay 70 pantalones para vender.
x + y + z = 70
- El precio total de todos ellos es de 1.280 euros.
20x + 16y + 8z = 1.280
- Los que tienen defectos suponen el 40% de los que no lo tienen.
![]()
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
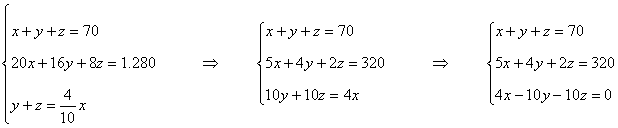
Aplicamos Gauss:
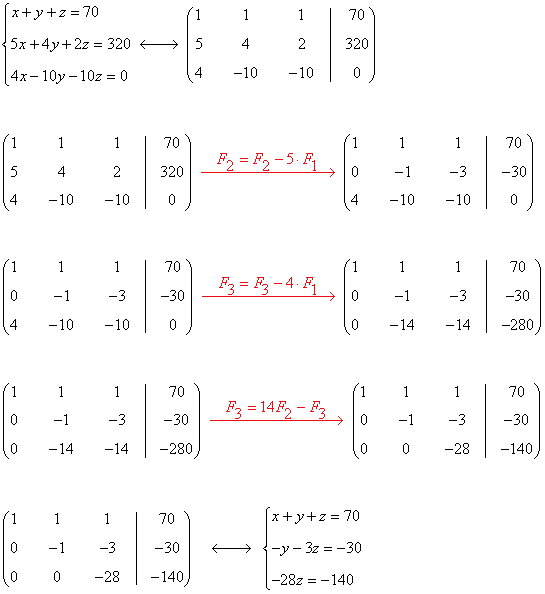
Resolvemos el sistema equivalente:
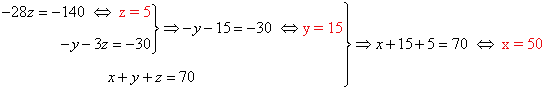
Solución:
Hay 50 pantalones sin defecto, 15 con defecto no apreciable y 5 con defecto apreciable.
5) Una aseguradora tiene tres tarifas: una para adulto, otra para niño y otra para anciano. Se sabe que una familia de 3 adultos, 2 niños y 1 anciano paga 215 euros, una segunda familia de 4 adultos, 1 niño y 2 ancianos paga 260, una tercera familia de 2 adultos, 2 niños y 1 anciano paga 190 euros.
a) ¿Cuánto paga cada niño, adulto y anciano?
b) ¿Cuánto pagará una familia de 5 adultos, 3 niños y 2 ancianos?
Vamos a llamar x a la tarifa de adulto, y a la tarifa de niño y z a la tarifa de anciano. Y a continuación traducimos el enunciado a lenguaje algebráico:
- Una familia de 3 adultos, 2 niños y 1 anciano paga 215 euros.
3x + 2y + z = 215
- Una familia de 4 adultos, 1 niño y 2 ancianos paga 260 euros.
4x + y + 2z = 260
- Una familia de 2 adultos, 2 niños y 1 anciano paga 190 euros.
2x + 2y + z = 190
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
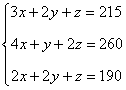
Aplicamos Gauss:
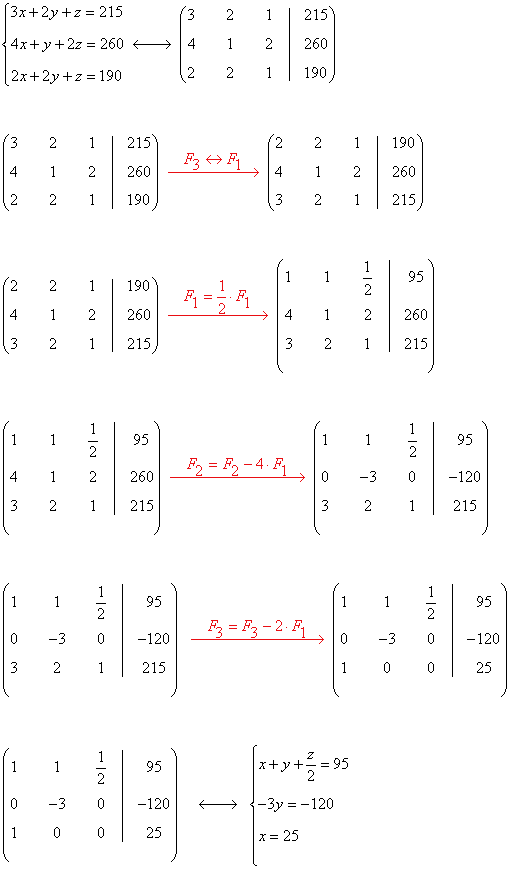
Resolvemos el sistema equivalente:
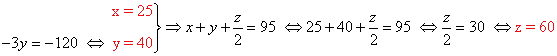
Solución:
• La tarifa de adulto es de 25 euros, la tarifa de niño de 40 euros y la tarifa de anciano de 60 euros.
• Una familia con 5 adultos, 3 niños y 2 ancianos pagaría: 5·25 + 3·40 + 2·60 = 365 euros
6) Una empresa cinematográfica dispone de tres cines C1, C2 y C3. Cierto día, en cada uno de ellos, proyecta tres películas P1, P2 y P3 (P1 es en sesión de mañana, P2 en sesión de tarde y P3 en sesión de noche). El número de asistentes, (expresado en centenas), a cada una de ellas se indica en la siguiente tabla:
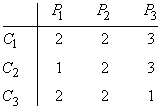
Sabiendo que los ingresos obtenidos en ese día en C1, C2 y C3, fueron de 900 euros, 840 euros y 540 euros respectivamente, calcular el precio de la entrada para cada una de las tres películas.
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar.
x → precio película P1 y → precio película P2 z → precio película P3
De la tabla y las condiciones, obtenemos el siguiente sistema de ecuaciones:
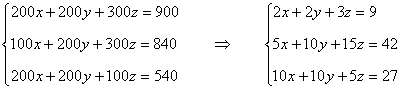
Aplicamos Gauss:

Resolvemos el sistema equivalente:
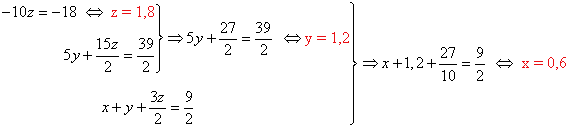
Solución:
P1 cuesta 0,6 euros, P2 cuesta 1,2 euros y P3cuesta 1,8 euros.
7) Una empresa ha invertido 73.000 € en la compra de ordenadores portátiles de tres clases A, B y C, cuyos costes por unidad son de 2.400 €, 1.200 € y 1.000 € respectivamente. Sabiendo que, en total, ha adquirido 55 ordenadores y que la cantidad invertida en los de tipo A ha sido la misma que la invertida en los de tipo B, averiguar cuántos aparatos ha comprado de cada clase.
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar.
x → ordenador clase A y → ordenador clase B z → ordenador clase C.
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
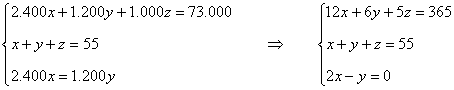
Aplicamos Gauss:
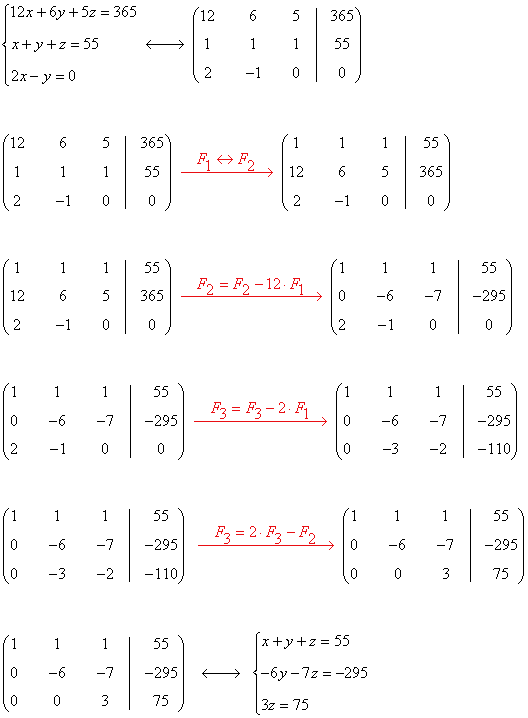
Resolvemos el sistema equivalente:
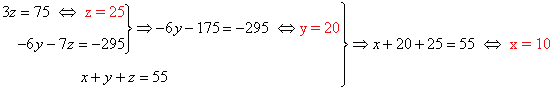
Solución:
La empresa ha comprado 10 ordenadores de clase A, 20 de clase B y 25 de clase C.
8) En un hotel hay un total de 240 turistas ingleses, alemanes y franceses. Si los franceses son la mitad de la suma de alemanes e ingleses y el 200% de los ingleses igualan a la suma de alemanes y franceses:
a) Plantear el correspondiente sistema de ecuaciones
b) Determinar cuántos turistas de cada nacionalidad hay en el hotel
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar.
x → turistas ingleses y → turistas alemanes z → turistas franceses
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
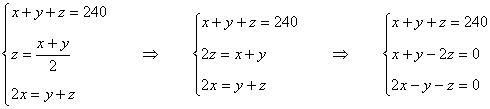
Aplicamos Gauss:
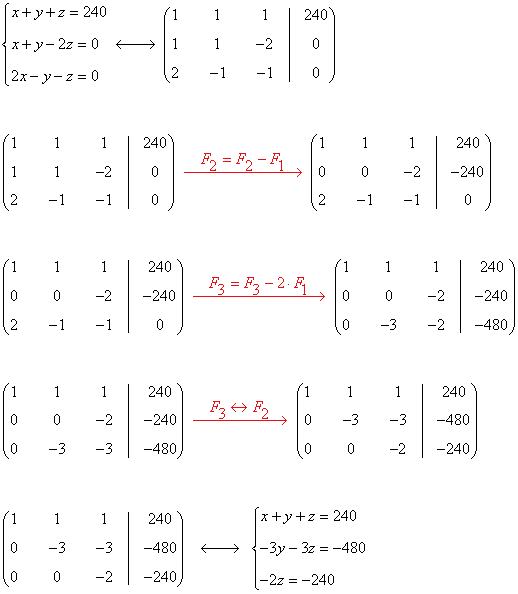
Resolvemos el sistema equivalente:
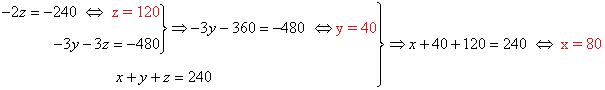
Solución:
Hay 80 ingleses, 40 alemanes y 120 franceses.
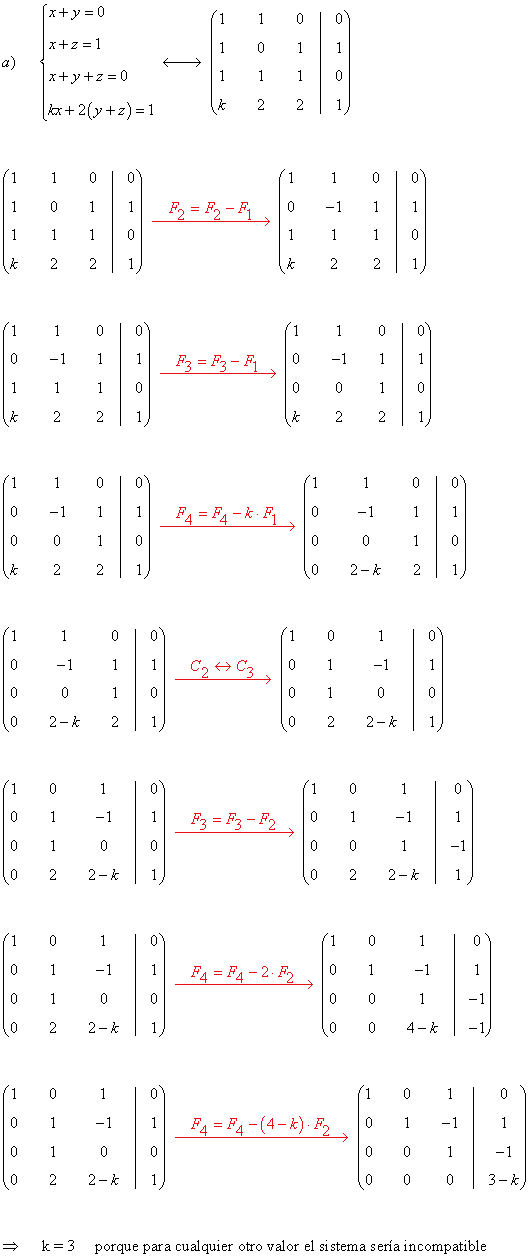
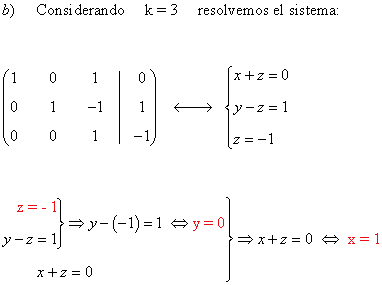
9) De tres números x, y, z sabemos que el primero más el segundo suman cero; el primero más el tercero suman uno; la suma de los tres vale cero; y el primero multiplicado por un número k más el doble de la suma del segundo y el tercero es uno.
a) ¿Qué puedes decir del valor de k ?
b) ¿Cuánto vale cada uno de los números?
10) Una persona ha obtenido 6000 € de beneficio por invertir un total de 60 000€ en tres empresas A, B y C. La suma del dinero invertido en A y B fue m veces el invertido en C y los beneficios fueron el 5% en A el 10% en B y el 20% en C.
- Plantea un sistema de ecuaciones para averiguar la cantidad invertida en cada empresa.
- Prueba que si m > 0, el sistema es compatible determinado.
- Halla la solución del sistema para m = 5.
1.-
Llamamos
x → cantidad invertida en A y → cantidad invertida en B z → cantidad invertida en C
Nos dicen que la persona ha invertido un total de 60 000 euros en las tres empresas. Algebraicamente esto se expresa como
x + y + z = 60000
Por otra parte, nos dicen que la suma del dinero invertido en A y B es m veces el dinero invertido en C. Esto es expresa algebraicamente de la siguiente forma:
x + y = mz
Observamos además que debe tenerse m>0 ya que si no, la ecuación no tendría sentido.
Finalmente, los beneficios totales fueron de 6000€: el 5% de beneficios en A el 10% en B y el 20% en C. La ecuación lineal que nos permite expresar esto es la siguiente:
0,05x + 0,10y + 0,20z = 6000
Reuniendo las tres ecuaciones obtenemos el sistema que se nos pide en el primer apartado:
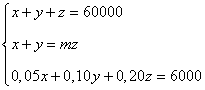
2.-
Aplicamos Gauss:

El sistema es incompatible determinado si m=-1 y compatible determinado en los demás casos. Por tanto si m>0 el sistema es compatible determinado.
3.-
Resolvemos el sistema para m = 5. Aprovechando. El trabajo que hemos hecho en el apartado anterior, bastará con resolver el sistema equivalente a la última matriz para m = 5:
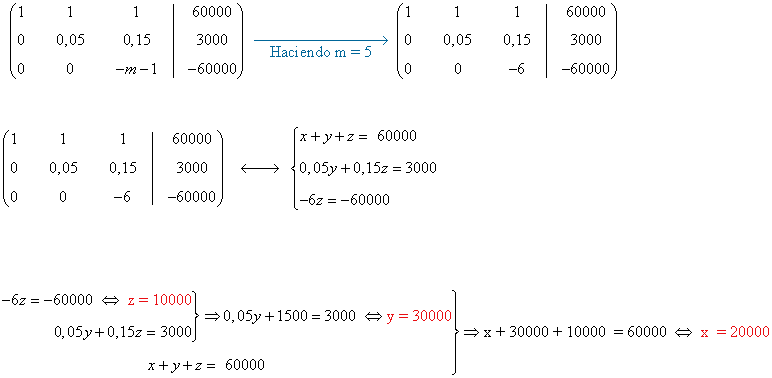
de manera que para m = 5 obtenemos que la inversión fue de 20 000 € en la empresa A, 30 000 € en la empresa B y 10 000 € en la empresa C.
11) Las edades, en años, de un niño, su padre y su abuelo verifican las siguientes condiciones:
• La edad del padre es a veces la de su hijo
• El doble de la edad del abuelo más la edad del niño y más la del padre es de 182 años
• El doble de la edad del niño más la del abuelo es 100
a) Establece las edades de los tres suponiendo que a = 2
b) Para a = 3, ¿qué ocurre con el problema planteado?
c) Siguiendo con a = 3, ¿qué ocurre si en la segunda condición la suma es de 200 en vez de 182?
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
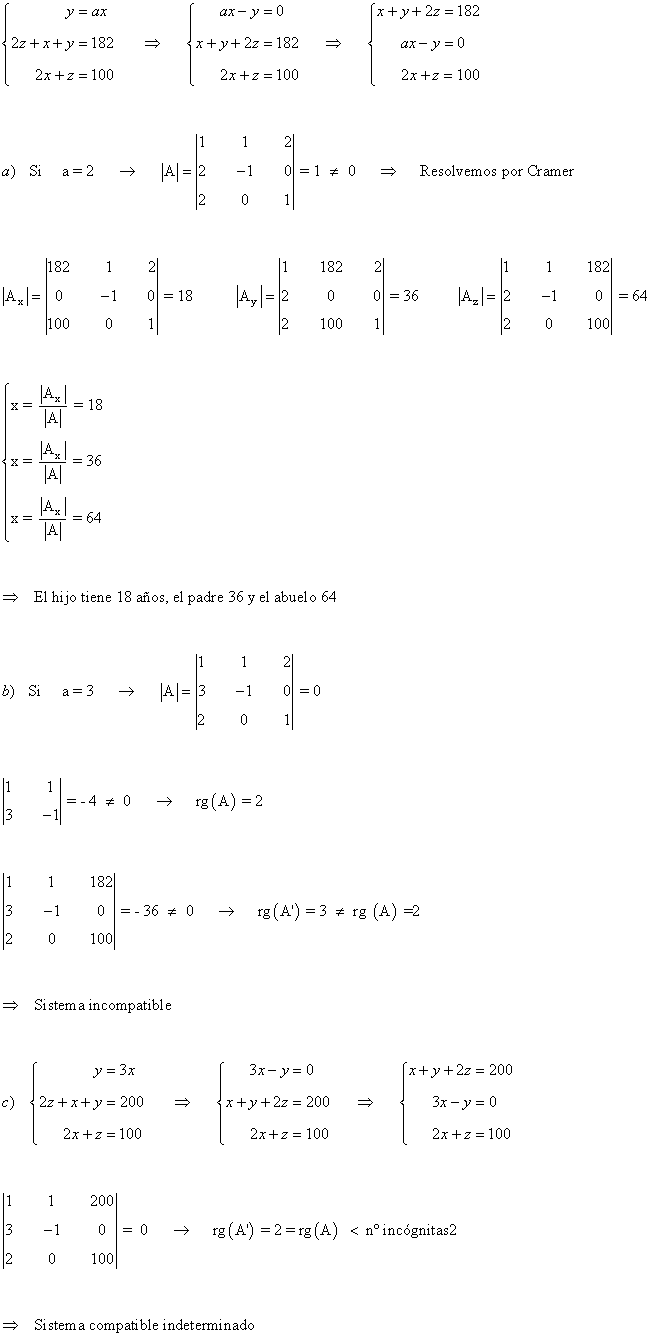


 INICIO
INICIO