Ecuaciones lineales
Ecuaciones lineales con dos incógnitas
Se llama ecuación lineal con 2 incógnitas, x , y a toda expresión del tipo
![]()
donde los números reales a, b son los coeficientes y el número real c el término independiente.
Ejemplo de ecuación lineal con dos incógnitas
La ecuación lineal con dos incógnitas -2x - 3y = -6, que es una recta cuya gráfica mostramos a continuación, tiene infinitas soluciones.
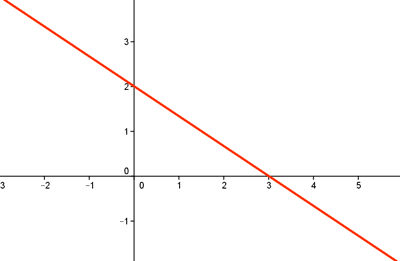
Para cada valor que se dé a la incógnita x, existirá un único valor de la incógnita y, es decir, si x=0, entonces y=2, si x= 3 entonces y = 0...
En general, si tomamos x = λ, entonces
![]()
de manera que las soluciones de la ecuación tendrán todas la forma
![]()
Ecuaciones lineales con tres incógnitas
Se llama ecuación lineal con 3 incógnitas, x , y, z a toda expresión del tipo
![]()
donde los números reales a, b, c son los coeficientes y el número real d el término independiente.
Ejemplo de ecuación lineal con tres incógnitas
La ecuación lineal con tres incógnitas x + y - 3z = 5, cuya gráfica es un plano, tiene infinitas soluciones.
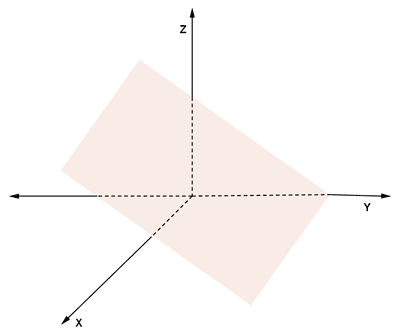
Para cada par de valores que se dé a las incógnitas y, z , existirá un único valor de la incógnita x, es decir:
- Si z = 0 , y = 1 , entonces x = 4.
- Si z = 1 , y = 0 , entonces x = 8 ...
En general, si tomamos z = λ, y = μ, entonces
![]()
de manera que las soluciones de la ecuación tendrán todas la forma
![]()
Ecuaciones lineales con n incógnitas
Se llama ecuación lineal con n incógnitas, x1, x2, x3, ..., xn a toda expresión del tipo
![]()
donde los números reales a1, a2, a3, ..., an son los coeficientes y el número real b el término independiente.
Si b = 0, la ecuación recibe el nombre de homogénea.
Ejemplo de ecuación lineal con tres incógnitas
La ecuación lineal con cuatro incógnitas x + y - 3z + w = 5, tiene infinitas soluciones.
Para cada par de valores que se dé a las incógnitas y, z , w existirá un único valor de la incógnita x, es decir:
- Si z = 0 , y = 1 , w= 0 entonces x = 4.
- Si z = 1 , y = 0 , w= 0 entonces x = 8 ...
En general, si tomamos z = λ, y = μ, w = γ, entonces
![]()
de manera que las soluciones de la ecuación tendrán todas la forma
![]()
Decimos que dos ecuaciones lineales son equivalentes cuando tienen las mismas soluciones.
Para obtener una ecuación equivalente a una ecuación F dada hay que
Multiplicarla por un número real k distinto de cero: F → k F
Ejemplos de ecuaciones equivalentes
Consideremos las ecuaciones
x + y = 2,
2x +2y = 4
Las ecuaciones son equivalentes ya que la segunda ecuación es el resultado de multiplicar la primera por dos.


 INICIO
INICIO
