Sistemas de ecuaciones lineales
Un sistema con m ecuaciones y n incógnitas es conjunto de ecuaciones lineales de la forma:
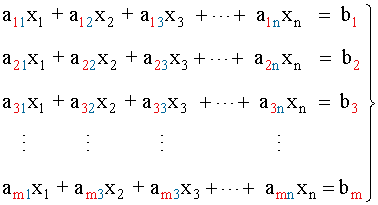
Donde los números reales a11, a12, ... , amn son los coeficientes, x1, x2, x3, ..., xn son las incógnitas y los números reales b1, b2, b3, ..., bn son los términos independientes.
Ejemplos de sistemas de ecuaciones lineales
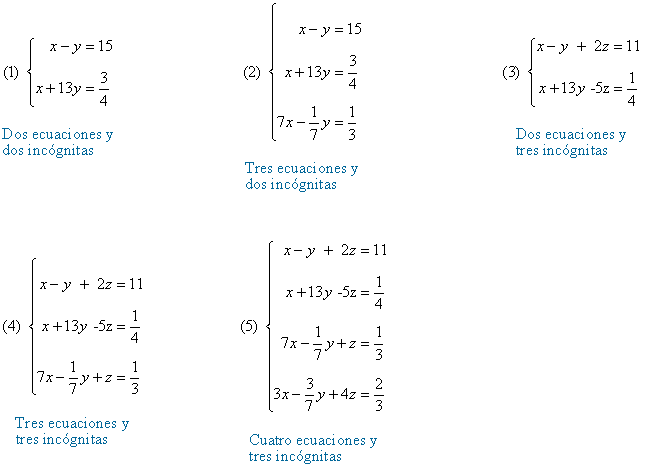
Resolver un sistema de ecuaciones es hallar, si existen, los valores de las incógnitas que verifiquen simultaneamente todas las ecuaciones del sistema.
Ejemplo de solución de un sistema

Sistemas de ecuaciones equivalentes
Decimos que dos sistemas de ecuaciones son equivalentes si tienen la misma solución.
Para pasar de un sistema de ecuaciones a otro equivalente podemos realizar sobre sus ecuaciones F1, F2, ... , Fn las siguientes operaciones:
- Cambiar el orden de las ecuaciones: Fi ↔ Fj
- Multiplicar una o más ecuaciones por un número real distinto de cero: Fi → k Fj
- Sumar a una ecuación otra multiplicada por un número real: Fi → Fi + k Fj
Ilustramos esto con un ejemplo:
Ejemplos de sistemas equivalentes
Dado el siguiente sistema de ecuaciones
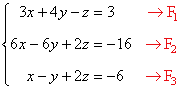
Calcular los siguientes sistemas equivalentes:
- El obtenido al multiplicar por 3 la segunda ecuación.
- El obtenido al sumar el doble de la tercera ecuación a la primera.
- El que se obtiene al intercambiar la primera y la tercera ecuación.
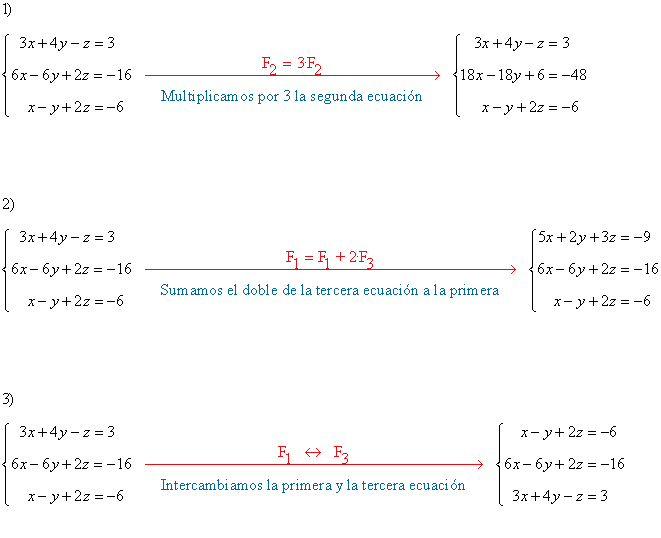
Puede comprobarse que los sistemas obtenidos tienen todos la misma solución que el original:
x = -1 y = 1 z = 2
o en forma de terna ( x , y , z ) = ( -1 , 1 , 2 ).


 INICIO
INICIO

