Aplicaciones de los sistemas de ecuaciones

Problema de cifras

Halla un número de tres cifras sabiendo que estas suman 9; que si al número dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198, y que la cifra de las decenas es la media aritmética de las otras dos.

Vamos a seguir los pasos que hemos expuesto antes.

1. Traducir al lenguaje algebraico el enunciado:

   Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar. Llamamos
   x → unidades        y → decenas       z → centenas

   Nos dicen que estas cifras suman 9, es decir
   x + y + z = 9

   Que si al número dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198, es decir,
   100z + 10y + x - (100x + 10y + z) = 198

   y que la cifra de las decenas es la media aritmética de las otras dos, es decir,
   

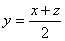
   Reuniendo las tres ecuaciones el número que queremos determinar será el que tenga por cifras a las soluciones del siguiente sistema de ecuaciones:
   
   
   

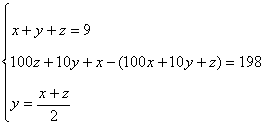
2. Calcular las soluciones empleando las herramientas algebraicas:

   

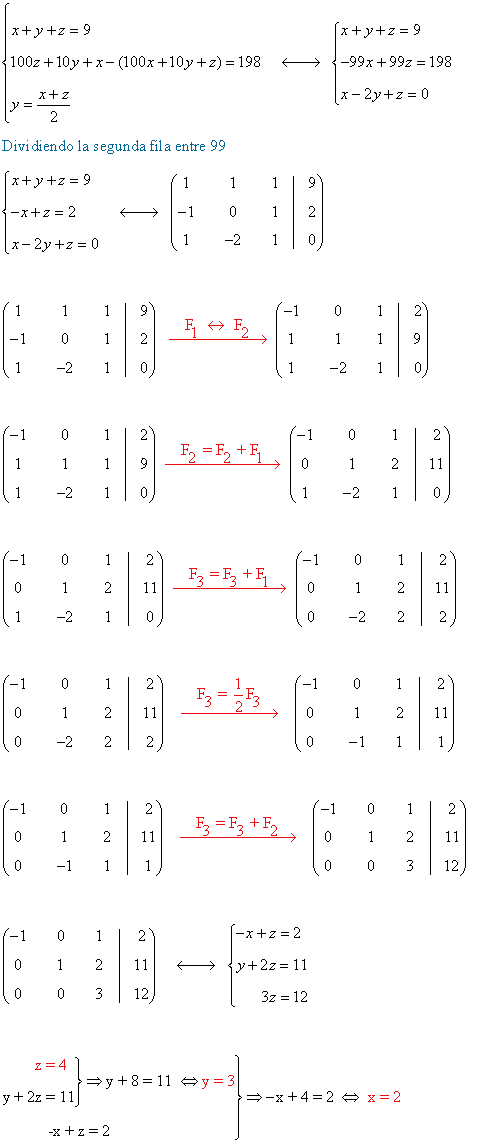
3. Comprobar las soluciones obtenidas:

Esta solución tiene sentido, ya que se nos pedía determinar las cifras de un número de tres cifras y dichas cifras deben ser números naturales entre 0 y 9.

El número que queríamos determinar es el 432.

Problema de edades

La edad de un padre es el doble de la suma de las edades de sus dos hijos, mientras que hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era el triple que la suma de las edades en aquel tiempo de sus hijos. Cuando pasen tantos años como la suma de las edades actuales de los hijos, entre los tres sumarán 150 años. ¿Qué edad tenía el padre cuando nacieron sus hijos?

Vamos a hacer una tabla que nos va a facilitar traducir al álgebra el problema que nos plantean:

	Edad actual	Edad hace y - z años	Edad dentro de y + z años
Padre	x	x - (y - z) = x - y + z	x + (y+z) = x + y + z
Primer hijo	y	y - (y - z) = z	y + (y + z) = 2y + z
Segundo hijo	z	z - (y - z) = -y + 2z	z + (y + z) = y + 2z

Teniendo en cuenta esta tabla es fácil obtener las ecuaciones que nos permiten resolver el problema:

• La edad de un padre es el doble de la suma de las edades de sus dos hijos: En este caso se nos habla de edad actual. Nos fijamos en la columna de edades actuales. La ecuación sería la siguiente:
  
  

  

• Hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era el triple que la suma de las edades en aquel tiempo de sus hijos: En este caso nos fijamos en las respectivas edades que vienen dadas por la segunda columna. La ecuación sería la siguiente:
  
  

  

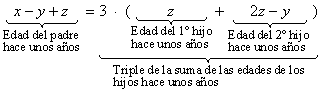
• Cuando pasen tantos años como la suma de las edades actuales de los hijos, entre los tres sumarán 150 años: En este caso consideramos la información de la tercera columna de la matriz. La ecuación que obtenemos es la siguiente:
  
  

  

Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:

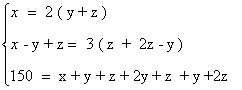
Aplicamos Gauss:

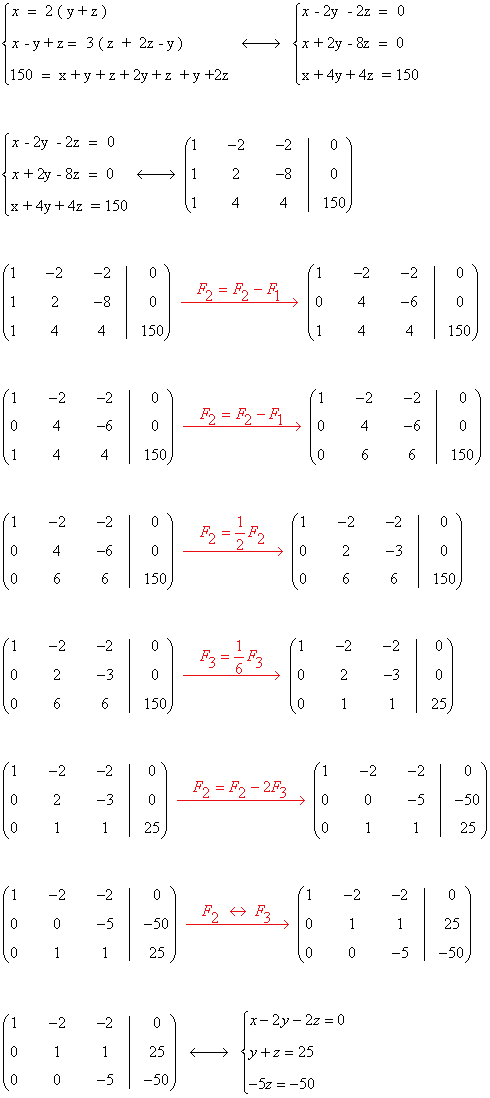
Resolvemos el sistema equivalente:

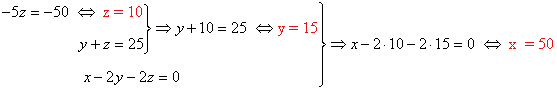
Actualmente el padre tiene 50 años, el primer hijo 15 y el segundo hijo 10.

La solución del sistema no es la respuesta a la pregunta que nos plantea el problema ya que nos piden la edad del padre cuando nacieron cada uno de sus hijos. La respuesta sería la siguiente:

• El padre tenía 35 años cuando nació su primer hijo, ya que actualmente tiene 50 años y el primer hijo nació hace 15.
• El padre tenía 40 cuando nació el segundo hijo, ya que actualmente tiene 50 años y su segundo hijo nació hace 10.

Problema de empresas (sistema con parámetro)

Una persona ha obtenido 6000 € de beneficio por invertir un total de 60 000€ en tres empresas A, B y C. La suma del dinero invertido en A y B fue m veces el invertido en C y los beneficios fueron el 5% en A el 10% en B y el 20% en C.

1. Plantea un sistema de ecuaciones para averiguar la cantidad invertida en cada empresa.
2. Prueba que si m > 0, el sistema es compatible determinado.
3. Halla la solución del sistema para m = 5.

1.-

Llamamos

x → cantidad invertida en A          y → cantidad invertida en B          z → cantidad invertida en C

Nos dicen que la persona ha invertido un total de 60 000 euros en las tres empresas. Algebraicamente esto se expresa como

x + y + z = 60000

Por otra parte, nos dicen que la suma del dinero invertido en A y B es m veces el dinero invertido en C. Esto es expresa algebraicamente de la siguiente forma:

x + y = mz

Observamos además que debe tenerse m>0 ya que si no, la ecuación no tendría sentido.

Finalmente, los beneficios totales fueron de 6000€: el 5% de beneficios en A el 10% en B y el 20% en C. La ecuación lineal que nos permite expresar esto es la siguiente:

0,05x + 0,10y + 0,20z = 6000

Reuniendo las tres ecuaciones obtenemos el sistema que se nos pide en el primer apartado:

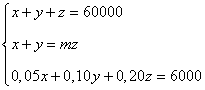
2.-

Aplicamos Gauss:

El sistema es incompatible determinado si m=-1 y compatible determinado en los demás casos. Por tanto si m>0 el sistema es compatible determinado.

3.-

Resolvemos el sistema para m = 5. Aprovechando. El trabajo que hemos hecho en el apartado anterior, bastará con resolver el sistema equivalente a la última matriz para m = 5:

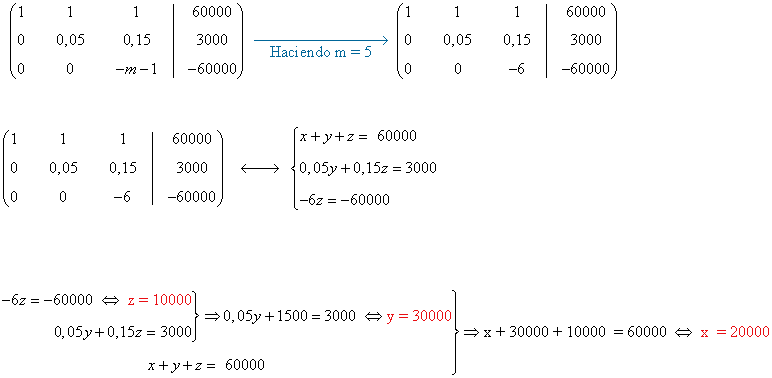
de manera que para m = 5 obtenemos que la inversión fue de 20 000 € en la empresa A, 30 000 € en la empresa B y 10 000 € en la empresa C.