Resolución de sistemas de ecuaciones por el método de Gauss
Sistemas de ecuaciones escalonados
Un sistema de ecuaciones lineales es escalonado si tiene la forma:
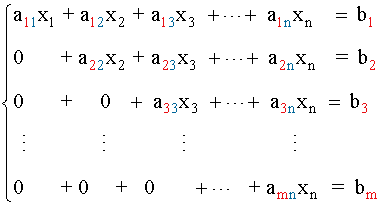
Sistemas de ecuaciones triangulares
Los sistemas de ecuaciones escalonados que tienen el mismo número de ecuaciones que de incógnitas reciben el nombre de sistemas escalonados triangulares.
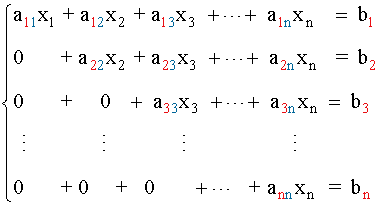
Ejemplo de resolución de sistema escalonado triangular
Resolver el siguiente sistema escalonado triangular:
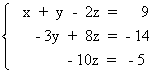
Para resolver este tipo de sistemas, empezamos resolviendo la última ecuación. Después sustituimos el valor de la última incógnita en la ecuación anterior, y así sucesivamente.
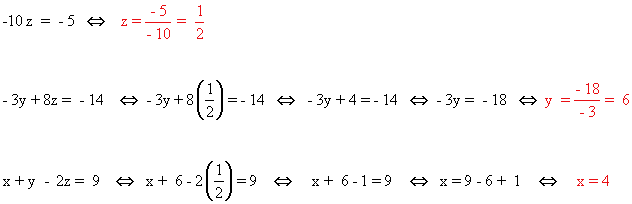
Método de Gauss
El método de Gauss, nos permite pasar de un sistema de ecuaciones lineales a otro sistema de ecuaciones lineales equivalente al anterior y además escalonado (o escalonado triangular).
El método de Gauss consiste en aplicar reiteradamente las siguientes operaciones:
- Cambiar el orden de las ecuaciones: Fi ↔ Fj
- Multiplicar una o más ecuaciones por un número real distinto de cero: Fi → k Fj
- Sumar a una ecuación otra multiplicada por un número real: Fi → Fi + k Fj
Hasta obtener un sistema escalonado (o escalonado triangular).
Ejemplo de resolución de sistema de ecuaciones por el método de Gauss
Resolver el siguiente sistema de ecuaciones por el método de Gauss:
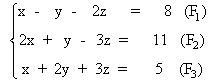
Primero obtenemos un sistema escalonado triangular:
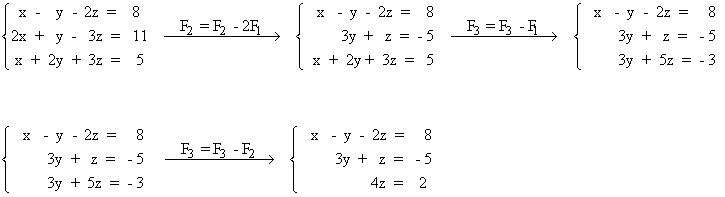
Después resolvemos el sistema triangular:
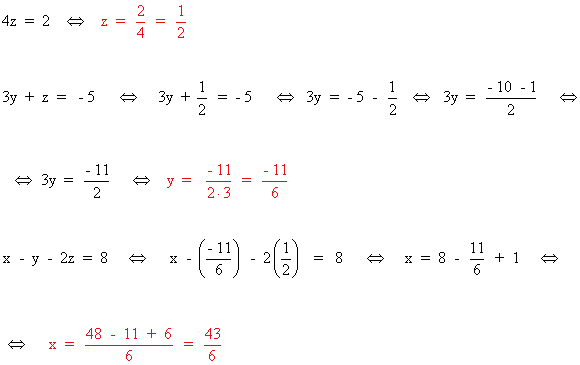
Notación matricial de un sistema de ecuaciones
Una matriz puede entenderse como una "tabla ordenada de números escritos en filas y columnas"

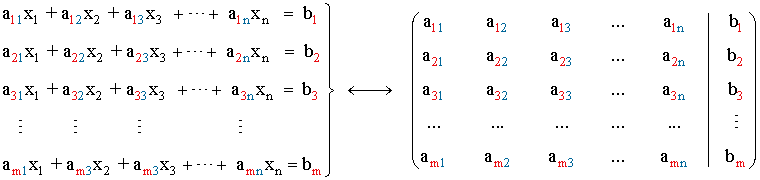
A cada sistema de ecuaciones lineales podemos hacerle corresponder una matriz ampliada de la siguiente forma:
Operando de igual forma que con las ecuaciones, podemos trabajar con las filas de la matriz asociada.
Ejemplo del método de Gauss con notación matricial
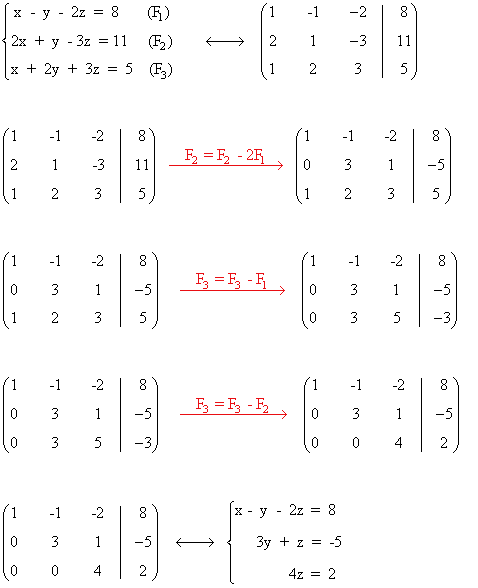
y el resto del problema se haría como antes:
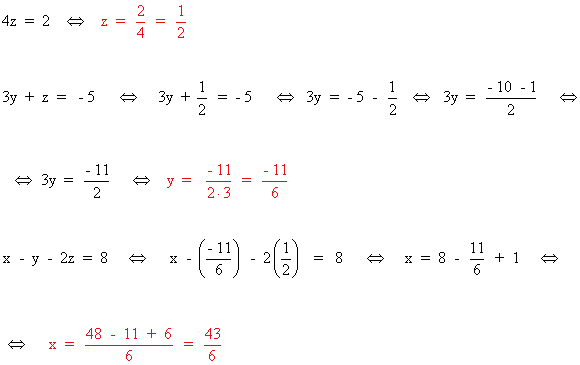


 INICIO
INICIO

