Ejercicios resueltos de ecuaciones racionales
No confundir:

Ejercicios de ecuaciones racionales de primer grado:
![]()
![]()
![]()
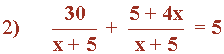
1. Se suprimen los denominadores. Se halla el m.c.m. de los denominadores de ambos miembros:
m.c.m. (x + 5, x + 5, 1) = x + 5
Dividimos el mínimo común multiplo (m.c.m.) por
cada denominador y multiplicamos por su numerador, en ambos miembros.
30 + 5 + 4x = 5(x + 5)
30 + 5 + 4x = 5x + 25
2. Se hace la transposición de términos.
4x - 5x = 25 - 30 - 5
3. Se reducen los términos semejantes.
- x = - 10
4. Se despeja la incógnita.
x = 10
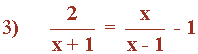
1. Se suprimen los denominadores. Se halla el m.c.m. de los denominadores de ambos miembros:
m.c.m.( x + 1, x - 1, 1 ) = (x + 1)(x - 1) = x2 - 1
Dividimos el mínimo común multiplo (m.c.m.) por
cada denominador y multiplicamos por su numerador, en ambos miembros.
2(x - 1) = x(x + 1) - (x2 - 1)
2x - 2 = x2 + x - x2 + 1
2x - 2 = + x + 1
2. Se hace la transposición de términos.
2x - x = 1 + 2
3. Se reducen los términos semejantes.
x = 3
Ejercicios de ecuaciones racionales de primer grado:
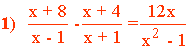
1. Se suprimen los denominadores. Se halla el m.c.m. de los denominadores de ambos miembros:
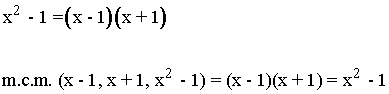
Dividimos el mínimo común multiplo (m.c.m.) por
cada denominador y multiplicamos por su numerador, en ambos miembros.
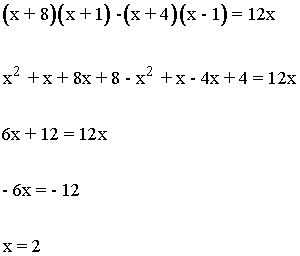
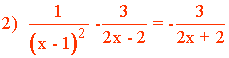
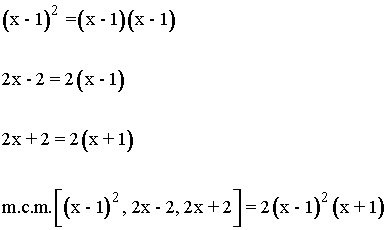
Dividimos el m.c.m. por cada denominador y multiplicamos por el numerador.
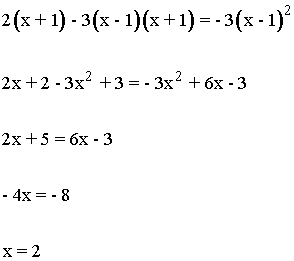
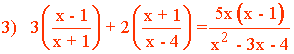
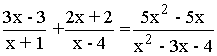
Para descomponer x2 - 3x - 4, resolvemos la ecuación de segundo grado.
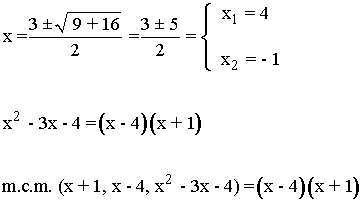
Dividimos el m.c.m. por cada denominador y multiplicamos por el numerador.
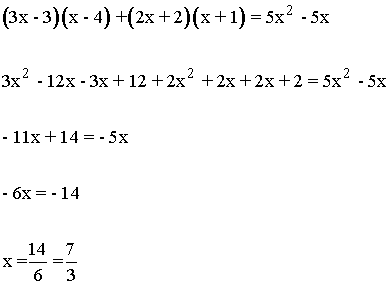
Ejercicios de ecuaciones racionales de primer grado:
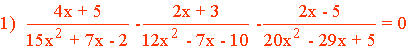
Para hallar el mínimo común multiplo factorizamos cada uno de los denominadores.
Resolvemos la ecuación de segundo grado 15x2 + 7x - 2.
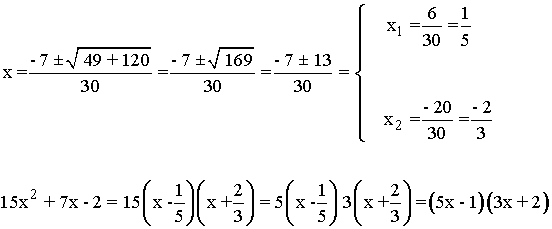
Resolvemos la ecuación de segundo grado 12x2 - 7x - 10.
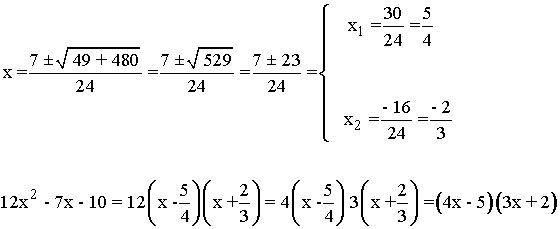
Resolvemos la ecuación de segundo grado 20x2 - 29x + 5.
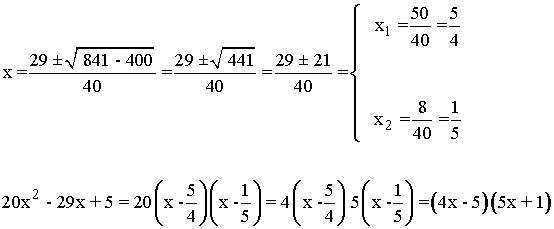
![]()
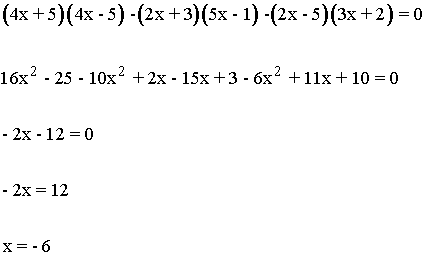
Ejercicio de una ecuación racional de primer grado:
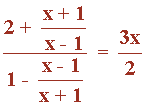
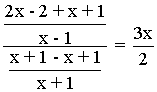
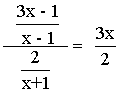
![]()
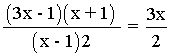
(3x - 1)(x + 1) = 3x(x - 1)
3x2 + 3x - x - 1 = 3x2 - 3x
5x = 1
x = 1/5
Ejercicio de una ecuación racional de primer grado:
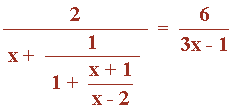
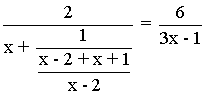
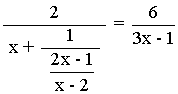
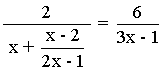
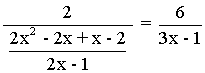
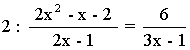
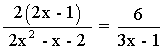
2(2x - 1)(3x - 1) = 6(2x2 - x - 2)
12x2 - 4x - 12x + 2 = 12x2 - 6x - 12
-4x - 12x + 6x = - 12 - 2
- 10x = - 14
x = 14/10 = 7/5
Ejercicio de una ecuación racional de primer grado:
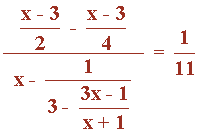
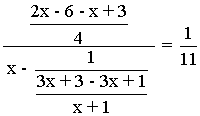
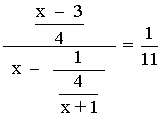
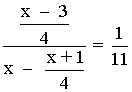
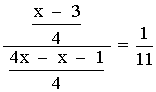
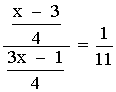
![]()
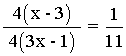
![]()
11(x - 3) = 3x - 1
11x - 33 = 3x - 1
11x - 3x = - 1 + 33
8x = 32
x = 4
Ejercicios de ecuaciones racionales de segundo grado:
![]()
m.c.m. (3, x) = 3x
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
3x2 + 3 = 10x
3x2 - 10x + 3 = 0
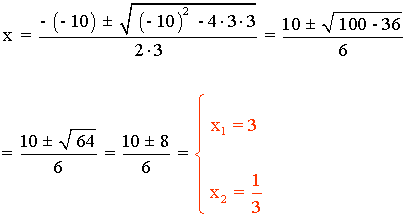
![]()
Aplicamos: m.c.m.(x, x - 120, 144) = 144x(x - 120)
144(x - 120) + 144x = x(x - 120) ⇔ 144x - 17280 + 144x = x2 - 120x ⇔ x2 - 408x + 17280 = 0
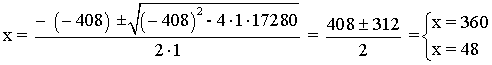
![]()
m.c.m. (x - 1, x + 2, x + 1) = (x - 1) (x + 2) (x + 1)
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
6(x + 2)(x + 1) - 10(x - 1)(x + 1) = 4(x - 1)(x + 2)
6x2 + 18x + 12 - 10x2 + 10 = 4x2 + 4x - 8
- 8x2 + 14x + 30 = 0
4x2 - 7x - 15 = 0
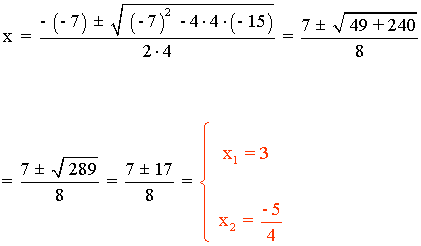
Ejercicios de ecuaciones racionales con literales:
A) Ecuaciones de primer grado:
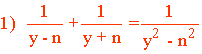
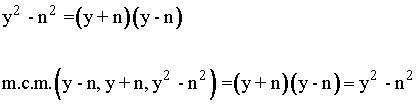
Dividimos el m.c.m. entre los denominadores y multiplicamos por su numerador en cada miembro.
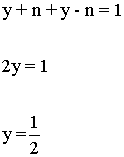
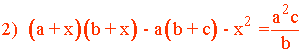
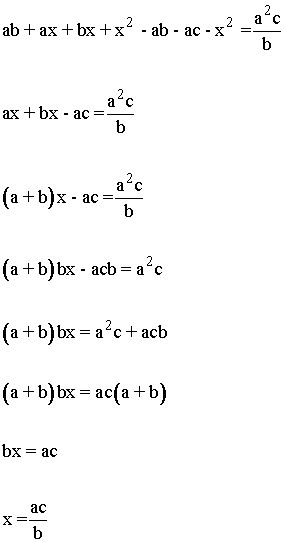
B) Ecuaciones de segundo grado:
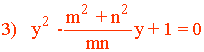
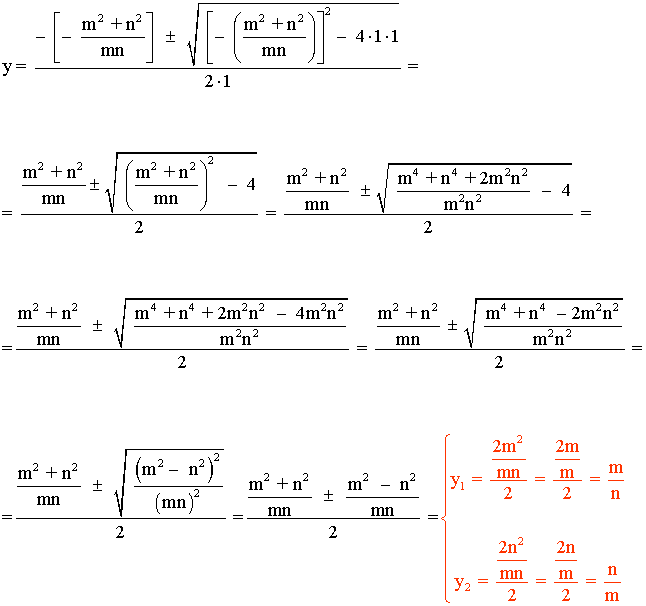
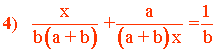
m.c.m. (b, a + b, x) = b (a+b) x
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
x2 + ab = (a + b)x
x2 - (a + b)x + ab = 0
Esta ecuación es la misma del apartado 2)
Es decir, x1 = a y x2 = b


 INICIO
INICIO