Razones trigonométricas de un ángulo cualquiera
Circunferencia goniométrica
Una circunferencia goniométrica es una circunferencia de radio 1 unidad de longitud y centrada en el origen de un sistema de coordenadas cartesianes.
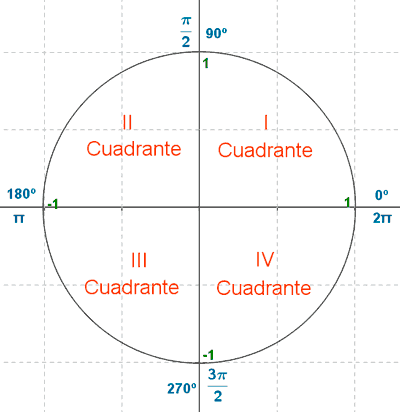
Razones trigonométricas de un ángulo cualquiera
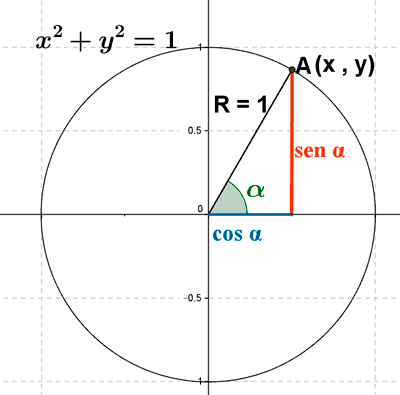
Al punto A le asignamos un ángulo:
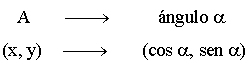
![]()
![]()
![]()
![]()
![]()
![]()
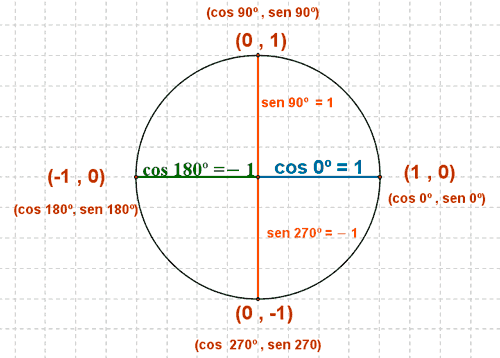
El seno de un ángulo α coincide con el valor de la ordenada en el punto: sen α = y
El coseno de un ángulo α coincide con el valor de la abscisa en el punto: cos α = x
La tangente de un ángulo α es el cociente entre la ordenada y la abscisa: tg α = y/x
Signo de las razones trigonométricas
En cada cuadrante el seno tiene el mismo signo que la ordenada y el coseno el mismo que la abscisa. El signo de la tangente se obtiene aplicando la regla de los signos de la división del seno entre el coseno.
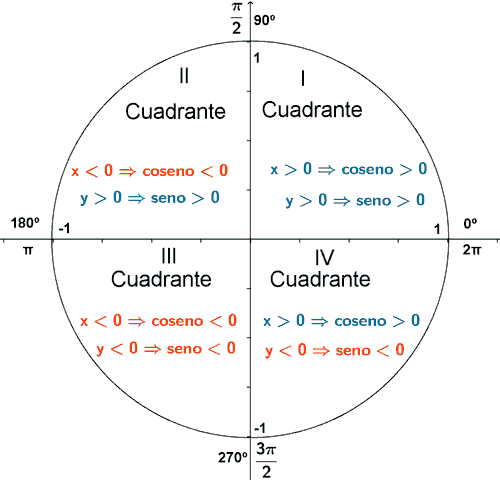
Seno, coseno y tangente de un ángulo entre 0o y 360o
Primer cuadrante
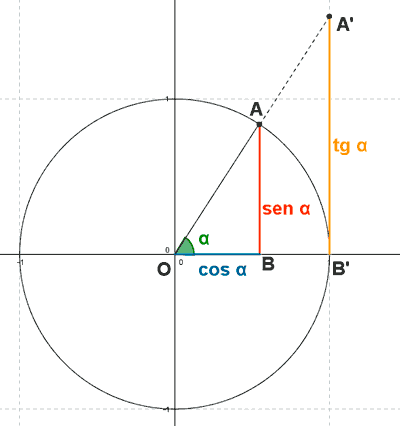
El punto A tiene coordenadas (x, y)
El punto A' tiene de coordenadas (1, y')
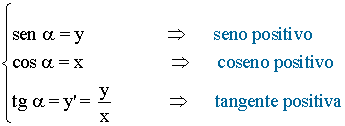
Segundo cuadrante
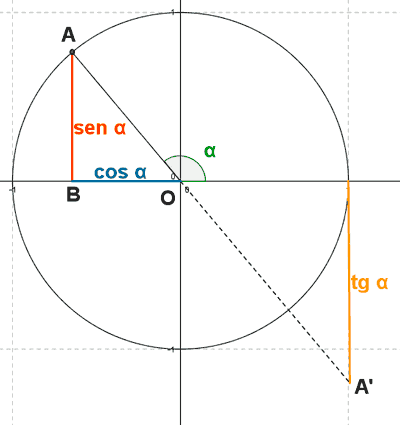
El punto A tiene coordenadas (-x, y)
El punto A' tiene de coordenadas (1, -y')
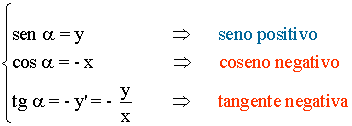
Tercer cuadrante
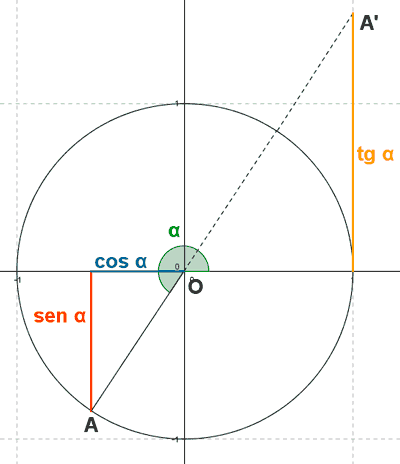
El punto A tiene coordenadas (-x, -y)
El punto A' tiene de coordenadas (1, y')
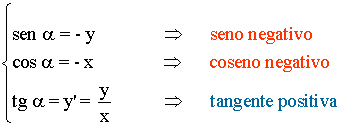
Cuarto cuadrante
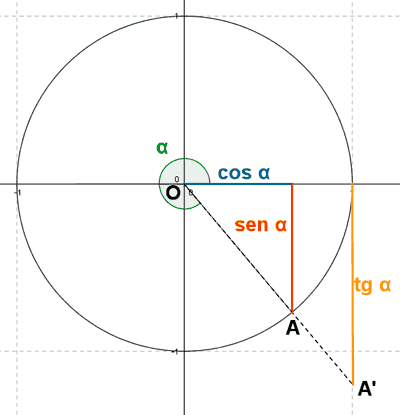
El punto A tiene coordenadas (x, -y)
El punto A' tiene de coordenadas (1, -y')
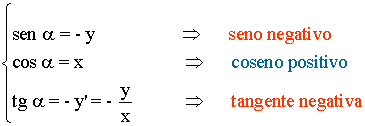
Razones trigonométricas de un ángulo en los cuadrantes
Al punto A le asignamos un ángulo:
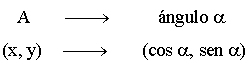
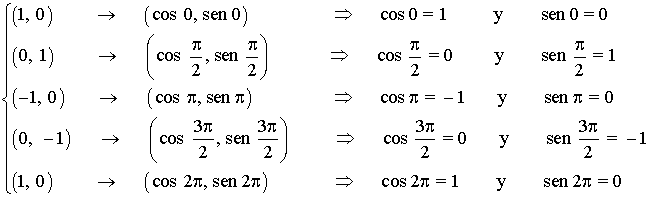
| 0 0º |
π/2 90º |
π 180º |
3π/2 270º |
2π 360º |
|
|---|---|---|---|---|---|
| seno | 0 |
1 |
0 |
- 1 |
0 |
| coseno | 1 |
0 |
- 1 |
0 |
1 |
| tangente | 0 |
No definida |
0 |
No definida |
0 |
Razones trigonométricas de un ángulo multiplo de 45º
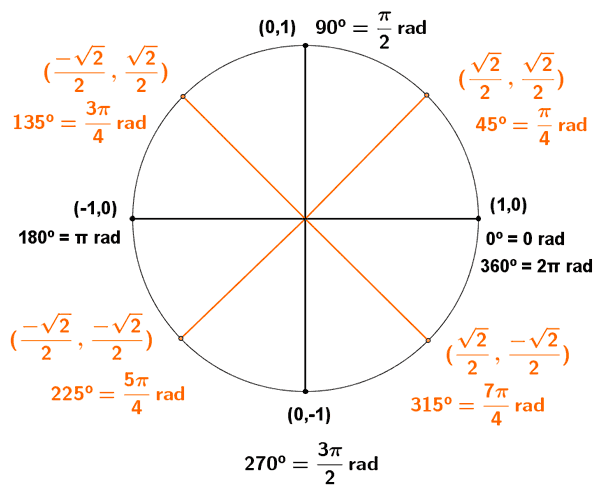
Razones trigonométricas de un ángulo multiplo de 30º y 60º
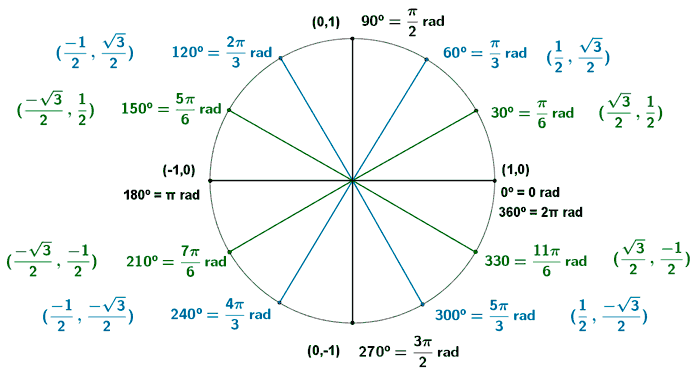
Ejemplos:
1) Demuestra que el punto P está en el círculo unitario o circunferencia goniométrica:
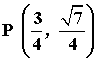
Para que se cumpla la ecuación del círculo unitario o circunferencia goniométrica, se tiene que dar que x2 + y2 = 1
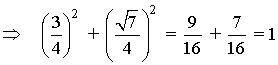
Es decir, el punto P está en el círculo unitario.
2) El punto P está en el tercer cuadrante. Encuentra su ordenada y para que dicho punto esté en el círculo unitario o circunferencia goniométrica:
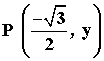
Para que se cumpla la ecuación del círculo unitario o circunferencia goniométrica, se tiene que dar que x2 + y2 = 1
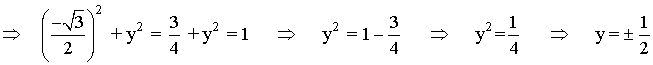
Como la coordenada y tiene que estar en el tercer cuadrante, descartamos la solución positiva:
![]()
3) Calcula el punto sobre la circunferencia del círculo unitario o circunferencia goniométrica determinado por los siguientes ángulos:
![]()
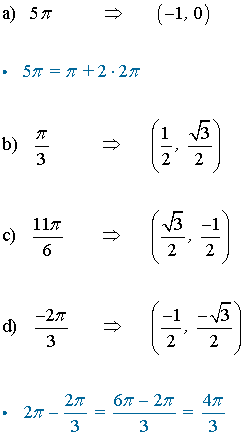


 INICIO
INICIO

