INICIOResumen de razones trigonométricas
Medida de ángulos
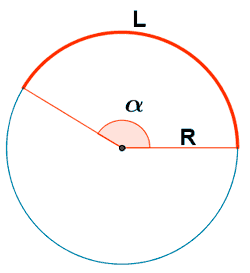
π radianes = 180º
(α en radianes)
Definición de las funciones trigonométricas
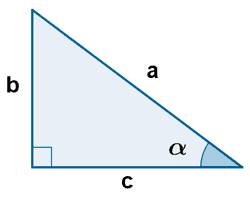
| a = hipotenusa | b = cateto opuesto | c = cateto contiguo |
|---|---|---|
 |
 |
 |
 |
 |
 |
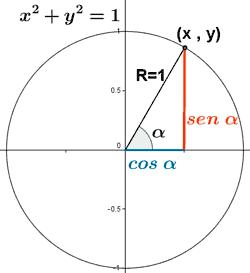
| R = 1 (hipotenusa) | y = cateto opuesto | x = cateto contiguo |
|---|---|---|
 |
 |
 |
 |
 |
 |
Funciones trigonométricas de los ángulos notables
| 0 0º |
π/6 30º |
π/4 45º |
π/3 60º |
π/2 90º |
π 180º |
3π/2 270º |
2π 360º |
|
|---|---|---|---|---|---|---|---|---|
| seno | 0 |
 |
 |
 |
1 |
0 |
- 1 |
0 |
| coseno | 1 |
|
|
|
0 |
- 1 |
0 |
1 |
| tangente | 0 |
 |
1 |
 |
No definida |
0 |
No definida |
0 |
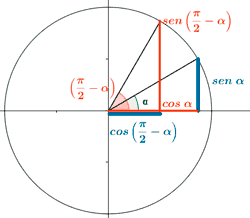
Ángulos complementarios (su suma vale π/2 radianes)
Ángulos que difieren en π/2
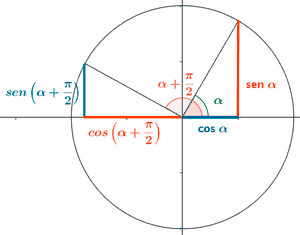
Ángulos suplementarios (su suma vale π radianes)
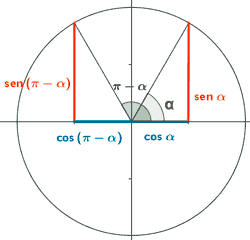
sen(π - α) = sen α
cos(π - α) = - cos α
tg(π - α) = - tg α
Ángulos que se diferencian en π radianes
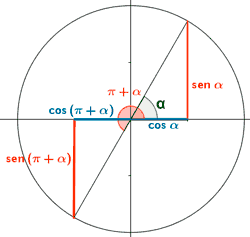
sen (π + α) = - sen α
cos (π + α) = - cos α
tg (π + α) = tg α
Ángulos opuestos
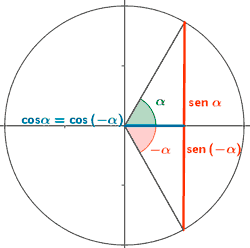
sen (-α) = - sen α
cos (-α) = cos α
tg (-α) = - tg α
