Reducción de razones trigonométricas al primer cuadrante

Ángulos complementarios.
Ángulos que suman 90^o: α y 90^o- α

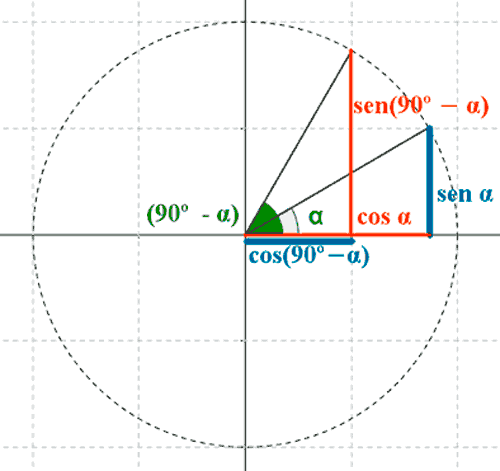
ángulos complementarios

Dos ángulos son complementarios si suman 90^o

α + β = 90^o ⇒ β = 90^o - α

sen (90^o- α) = cos α

cos (90^o - α) = sen α

tg (90^o - α) = cotg α

Dos ángulos son suplementarios si suman π/2 radianes

α + β = π/2 rad ⇒ β = π/2 - α

Hallar las razones trigonométricas de 60^o

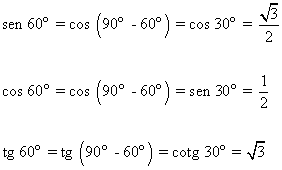
Paso del segundo cuadrante al primero.
Ángulos suplementarios: α y 180^o - α

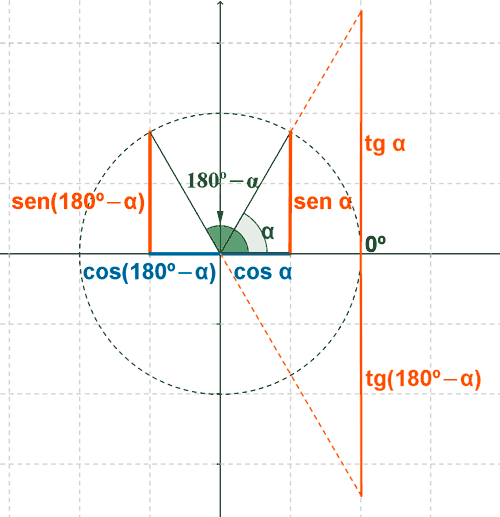
ángulos suplementarios

Dos ángulos son suplementarios si suman 180^o

α + β = 180^o ⇒ β = 180^o - α

sen (180^o- α) = sen α

cos (180^o - α) = - cos α

tg (180^o - α) = - tg α

Dos ángulos son suplementarios si suman π radianes

α + β = π rad ⇒ β = π - α

sen (π - α) = sen α

cos (π - α) = - cos α

tg (π - α) = - tg α

Hallar las razones trigonométricas de 150^o

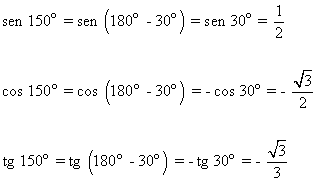
Paso del tercer cuadrante al primero.
Ángulos que difieren en 180^o: α y α + 180^o

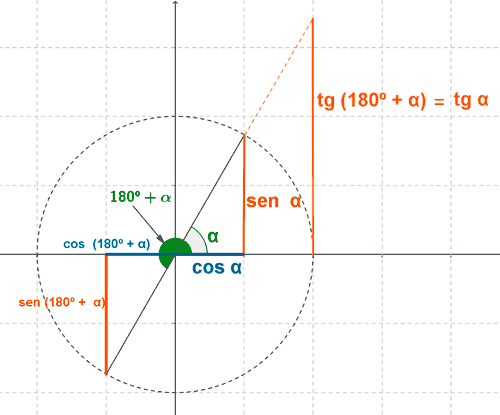
ángulos que difieren en 180º

sen (180^o + α) = - sen α

cos (180^o + α) = - cos α

tg (180^o + α) = tg α

sen (π + α) = - sen α

cos (π + α) = - cos α

tg (π + α) = tg α

Hallar las razones trigonométricas de 225^o

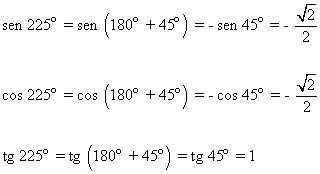
Paso del cuarto cuadrante al primero.
Ángulos que suman 360^o

angulos que suman 360º

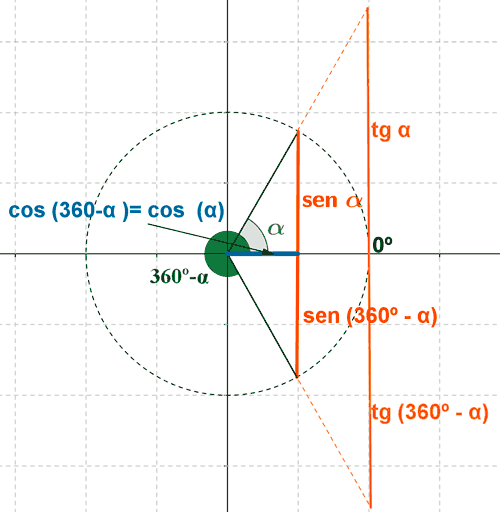
Ángulos que suman un ángulo completo

a + ß = 360^o ? ß = 360^o - a

sen (360^o - α) = - sen α

cos (360^o - α) = cos α

tg (360^o - α) = - tg α

Ángulos que suman un ángulo completo

a + ß = 2π rad ? ß = 2π - a

sen (2π - α) = - sen α

cos (2π - α) = cos α

tg (2π - α) = - tg α

Hallar las razones trigonométricas de 300^o

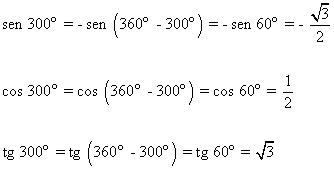
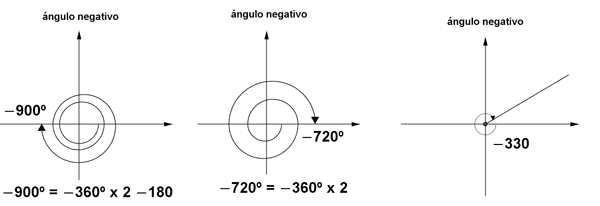
Ángulos opuestos o ángulos negativos

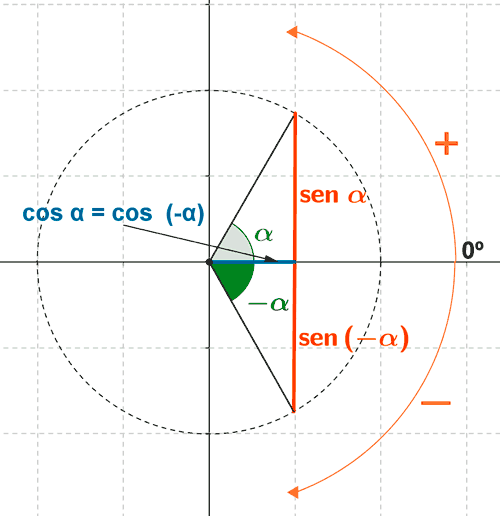
ángulos opuestos

sen (-α) = - sen α

cos (-α) = cos α

tg (-α) = - tg α

sen (-α) = sen (360^o - α) = - sen α

cos (-α) = cos (360^o - α) = cos α

tg (-α) = tg (360^o - α) = - tg α

Reducción de un ángulo al primer giro:
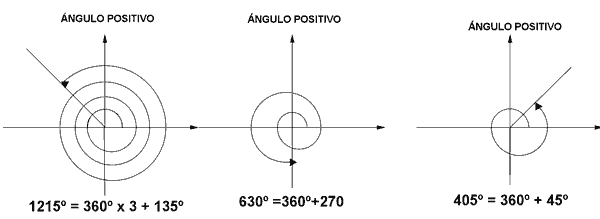
Ángulos mayores de 360^o

Dos ángulos α y k·360^o+α que difieren en un número entero de vueltas, son equivalentes:

y sus razones trigonométricas coinciden.

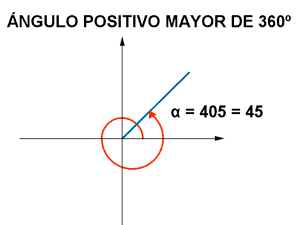
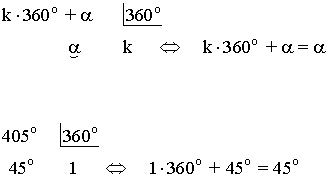
Halla las razones trigonométricas de 1320^o

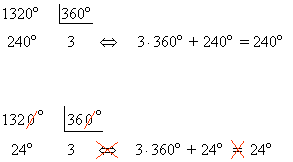
En la división de ángulos no podemos tachar ceros comunes al dividendo y al divisor ya que aunque obtendríamos el mismo cociente, el resto sería diferente.

El ángulo resultante es del tercer cuadrante, por tanto lo podemos reducir al primer cuadrante por ángulos que difieren en 180^o:

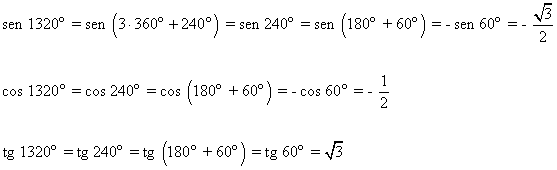
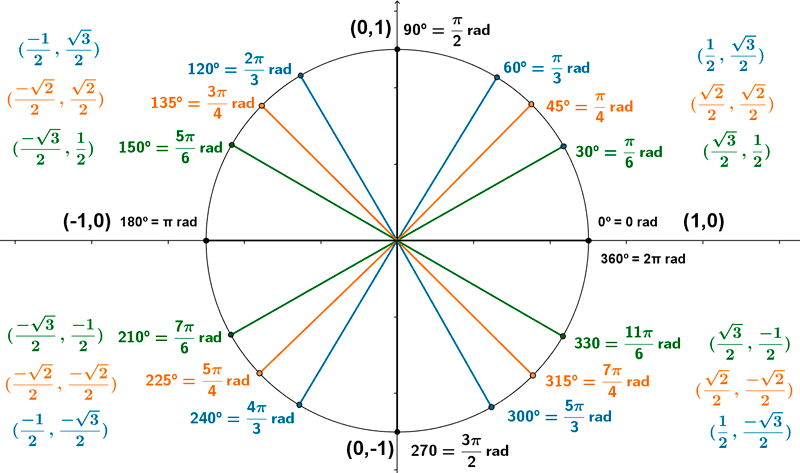
Resumen de los ángulos notables: circunferencia unitaria de 16 puntos

circunferencia unitaria 16 puntos