Resolución de triángulos cualesquiera
Para resolver un triángulo cualquiera utilizamos las siguientes relaciones:
• Los tres ángulos de un triángulo suman 180o
• Teorema del seno
• Teorema del coseno
Caso I: Se conocen dos ángulos y un lado
Se aplican las siguientes fórmulas:
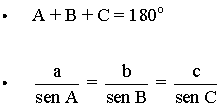
• Solución única.
Ejemplo
Resuelve un triángulo en el que se conocen: a = 4,5 m y los ángulos B = 37o y C = 61o
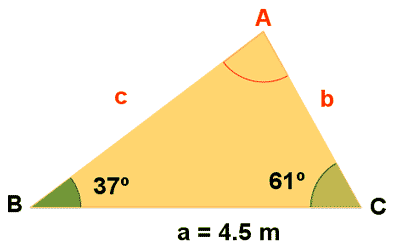
| Datos | Incógnitas | Fórmulas | Resultado |
|---|---|---|---|
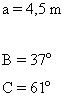 |
A |
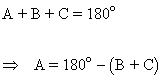 |
|
b |
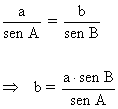 |
||
c |
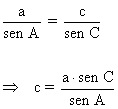 |
||
Área |
Caso II: Se conocen dos lados y el ángulo comprendido entre ellos
• Se aplican los teoremas del coseno y del seno.
• Tiene solución única.
Ejemplo
Resuelve un triángulo en el que se conocen: a = 8,7 m y b = 5,4 m y el ángulo C = 63o
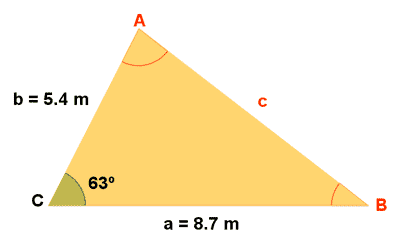
| Datos | Incógnitas | Fórmulas | Resultado |
|---|---|---|---|
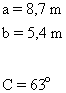 |
c |
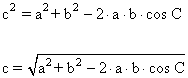 |
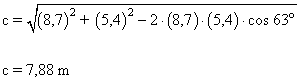 |
A |
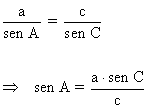 |
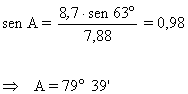 |
|
B |
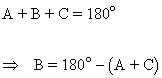 |
||
Área |
Caso III: Se conocen dos lados y el ángulo opuesto a uno de ellos
• Para resolverlo se comienza aplicando el teorema del seno.
• Tiene dos soluciones, una o ninguna.
Ejemplo con una única solución
A) Resuelve un triángulo en el que se conocen: a = 7,5 m y b = 8 m y el ángulo B = 50o
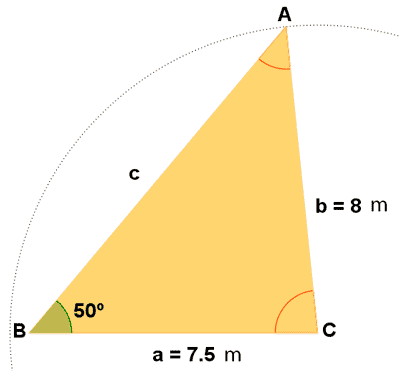
| Datos | Incógnitas | Fórmulas | Resultado |
|---|---|---|---|
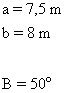 |
A |
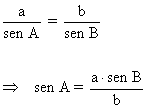 |
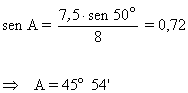 |
C |
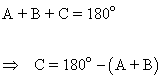 |
||
c |
 |
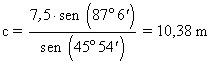 |
|
Área |
Ejemplo con dos soluciones
B) Resuelve un triángulo en el que se conocen: a = 7,5 m y b = 6,2 m y el ángulo B = 50o
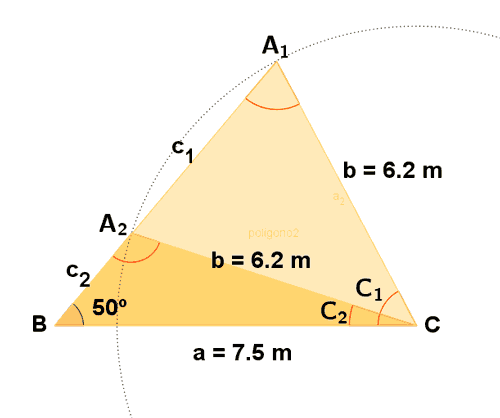
Los triángulos definidos son:
![]()
Y el lado c es:
![]()
| Datos | Incógnitas | Fórmulas | Resultado |
|---|---|---|---|
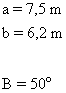 |
A |
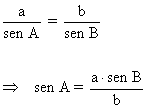 |
 |
C |
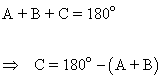 |
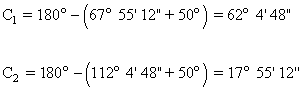 |
|
c |
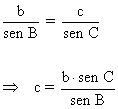 |
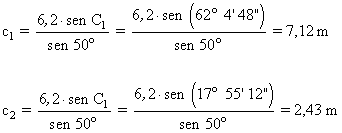 |
|
Área |
 |

Ejemplo sin solución
C) Resuelve un triángulo en el que se conocen: a = 7,5 m y b = 5 m y el ángulo B = 50o
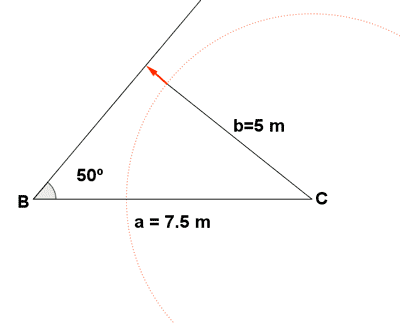
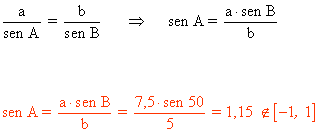
El seno de un ángulo no puede ser mayor que 1.
Por lo tanto, no existe solución, pues corresponde a la situación de la figura, donde el lado b es demasiado corto para cerrar el triángulo.
Caso IV: Se conocen los tres lados
• La solución se consigue aplicando el teorema del coseno.
• Tiene una o ninguna solución.
Ejemplo con una única solución
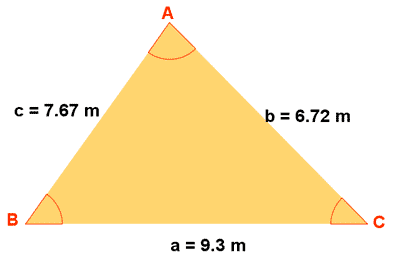
A) Resuelve un triángulo en el que se conocen: a = 9,3 m , b = 6,72 m y c = 7,67 m
| Datos | Incógnitas | Fórmulas | Resultado |
|---|---|---|---|
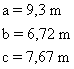 |
A |
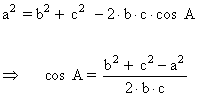 |
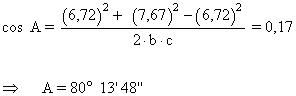 |
B |
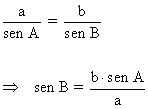 |
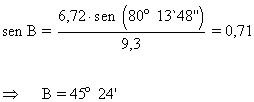 |
|
C |
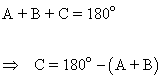 |
||
Área |
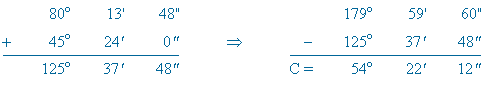
Ejemplo sin solución
B) Resuelve un triángulo en el que se conocen: a = 5 m , b = 7 m y c = 15 m
Al ser c > a + b no se puede construir el triángulo, por lo que no existe solución


 INICIO
INICIO
