Volumen del prisma y del cilindro.
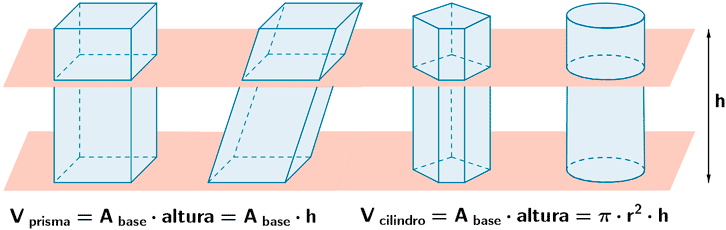
Las secciones son siempre iguales al A base por tanto podemos afirmar que las secciones por un plano paralelo a sus bases tienen el mismo área.
Por el principio de Cavalieri, los cuatro cuerpos tienen el mismo volumen, que podemos calcular a partir del volumen del ortoedro.
V ortoedro = V prisma oblicuo = V prisma recto = V cilindro
Volumen del prisma.
El volumen de un prisma de altura h y área de la base A base , es :
V prisma = A base · h
volumen del cilindro.
El volumen de un cilindro de altura h y radio de la base r es :
V cilindro = π · r 2 · h
Ejemplo 1 :
Halla los volúmenes de los siguientes cuerpos geométricos :
a) Un prisma recto de altura 110 cm y base un cuadrado de lado 25 cm. ¿Obtendrías el mismo resultado si el prisma fuera oblicuo?
b) Un cilindro de radio 10 cm y altura 95 cm.
a)
El volumen del prisma viene determinado por la siguiente expresión :
V prisma = A base · h = 25 · 25 · 110 = 68750 cm 3
Si el prisma fuera oblicuo, según el principio de Cavalieri, el volumen sería el mismo ya que tienen la misma altura.
b)
Aplicamos la fórmula para calcular el volumen del cilindro :
V cilindro = π · r 2 · h = 3,14 · 10 2 · 95 = 29830 cm 3


 INICIO
INICIO

