Problemas resueltos de volumen III
1) Halla el volumen de un prisma cuadrangular, de lado de la base 5 cm y altura 12 cm. Calcula también el volumen del cilindro inscrito en el prisma.
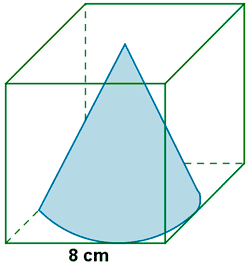
2) Halla el volumen entre el cono y el cubo :
3) Determina el volumen de las esferas circunscrita e inscrita en un cilindro de altura y diámetro 1 m. ¿Cuál es la diferencia entre los radios de ambas esferas?
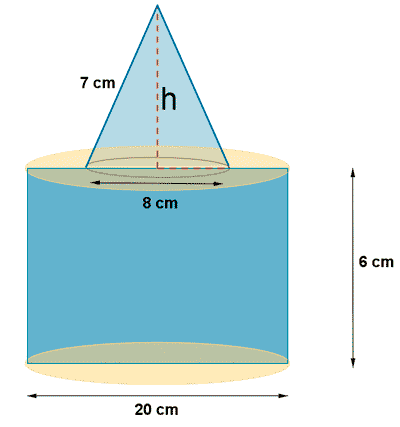
4) Calcular el volumen de la siguiente figura.
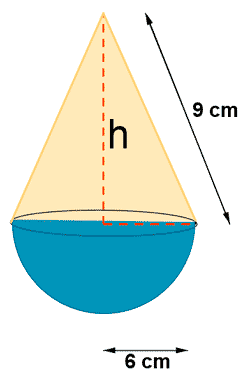
5) Calcular el volumen de la siguiente cuerpo.
Ejercicios de áreas y volúmenes I
Ejercicios de áreas y volúmenes II
1) Halla el volumen de un prisma cuadrangular, de lado de la base 5 cm y altura 12 cm. Calcula también el volumen del cilindro inscrito en el prisma.
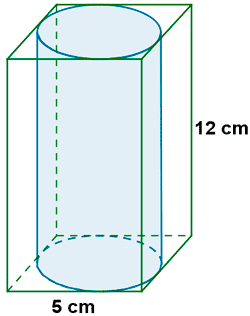
V prisma = A base · h → V prisma = 5 2 · 12 = 300 cm 3
El cilindro inscrito tiene por radio de su base la mitad del lado del cuadrado, es decir, 2,5 centímetros.
V cilindro = A base · h → V cilindro = π · r 2 · h → V cilindro = 3,14 · 2,5 2 · 12 = 235,5 cm 3
2) Halla el volumen entre el cono y el cubo :

Para calcular el volumen que nos piden, calculamos en primer lugar el volumen del cubo. Una vez tenemos el volumen del cubo, le restamos el volumen del cono. De esta forma, resulta el volumen pedido.
V cubo = a 3 = 8 3 = 512 cm 3
![]()
V comprendido = V cubo - V cono = 512 - 133,97 = 378,03 cm 3
3) Determina el volumen de las esferas circunscrita e inscrita en un cilindro de altura y diámetro 1 m. ¿Cuál es la diferencia entre los radios de ambas esferas?

El radio de la esfera inscrita mide la mitad del diámetro del cilindro, por lo ue su radio es 0,5 m. Su volumen es :
![]()
El radio de la esfera circunscrita podemos obtenerlo de la figura siguiente, para poder así calcular su volumen :


) Calcular el volumen de la siguiente figura.

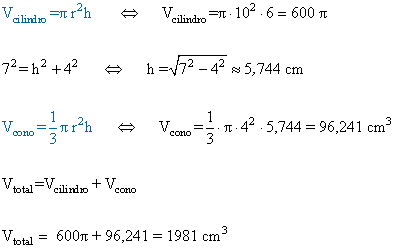
5) Calcular el volumen de la siguiente cuerpo.

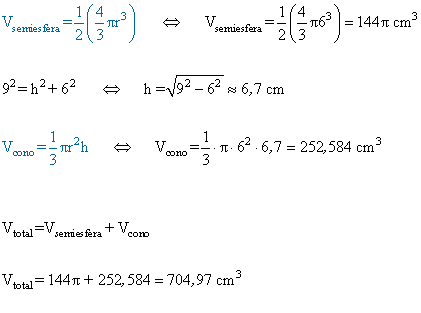


 INICIO
INICIO