Parámetros estadísticos III : medidas de posición.
Cuartiles.
Los cuartiles Q 1 , Q 2 y Q 3 son tres valores de la variable estadística que divide en cuatro partes el número de datos. Es decir, que cada tramo será el 25% de los datos recogidos en el estudio.
El cuartil Q 2 coincide con la mediana.
Diagrama de caja.
Es una representación de distribuciones estadísticas en la que el 50% de los valores centrales se destacan mediante un rectánculo ( caja ) y los valores extremos, el 25% de los menores y el 25% de los mayores, se representan mediante segmentos llamados bigotes.
Los puntos que separan los cuatro trozos son los cuartiles y la mediana.
Ejemplo 1 :
La tabla muestra las temperaturas en Londres a lo largo de cien días. Halla los cuartiles y el diagrama de caja asociado.
| Temperatura | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|
| Nº de días | 10 | 17 | 40 | 22 | 5 | 6 |
Para calcular los cuartiles vamos a necesitar las frecuencias absolutas acumuladas.
| Temperatura x i |
Nº de días f i |
F i |
|---|---|---|
| 15 | 10 | 10 |
| 16 | 17 | 27 |
| 17 | 40 | 67 |
| 18 | 22 | 89 |
| 19 | 5 | 94 |
| 20 | 6 | 100 |
Para obtener el valor del primer cuartil, dividiremos la población entre 4 ( 25 % de datos), y elegiremos la primera x i cuya frecuencia absoluta sea mayor.
Para el tercer cuartil procedremos igual pero multiplicando por 3 y dividiendo por 4 ( 75 % de los datos ).
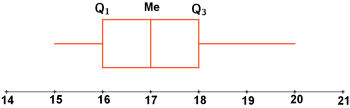
Para obtener el diagrama de caja será necesario también calcular la mediana.
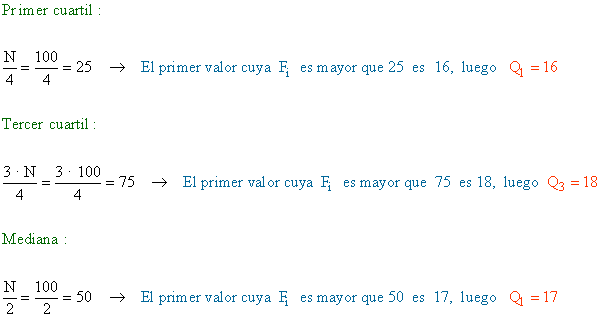
Ejemplo 2 :
Calcula los cuartiles y mediana de los siguientes datos para representarlos en un diagrama de caja.
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| fi | 2 | 4 | 9 | 11 | 3 | 1 | 8 | 5 | 7 |
| Fi | 2 | 6 | 15 | 26 | 29 | 30 | 38 | 43 | 50 |

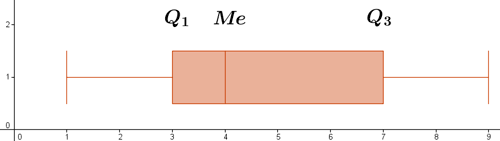
Representamos ahora estos datos en un diagrama de caja, trazando una recta y dibujando un rectángulo de anchura comprendida entre Q1 y Q3.


 INICIO
INICIO
