Ejercicios resueltos de estadística.
1) Las notas de matemáticas de los alumnos de una clase son las siguientes:
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias.
2) Completa la siguiente tabla de frecuencias con las frecuencias acumuladas.
| x i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| f i | 6 | 15 | 10 | 12 | 7 |
3) Las notas de matemáticas de los alumnos de una clase son las siguientes :
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias, la media aritmética, la mediana y la moda.
4)
Un especialista en pediatría obtuvo la siguiente tabala sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez :
| Meses | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|
| Niños | 1 | 4 | 9 | 16 | 11 | 8 | 1 |
Dibujar el polígono de frecuencias. Calcular la mediana y la moda.
5) Un médico atendió en 200 días las siguientes urgencias:
1, 3, 1, 1, 0, 1, 0, 2, 2, 0, 0, 1, 1, 2, 0, 6, 3, 1, 4, 0
a) Resumir los datos en una tabla que muestre frecuencias absolutas y porcentajes, y dibujar el correspondiente diagrama de barras.
b) Calcular la media, la mediana y la moda del conjunto de datos. ¿Es simétrica la distribución anterior?
6) Dadas las notas de un test con una puntuación del 0 al 6 de 128 alumnos,
representar, mediante un diagrama de caja, la siguiente distribución, previo cálculo de la mediana y cuartiles :
| x i | f i | F i |
|---|---|---|
| 0 | 15 | 15 |
| 1 | 20 | 35 |
| 2 | 44 | 79 |
| 3 | 27 | 106 |
| 4 | 13 | 119 |
| 5 | 7 | 126 |
| 6 | 2 | 128 |
7) De los siguientes datos calcula : mediana, cuartil primero, cuartil tercero y el diagrama de caja.
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| fi | 2 | 4 | 9 | 11 | 3 | 1 | 8 | 5 | 7 |
| Fi | 2 | 6 | 15 | 26 | 29 | 30 | 38 | 43 | 50 |
8) Completar los datos que faltan en la siguiente tabla estadística, donde hi, Fi y fi, representan, respectivamente, la frecuencia relativa, absoluta acumulada y absoluta.
Calcular además: media, moda y mediana de la distribución.
| x i | f i | F i | h i |
|---|---|---|---|
| 1 | 4 | 0,08 | |
| 2 | 4 | ||
| 3 | 16 | 0,16 | |
| 4 | 7 | 0,14 | |
| 5 | 5 | 28 | |
| 6 | 38 | ||
| 7 | 7 | 45 | |
| 8 |
9) Hallar la desviación media de las siguientes distribuciones :
a) 6, 7, 8, 10, 11, 12, 14, 15, 16, 17
b) 5, 5, 5, 6, 7, 7, 8, 8, 9, 10
10) Calcula la desviación media de los siguientes datos :
| x i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f i | 6 | 7 | 10 | 3 | 5 | 9 |
11) El siguiente pictograma refleja el mes de nacimiento de los alumnos de ESO de un colegio.
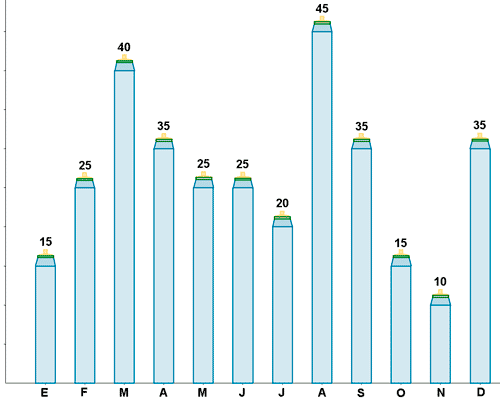
a) Construye la tabla de frecuencias correspondiente.
b) Indica cúal es el valor de la moda y calcula la media mensual de nacimientos.
1) Las notas de matemáticas de los alumnos de una clase son las siguientes:
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias.
| Nota xi |
Frecuencia absoluta fi |
Frecuencia relativa hi |
Frecuencia absoluta acumulada Fi |
Frecuencia relativa acumulada Hi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1/30 = 0,033 | 1 | 0,033 |
| 3 | 3 | 3/30 = 0,1 | 1 + 3 = 4 | 0,033 + 0,1 = 0,133 |
| 4 | 4 | 4/30 = 0,133 | 4 + 4 = 8 | 0,133 + 0,133 = 0,266 |
| 5 | 6 | 6/30 = 0,2 | 8 + 6 = 14 | 0,266 + 0,2 = 0,466 |
| 6 | 7 | 7/30 = 0,234 | 14 + 7 = 21 | 0,466 + 0,234 = 0,7 |
| 7 | 5 | 5/30 = 0,167 | 21 + 5 = 26 | 0,7 + 0,167 = 0,867 |
| 8 | 2 | 2/30 = 0,067 | 26 + 2 = 28 | 0,867 + 0,067 = 0,934 |
| 9 | 1 | 1/30 = 0,033 | 28 + 1 = 29 | 0,934 + 0,33 = 0,967 |
| 10 | 1 | 1/30 = 0,033 | 29 + 1 = 30 | 0,967 + 0,033 = 1 |
2) Completa la siguiente tabla de frecuencias con las frecuencias acumuladas.
| x i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| f i | 6 | 15 | 10 | 12 | 7 |
Escribimos la tabla con las columnas de frecuencias absolutas, frecuencias relativas y frecuencias absolutas y relativas acumuladas.
| Variable estadística x i |
Frecuencia absoluta f i |
Frecuencia relativa h i |
Frecuencia absoluta acumulada F i |
Frecuencia relativa acumulada H i |
|---|---|---|---|---|
| 1 | 6 | 6 | 0,12 | |
| 2 | 15 | 15 + 6 = 21 | 0,12 + 0,3 = 0,42 | |
| 3 | 10 | 10 + 21 = 31 | 0,2 + 0,42 = 0,62 | |
| 4 | 12 | 12 + 31 = 33 | 0,24 + 0,62 = 0,86 | |
| 5 | 7 | 33 + 7 = 50 | 0,14 + 0,86 = 1 |
La última frecuencia absoluta acumulada coincide con el número total de datos.
La última frecuencia relativa acumulada es siempre 1.
3) Las notas de matemáticas de los alumnos de una clase son las siguientes :
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias, la media aritmética, la mediana y la moda.
| Variable estadística xi |
Frecuencia absoluta fi |
Frecuencia relativa hi |
Frecuencia absoluta acumulada Fi |
Frecuencia relativa acumulada Hi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0,033 | 1 | 0,033 |
| 3 | 3 | 0,1 | 4 | 0,133 |
| 4 | 4 | 0,133 | 8 | 0,266 |
| 5 | 6 | 0,2 | 14 | 0,466 |
| 6 | 7 | 0,234 | 21 | 0,7 |
| 7 | 5 | 0,167 | 26 | 0,867 |
| 8 | 2 | 0,067 | 28 | 0,934 |
| 9 | 1 | 0,033 | 29 | 0,967 |
| 10 | 1 | 0,033 | 30 | 1 |
| Sumatorio | N = 30 | 1 |
Media aritmética :
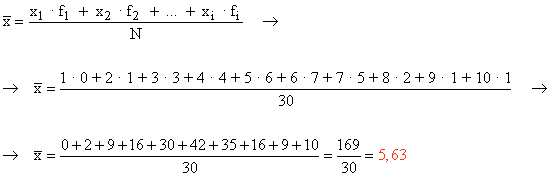
Moda :
La moda es el valor estadístico que más se repite, es decir, con l mayor frecuencia estadística. Luego la moda es : Mo = 6
Mediana :
![]() → El primer valor estadístico vuya frecuencia absoluta acumulada es mayor a 15 es 6, por lo que la mediana es : Me = 6
→ El primer valor estadístico vuya frecuencia absoluta acumulada es mayor a 15 es 6, por lo que la mediana es : Me = 6
4)
Un especialista en pediatría obtuvo la siguiente tabala sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez :
| Meses | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|
| Niños | 1 | 4 | 9 | 16 | 11 | 8 | 1 |
Dibujar el polígono de frecuencias. Calcular la mediana y la moda.
Dibujamos en primer lugar el polígono de frecuencias. Este se obtiene mediante segmentos, uniendo los puntos siguientes : ( 9, 1 ), ( 10, 4 ), ( 11, 9 ), ( 12, 16 ), ( 13, 11 ), ( 14, 8 ) y ( 15, 1 ).
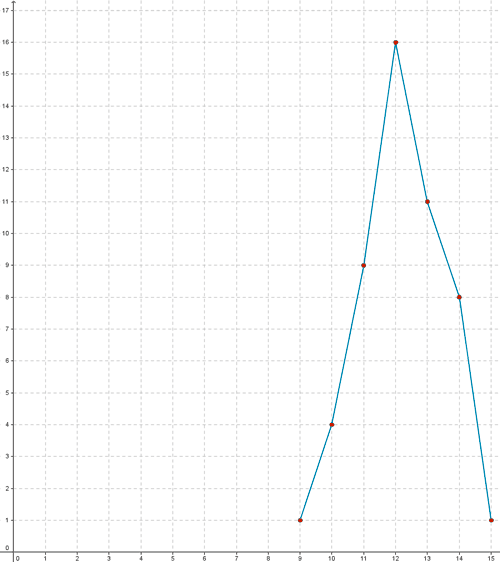
| xi | ni | Ni |
|---|---|---|
| 9 | 1 | 1 |
| 10 | 4 | 5 |
| 11 | 9 | 14 |
| 12 | 16 | 30 |
| 13 | 11 | 41 |
| 14 | 8 | 49 |
| 15 | 1 | 50 |
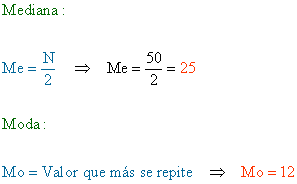
5) Un médico atendió en 200 días las siguientes urgencias:
1, 3, 1, 1, 0, 1, 0, 2, 2, 0, 0, 1, 1, 2, 0, 6, 3, 1, 4, 0
a) Resumir los datos en una tabla que muestre frecuencias absolutas y dibujar el correspondiente diagrama de barras.
b) Calcular la media, la mediana y la moda del conjunto de datos.
a)
| xi | f i | h i |
|---|---|---|
| 0 | 6 | 0,30 |
| 1 | 7 | 0,35 |
| 2 | 3 | 0,15 |
| 3 | 2 | 0,10 |
| 4 | 1 | 0,05 |
| 6 | 1 | 0,05 |
| Sumatorio: | 20 | 1 |
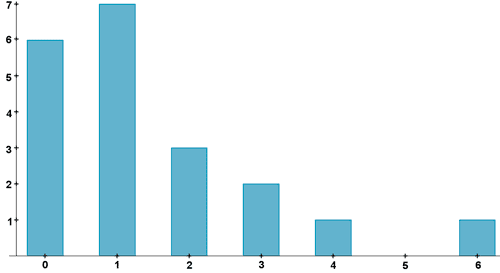
b)
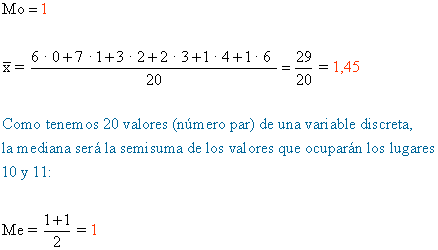
6) Dadas las notas de un test con una puntuación del 0 al 6 de 128 alumnos,
representar, mediante un diagrama de caja, la siguiente distribución, previo cálculo de la mediana y cuartiles :
| x i | f i | F i |
|---|---|---|
| 0 | 15 | 15 |
| 1 | 20 | 35 |
| 2 | 44 | 79 |
| 3 | 27 | 106 |
| 4 | 13 | 119 |
| 5 | 7 | 126 |
| 6 | 2 | 128 |
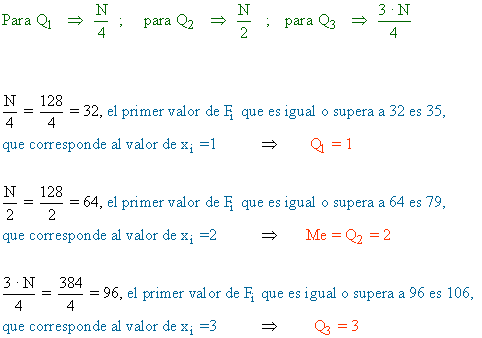
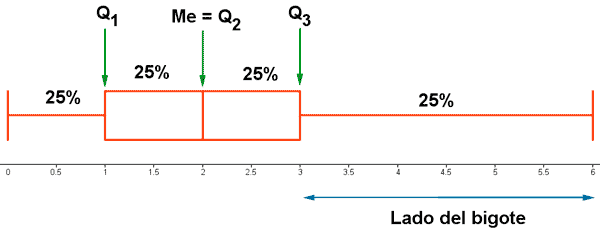
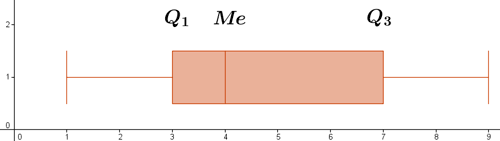
7) De los siguientes datos calcula : mediana, cuartil primero, cuartil tercero y el diagrama de caja.
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| fi | 2 | 4 | 9 | 11 | 3 | 1 | 8 | 5 | 7 |
| Fi | 2 | 6 | 15 | 26 | 29 | 30 | 38 | 43 | 50 |
En primer lugar vamos a calcular la mediana y los cuartiles primero y tercero.

Representamos ahora estos datos en un diagrama de caja, trazando una recta y dibujando un rectángulo de anchura comprendida entre Q1 y Q3.
8) Completar los datos que faltan en la siguiente tabla estadística, donde hi, Fi y fi, representan, respectivamente, la frecuencia relativa, absoluta acumulada y absoluta.
Calcular además: media, moda y mediana de la distribución.
| x i | f i | F i | h i |
|---|---|---|---|
| 1 | 4 | 0,08 | |
| 2 | 4 | ||
| 3 | 16 | 0,16 | |
| 4 | 7 | 0,14 | |
| 5 | 5 | 28 | |
| 6 | 38 | ||
| 7 | 7 | 45 | |
| 8 |

| x i | f i | F i | h i |
|---|---|---|---|
| 1 | 4 | 4 | 0,08 |
| 2 | 4 | 8 | 0,08 |
| 3 | 8 | 16 | 0,16 |
| 4 | 7 | 23 | 0,14 |
| 5 | 5 | 28 | 0,1 |
| 6 | 10 | 38 | 0,2 |
| 7 | 7 | 45 | 0,14 |
| 8 | 5 | 50 | 0,1 |

9) Hallar la desviación media de las siguientes distribuciones :
a) 6, 7, 8, 10, 11, 12, 14, 15, 16, 17
b) 5, 5, 5, 6, 7, 7, 8, 8, 9, 10
a)
Media de la distribución :
![]()
| x i | 6 | 7 | 8 | 10 | 11 | 12 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distancia a la media | 5,6 | 4,6 | 3,6 | 1,6 | 0,6 | 1,6 | 3,6 | 4,6 | 5,6 | 6,6 |
Desviación media :
![]()
b)
Media de la distribución :
![]()
| x i | 5 | 5 | 5 | 6 | 7 | 7 | 8 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distancia a la media | 2 | 2 | 2 | 1 | 0 | 0 | 1 | 1 | 2 | 3 |
Desviación media :
![]()
10) Calcula la desviación media de los siguientes datos :
| x i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f i | 6 | 7 | 10 | 3 | 5 | 9 |
| Variable estadística x i |
Frecuencia absoluta f i |
f i · x i | ||
|---|---|---|---|---|
| 1 | 6 | 6 | 3,525 - 1 = 2,525 | 15,15 |
| 2 | 7 | 14 | 3,525 - 2 = 1,525 | 10,675 |
| 3 | 10 | 30 | 3,525 - 3 = 0,525 | 5,25 |
| 4 | 3 | 12 | 4 - 3,525 = 0,475 | 1,425 |
| 5 | 5 | 25 | 5 - 3,525 = 1,475 | 7,375 |
| 6 | 9 | 54 | 6 - 3,525 = 2,475 | 22,275 |
| Total | 40 | 141 | 62,15 |
Media aritmética :
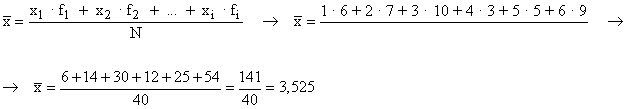
Desviación media :
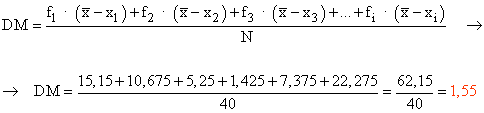
Podríamos decir que las variables estadísticas se encuentran alejadas de la media en 1,55 unidades de promedio.
11) El siguiente pictograma refleja el mes de nacimiento de los alumnos de ESO de un colegio.

a) Construye la tabla de frecuencias correspondiente.
b) Indica cúal es el valor de la moda y calcula la media mensual de nacimientos.
| x i | f i | h i | F i | H i |
|---|---|---|---|---|
| Enero | 15 | 15/325 = 0,046 | 15 | 0,046 |
| Febrero | 25 | 25/325 = 0,077 | 40 | 0,123 |
| Marzo | 40 | 40/325 = 0,123 | 80 | 0,246 |
| Abril | 35 | 35/325 = 0,108 | 115 | 0,354 |
| Mayo | 25 | 25/325 = 0,077 | 140 | 0,431 |
| Junio | 25 | 25/325 = 0,077 | 165 | 0,508 |
| Julio | 20 | 20/325 = 0,061 | 185 | 0,569 |
| Agosto | 45 | 45/325 = 0,138 | 230 | 0,707 |
| Septiembre | 35 | 35/325 = 0,108 | 265 | 0,815 |
| Octubre | 15 | 15/325 = 0,046 | 280 | 0,861 |
| Noviembre | 10 | 10/325 = 0,031 | 290 | 0,892 |
| Diciembre | 35 | 35/325 = 0,108 | 325 | 1 |
b)
La moda es el valor que más se repite. Como el mes en el que han nacido más alumnos ha sido agosto, significa que : Mo = Agosto
Media aritmética :
![]()


 INICIO
INICIO