Problemas resueltos de longitud de arco de una curva
1) Calcula la longitud de la circunferencia de radio r .
2) Hallar la longitud del arco de la curva 9 y2 = 4 x3 comprendido entre los puntos de la curva de abscisa x = 0 y x = 3
3) Hallar la longitud del arco de curva y = ln(cos x) comprendido entre los valores x = 0 y x = π/2
4) Hallar la longitud del arco de curva de la función
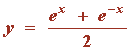
comprendido entre los valores x = - 1 y x = + 1
5) Hallar la longitud del arco de curva de la función
24xy - x4 - 48 = 0
comprendido entre los valores x = 2 y x = 4
1) Calcula la longitud de la circunferencia de radio r .
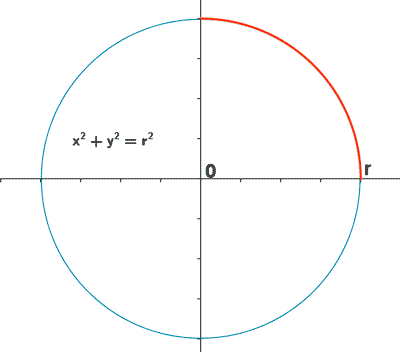
La ecuación de la curva que describe el cuadrante superior derecho es:
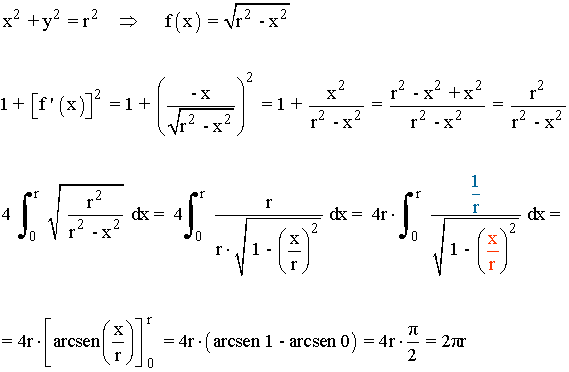
2) Hallar la longitud del arco de la curva 9 y2 = 4 x3 comprendido entre los puntos de la curva de abscisa x = 0 y x = 3
En este caso vemos que es sencillo expresar a y como función de x:
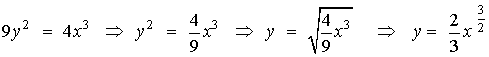
Derivando,
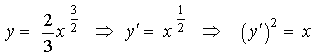
de manera que
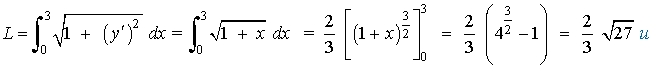
3) Hallar la longitud del arco de curva y = ln(cos x) comprendido entre los valores x = 0 y x = π/2
Empezamos calculando y' y su cuadrado:
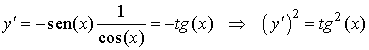
Teniendo esto en cuenta, la longitud de arco que nos piden es:
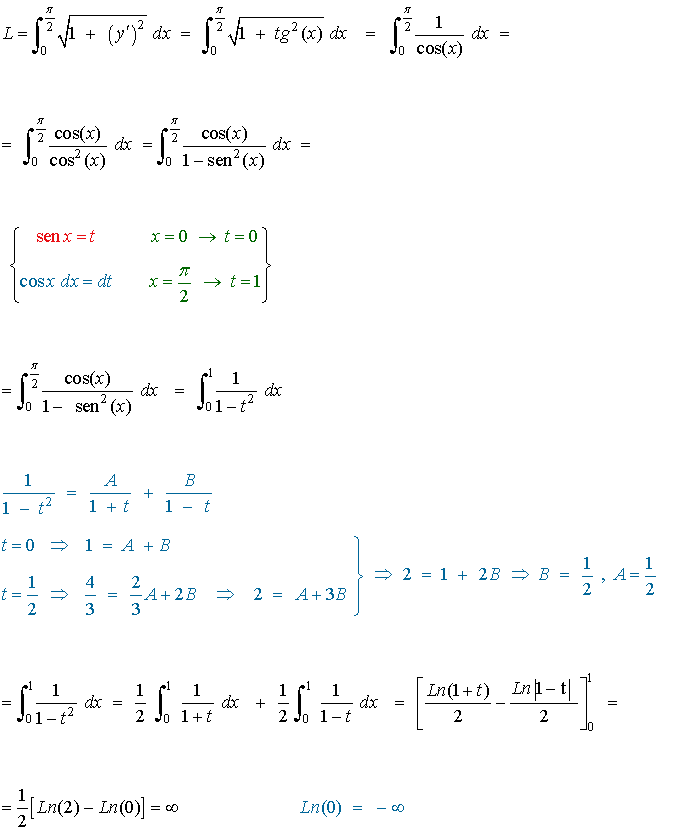
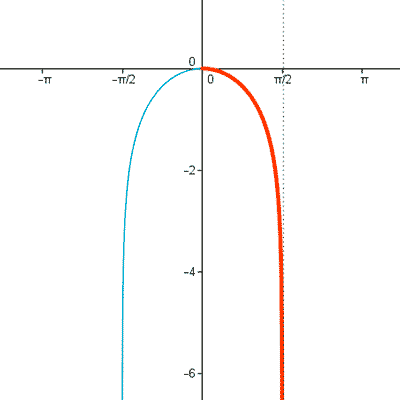
4) Hallar la longitud del arco de curva de la función
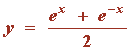
comprendido entre los valores x = - 1 y x = + 1
Recordamos que
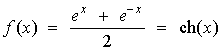
de manera que f '(x) = sh(x), y resulta que
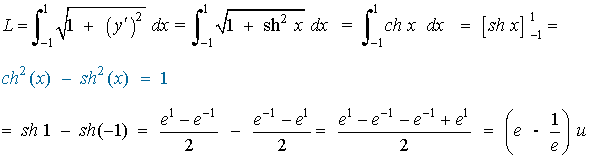
5) Hallar la longitud del arco de curva de la función
24xy - x4 - 48 = 0
comprendido entre los valores x = 2 y x = 4
Despejando la variable y podemos obtener la ecuación explícita de la curva que es
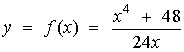
de manera que, derivando,
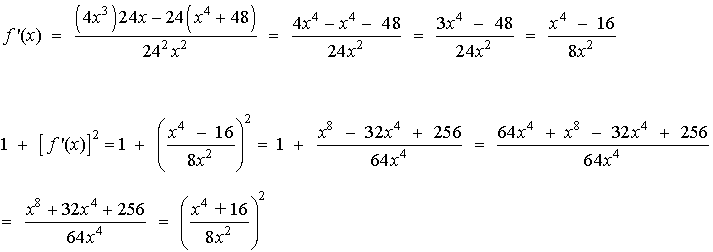
Teniendo esto en cuenta,
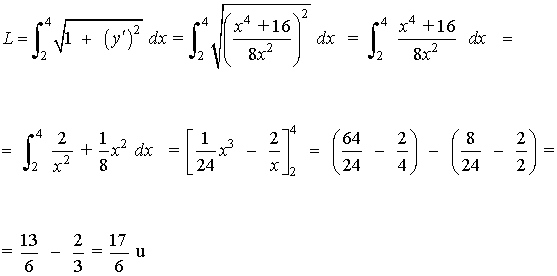


 INICIO
INICIO