Problemas y ejercicios de continuidad II
Estudia la continuidad de las siguientes funciones y dibújalas:
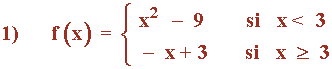
Como las funciones que definen f son continuas, los únicos puntos donde podría haber problema es en el de abscisa: x = 3
f(3) = - 3 + 3 = 0
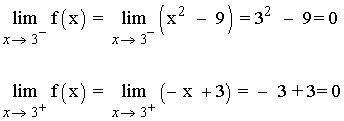
Como los límites laterales coinciden tenemos que:
![]()
Entonces:
![]()
Luego la función es continua también en x = 3.
La función f es continua en todo R .
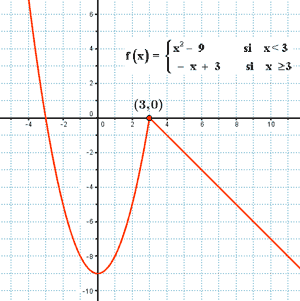
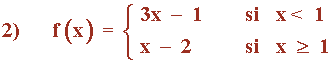
Como las funciones que definen f son continuas, los únicos puntos donde podría haber problema es en el de abscisa: x = 1
f(1) = 1 - 2 = - 1
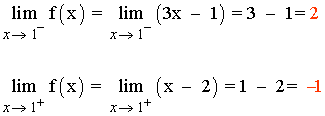
Como los límites laterales no coinciden tenemos que:
![]()
Y por tanto la función f es discontinua en el punto x = 1
Es una discontinuidad de primera especie o de salto finito.
La función f es continua en: R - {1}
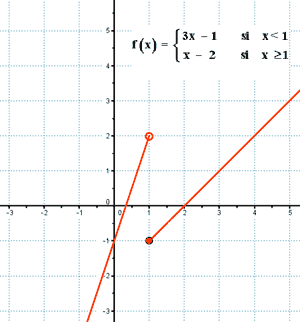
Estudia la continuidad de la siguiente función y dibújala:
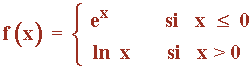
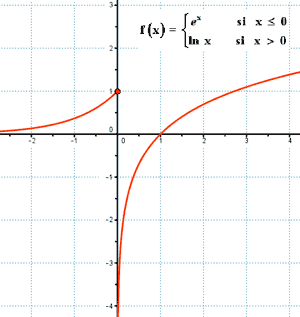
Como las funciones que definen f son continuas, los únicos puntos donde podría haber problema es en el de abscisa: x = 0
f(0) = e0 = 1
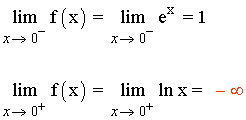
Uno de los límites laterales es -∞,
por tanto, la función f tiene una discontinuidad
de primera especie o de salto infinito en el punto x = 0 .
La función f es continua en: R - {0}
Estudia la continuidad de la siguiente función y dibújala:
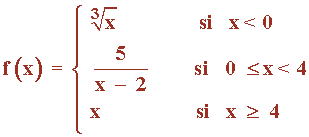
La primera y tercera ramas de la función están bien definidas en todo R .
Veamos el dominio de la segunda rama:
x - 2 = 0 ⇔ x = 2
Su dominio es R - {2}
Por tanto: Dom f = R - 2
Tenemos que estudiar la continuidad de la función en los puntos: x = 0 , x = 2 , x = 4
x = 0
f(0) = - 5/2
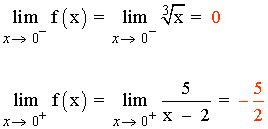
Como los límites laterales no coinciden tenemos que:
![]()
Y por tanto la función f es discontinua en el punto x = 0
Es una discontinuidad de primera especie o de salto finito.
x = 2
f(2) no existe
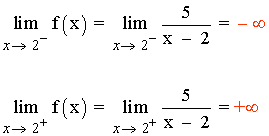
La función f es discontinua en el punto x = 2 .
Es una discontinuidad de primera especie o de salto infinito.
x = 4
f(4) = 4
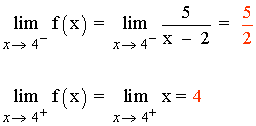
Como los límites laterales no coinciden tenemos que:
![]()
Y por tanto la función f es discontinua en el punto x = 4
Es una discontinuidad de primera especie o de salto finito.
Luego la función es continua en: R - {0 , 2 , 4}
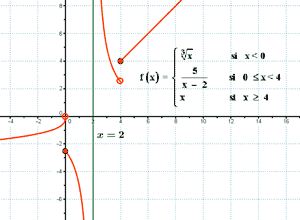
Estudia la continuidad de la siguiente función en el punto x = 4 :
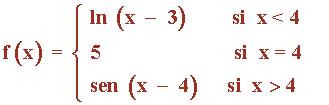
f(4) = 5
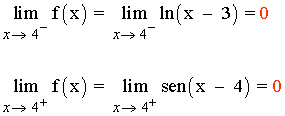
Como los límites laterales coinciden tenemos que:
![]()
Sin embargo:
![]()
Luego la función no es continua en x = 4 .
SELECTIVIDAD
¿Cuáles de las siguientes funciones son continuas en un entorno del punto cero?
![]()
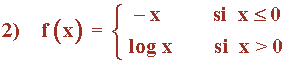
1) f(x) = 2-x
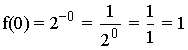
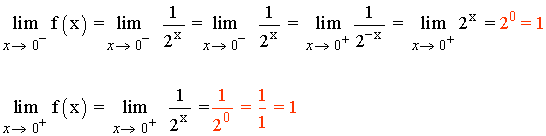
Como los límites laterales coinciden tenemos que:
![]()
Tenemos que:
![]()
Luego la función es continua en x = 0 .
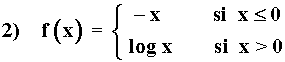
f(0) = 0
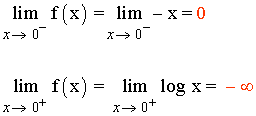
La función f es discontinua en x = 0 .
Como uno de los límites laterales es -∞ la discontinuidad es de primera especie o de salto infinito.
Considera la siguiente función y halla:
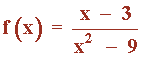
a) El dominio de la función, los puntos de corte con los ejes y las simetrías.
b) Los puntos donde la función no es continua, indicando el tipo de discontinuidad.
c) Las asíntotas.
d) Esboza la gráfica.
a) Dominio, puntos de corte con los ejes, simetrías.
Es una función racional, por tanto, para ver su dominio calculamos los puntos que anulan el denominador:
x2 - 9 = 0 ⇔ x2 = 9 ⇔ x = ±√9 = ± 3
Dom(f) = R - {-3 , +3}
Punto de corte con el eje de ordenadas:
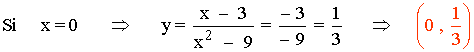
Punto de corte con el eje de abscisas:
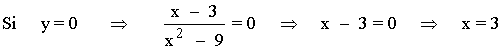
Pero x = 3 ∉ Dom(f) , por lo que la función no corta al eje de abscisas.
Estudiamos las simetrías de la función:
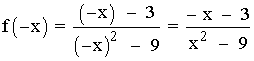
f(-x) ≠ f(x) , no tiene simetría par .
f(-x) ≠ - f(x) , no tiene simetría impar .
La función no tiene simetría.
b) Puntos de discontinuidad, tipo de discontinuidad.
La función es discontinua en aquellos puntos que no pertenecen a a su dominio: x = -3 , x = 3
x = - 3
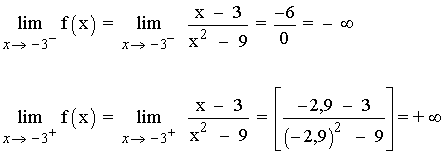
Como f(-3) no existe y el límite cuando x → -3 da ±∞ , la función f tiene una discontinuidad de primera especie o de salto infinito en el punto x = - 3 .
x = 3
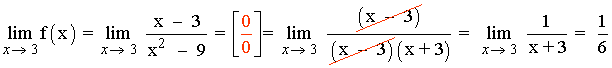
La función f tiene una discontinuidad evitable en x = 3 , pues f(3) no existe y el límite cuando x → 3 es finito.
c) Asíntotas.
Asíntotas verticales:
La función tiene una asíntota vertical en x = - 3 pues anula sólo al denominador.
En el punto x = 3 no hay asíntota vertical pues anula tanto al numerador como al denominador.
Asíntota horizontal:
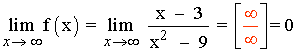
Hay una asíntota horizontal en: y = 0
Asíntotas oblicuas: como tiene asíntota horizontal, no tiene oblicuas.
d) Esboza la gráfica.
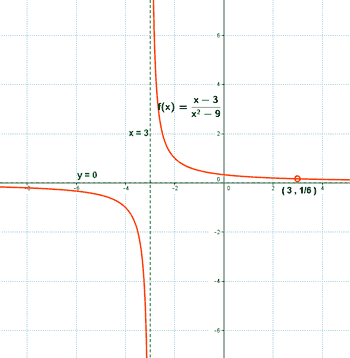
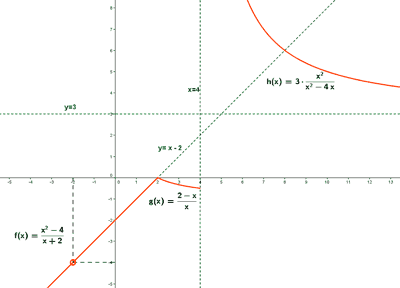
Dada la siguiente función:
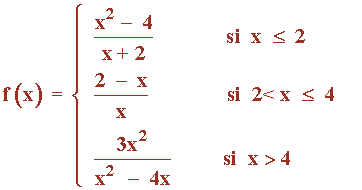
a) Determina su dominio.
b) Estudia la continuidad.
c) Halla las asíntotas.
a) Determina su dominio.
Hallamos el dominio para cada rama de la función.
Para ello calculamos las raíces de los denominadores teniendo en cuenta su intervalo de definición:
• En la primera rama: x + 2 = 0 ⇔ x = - 2 , y observamos que -2 ∈ (-∞ , 2] ⇒ -2 ∉ Dom(f)
• En la segunda rama: x = 0 , y observamos que 0 ∉ (2 , 4] , es decir, no está en el dominio de esta rama.
• En la tercera rama: x2 - 4x = 0 ⇔ x(x - 4) = 0 ⇔ x = 0 ó x = 4
y observamos que 0 , 4 ∉ (4 , ∞) , es decir, no están en el dominio de esta rama.
Por tanto: Dom(f) = R - {-2}
b) Estudia la continuidad.
Estudiamos la continuidad de la función en los puntos que no son del dominio y en los puntos de unión de cada rama: x = -2 , x = 2 , x = 4
x = - 2
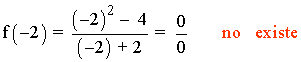
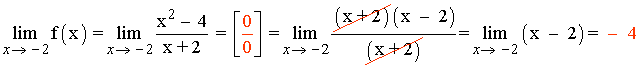
La función f tiene una discontinuidad evitable en x = -2 .
Para evitar la discontinuidad basta con determinar: f(-2) = - 4
x = 2
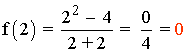
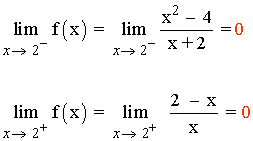
Como los límites laterales coinciden:
![]()
Además, observamos que:
![]()
Luego f es continua en x = 2 .
x = 4
![]()
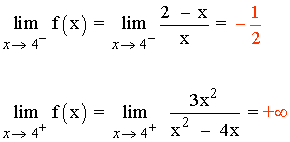
Uno de los límites laterales es +∞, por tanto, la función f tiene una discontinuidad de primera especie o de salto infinito en el punto x = 4 .
Conclusión: La función f es continua en R - {-2 , 4}
c) Halla las asíntotas.
Asíntotas verticales:
La única discontinuidad asintótica de la función es x = 4 .
Para ver el comportamiento de la función cuando se acerca a la asíntota x = 4 nos fijamos en los límites laterales calculados anteriormente:
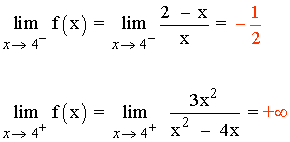
Asíntotas horizontales:
Tenemos que calcular el límite de f(x) cuando x → ±∞
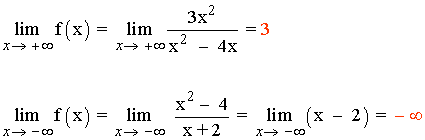
Hay una asíntota horizontal en y = 3 .
Cuando x→ -∞ no existe asíntota horizontal, así que vamos a ver si existe una asíntota oblicua.
Asíntotas oblicuas:
Tenemos que calcular una recta del tipo y = mx + n cuando x → -∞ , donde:
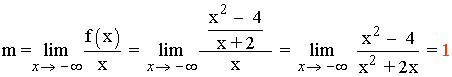
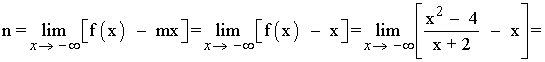
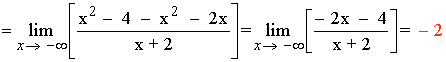
Por tanto, la función f tiene una asíntota oblicua en: y = x - 2


 INICIO
INICIO