Ejercicios resueltos de asíntotas I
Relaciona las gráficas con su función correspondiente sabiendo que todas tienen una asíntota vertical en x = -2 :
a)
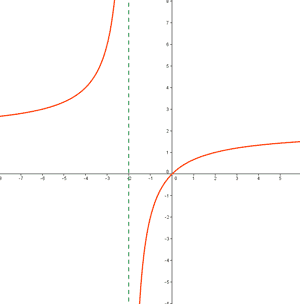
b)
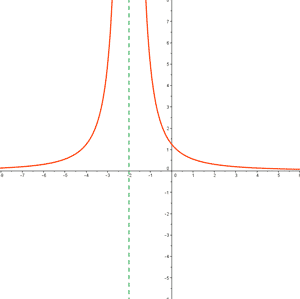
c)
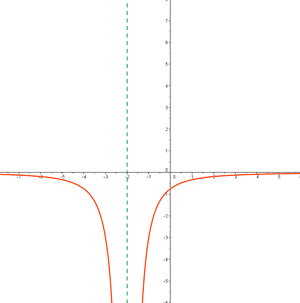
d)
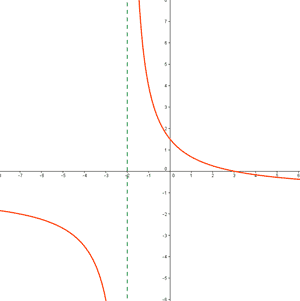
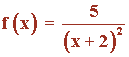
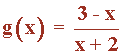
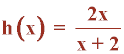
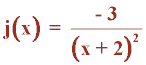
Observamos que todas las gráficas tienen una asíntota vertical en x = -2. Y además en cada caso, los límites laterales cuando x → -2 son distintos.
Por tanto, podremos asociar cada función a su gráfica según los límites laterales en x = -2 .
Calculamos pues, los límites laterales en x = -2 de cada función:

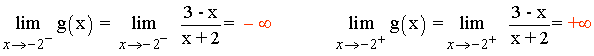


a) Por la izquierda de -2 la función va hacia +∞ , y por la derecha va hacia -∞ .
Por tanto, se corresponde con la función h(x).
b) Siguiendo el mismo razonamiento, podemos asegurar que se corresponde con la función f(x).
c) Se trata de la función j(x) .
d) Es la función g(x).
Halla las asíntotas de las siguientes funciones y esboza sus gráficas:
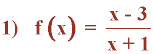
• Intervalos de signo constante:
Para estudiar los intervalos de signo constante tenemos que hallar los valores que anulan al numerador y al denominador:
Numerador: x - 3 = 0 ⇒ x = 3
Denominador: x + 1 = 0 ⇒ x = -1
Por lo tanto, los intervalos de signo constante son:
(-∞, -1) ⇒ f(-2) = -5/-1 = 5 > 0 ⇒ La función toma valores positivos en este intervalo
(-1, +3) ⇒ f(0) = -3/+1 = -3 < 0 ⇒ La función toma valores negativos en este intervalo
(+3, +∞) ⇒ f(4) = +1/+5 > 0 ⇒ La función toma valores positivos en este intervalo
• Asíntota vertical:
Las asíntotas verticales corresponden a los valores que anulan al denominador y no anulan al numerador. En este caso ocurre para x = -1 .
Para conocer la posición de la curva respecto a la asíntota, calculamos los límites laterales:
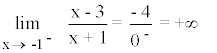
Por lo tanto, a la izquierda de x = -1 la curva tiende a infinito.
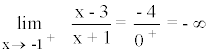
Es decir, a la derecha de x = -1 la curva tiende a menos infinito.
• Asíntota horizontal:
Para calcular las asintotas horizontales calculamos el límite de la función en el infinito.
![]()
A continuación calculamos la posición de la curva respecto a la asíntota:
Si el límite tiende a 0+ la curva está encima y si tiende a 0- está debajo.
![]()
Por lo tanto la curva queda por encima de la asíntota horizontal.
![]()
Por lo tanto la curva queda por debajo de la asíntota horizontal.
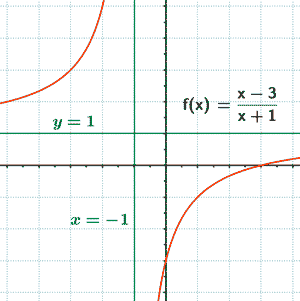
• Asíntota oblicua:
No tiene asíntotas oblicuas porque el grado del numerador no es uno más que el del denominador.
Además tiene una asíntota horizontal, por lo que no puede tener asíntotas oblicuas.
Halla las asíntotas de las siguientes funciones y esboza sus gráficas:
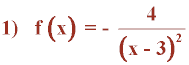
• Intervalos de signo constante:
Para estudiar los intervalos de signo constante tenemos que hallar los valores que anulan al numerador y al denominador:
Numerador: No se anula
Denominador: (x - 3)2 = 0 ⇒ x - 3 = 0 ⇒ x = 3
Por lo tanto, los intervalos de signo constante son:
(-∞, +3) ⇒ f(0) = -4/+9 < 0 ⇒ La función toma valores negativos en este intervalo
(+3, +∞) ⇒ f(4) = -4/+1 < 0 ⇒ La función toma valores negativos en este intervalo
• Asíntota vertical:
Las asíntotas verticales corresponden a los valores que anulan al denominador y no anulan al numerador. En este caso ocurre para x = 3 .
Para conocer la posición de la curva respecto a la asíntota, calculamos los límites laterales:
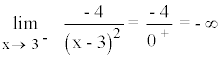
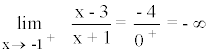
Tanto por la izquierda como por la derecha de x = 3 la curva tiende a menos infinito.
• Asíntota horizontal:
Para calcular las asintotas horizontales calculamos el límite de la función en el infinito.
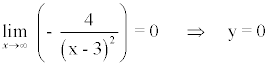
A continuación calculamos la posición de la curva respecto a la asíntota:
Si el límite tiende a 0+ la curva está encima y si tiende a 0- está debajo.
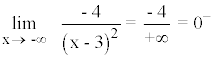
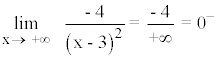
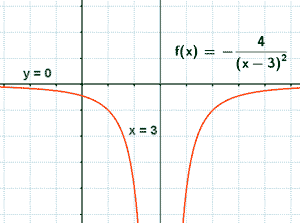
Por lo tanto la curva queda en todo momento por debajo de la asíntota horizontal.
• Asíntota oblicua:
No tiene asíntotas oblicuas porque el grado del numerador no es uno más que el del denominador.
Además tiene una asíntota horizontal, por lo que no puede tener asíntotas oblicuas.
Halla las asíntotas de las siguientes funciones y esboza sus gráficas:
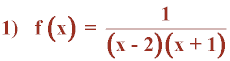
• Intervalos de signo constante:
Para estudiar los intervalos de signo constante tenemos que hallar los valores que anulan al numerador y al denominador:
Numerador: No se anula
Denominador: x = -1 y x = +2
Por lo tanto, los intervalos de signo constante son:
(-∞, -1) ⇒ f(-3) = 1/+10 > 0 ⇒ La función toma valores positivos en este intervalo
(-1, +2) ⇒ f(0) = 1/-2 < 0 ⇒ La función toma valores negativos en este intervalo
(+2, +∞) ⇒ f(3) = 1/+4 > 0 ⇒ La función toma valores positivos en este intervalo
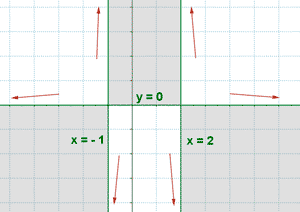
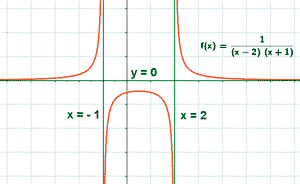
• Asíntota vertical:
Las asíntotas verticales corresponden a los valores que anulan al denominador y no anulan al numerador. En este caso ocurre para x = - 1 y x = 2 .
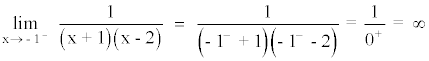
A la izquierda de x = -1 tiende a infinito.
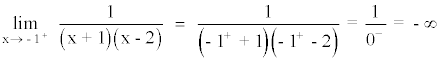
A la derecha de x = -1 tiende a menos infinito.
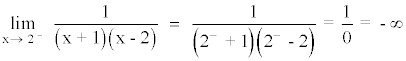
A la izquierda de x = 2 tiende a menos infinito.
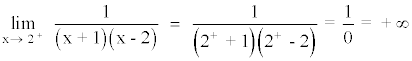
A la derecha de x = 2 tiende a infinito.
• Asíntota horizontal:
Para calcular las asintotas horizontales calculamos el límite de la función en el infinito.
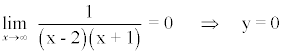
A continuación calculamos la posición de la curva respecto a la asíntota:
Si el límite tiende a 0+ la curva está encima y si tiende a 0- está debajo.
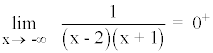
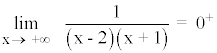
Por lo tanto la curva queda en todo momento por encima de la asíntota horizontal cuando x → ±∞
• Asíntota oblicua:
No tiene asíntotas oblicuas porque el grado del numerador no es uno más que el del denominador.
Además tiene una asíntota horizontal, por lo que no puede tener asíntotas oblicuas.
Halla las asíntotas de las siguientes funciones y esboza sus gráficas:
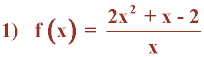
• Intervalos de signo constante:
Para estudiar los intervalos de signo constante tenemos que hallar los valores que anulan al numerador y al denominador:
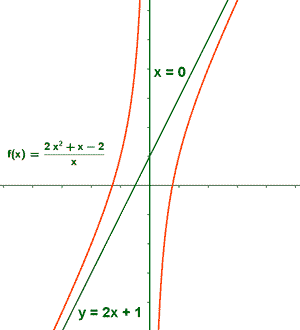
Numerador: 2x2 + x - 2 = 0 ⇒ x1 ≈ -1,28 y x2 ≈ 0,78
Denominador: x = 0
Por lo tanto, los intervalos de signo constante son:
(-∞, -1,28) ⇒ f(-2) < 0 ⇒ La función toma valores negativos en este intervalo
(-1,28, 0) ⇒ f(-1) > 0 ⇒ La función toma valores positivos en este intervalo
(0, +0,78) ⇒ f(0,5) < 0 ⇒ La función toma valores negativos en este intervalo
(+0,78, +∞) ⇒ f(1) > 0 ⇒ La función toma valores positivos en este intervalo
• Asíntota vertical:
Las asíntotas verticales corresponden a los valores que anulan al denominador y no anulan al numerador. En este caso ocurre para x = 0 .
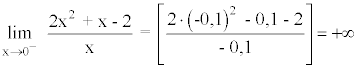
A la izquierda de x = 0 la función tiende a infinito.
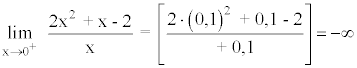
A la derecha de x = 0 la función tiende a menos infinito.
• Asíntota horizontal:
Para calcular las asintotas horizontales calculamos el límite de la función en el infinito.
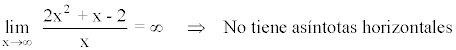
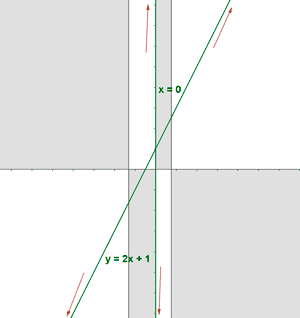
• Asíntotas oblicuas:
Para hallar las asíntotas oblicuas tenemos que calcular:
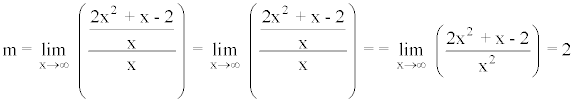
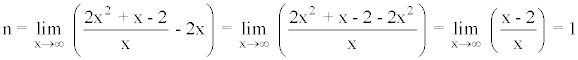
Por lo tanto existe una asíntota oblicua: y = 2x + 1
Para calcular la posición relativa respecto a la asíntota oblicua calculamos:
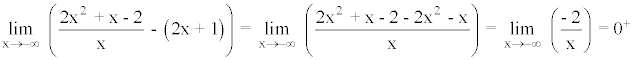
La curva está encima de la asíntota oblicua cuando la función tiende a menos infinito.
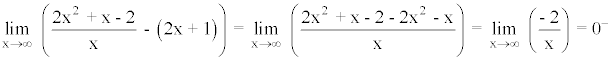
La curva está por debajo de la asíntota oblicua cuando la función tiende a infinito.
SELECTIVIDAD
La función y = f(x) tiene las siguientes propiedades:
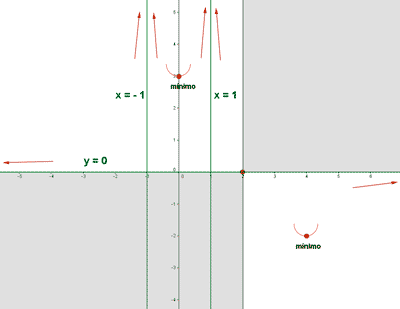
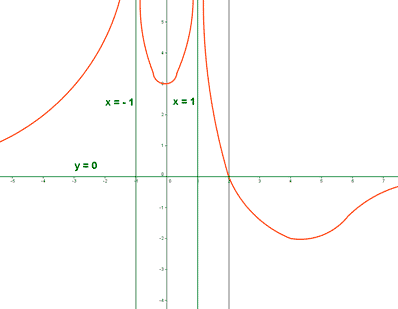
• Su dominio es la recta real salvo los puntos -1 y 1 . Es continua en todo su dominio. y corta al al eje X en el punto (2,0).
• Tiene una asíntota horizontal en y = 0 donde f(x) < 0 si x > 2 y f(x) > 0 si x < 2 ( x ≠ ±1 )
• Tiene una asíntota vertical en x = 1 , donde:
![]()
• Tiene una asíntota vertical en x = -1 , donde:
![]()
• Tiene un mínimo en el punto (4, -2) y otro en (0, 3). No tiene máximos.
a) Representa gráficamente dicha función.
b) Determina los intervalos de crecimiento y decrecimiento.
• Continuidad:
La función es continua en R - [-1, 1}.
• Puntos de corte:
La función corta al eje X en el punto (2, 0) y al eje Y en el punto (0, 3).
• Signo:
Como f(x) > 0 cuando x < 2 ⇒ La función toma valores positivos en el intervalo (-∞, 2) .
Como f(x) > 0 cuando x > 2 ⇒ La función toma valores negativos en el intervalo (2, +∞) .
• Máximos y mínimos:
La función tiene un mínimo en el punto (4, -2) y otro en el punto (0, 3) .
La función no tiene máximos.
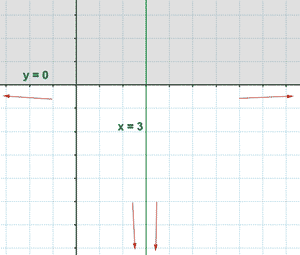
• Asíntotas verticales:
La función tiene dos asíntotas verticales en x = -1 y x = 1 .
Además, por los límites laterales sabemos que:
![]()
Cuando la función se acerca a -1 por la izquierda y por la derecha, la función tiende a +∞ .
![]()
Cuando la función se acerca a +1 por la izquierda y por la derecha, la función tiende a +∞ .
Estas tendencias se esbozan en la representación gráfica con flechas.
• Asíntotas horizontales:
La función tiene una asíntota horizontal en y = 0 .
Para saber si la gráfica queda por encima o por debajo de la asíntota, podemos estudiar el signo de la función:
Como f(x) > 0 cuando x < 2 ⇒ La gráfica está por encima de la asíntota cuando tiende a menos infinito.
Como f(x) > 0 cuando x > 2 ⇒ La gráfica está por debajo de la asíntota cuando tiende a infinito.
Al igual que en las asíntotas verticales, estas tendencias se esbozan en la representación gráfica con flechas.
SELECTIVIDAD
Considera las tres funciones cuyas expresiones respectivas vienen dadas, para x ≠ 0, por:
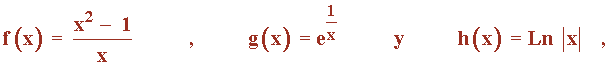
siendo Ln la funcíon logaritmo neperiano.
a) Halla las ecuaciones de las asíntotas de las gráficas de f , g y h.
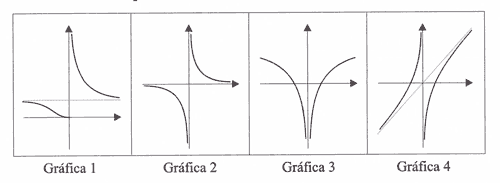
b) Identifica, entre las que siguen, la gráfica de cada función, justificando la respuesta.
a) Halla las ecuaciones de las asíntotas de las gráficas de f , g y h.
Función f:
Tiene asíntota vertical en los puntos que anulan el denominador: x = 0

No tiene asíntotas horizontales pues:
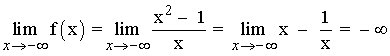
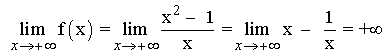
Como no tiene asíntotas horizontales, veamos si tiene oblicuas:
Realizamos la división: f(x) = x - 1/x
Luego la asíntota oblicua es y = x .
Situamos la gráfica con respecto a la asíntota:

Función g:
Tiene una asíntota vertical en x = 0 a la derecha del cero pues:
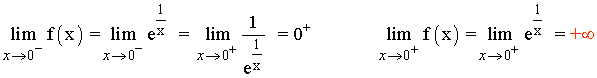
Veamos si tiene asíntotas horizontales:

Tiene una asíntota horizontal en y = 1 .
Función h:
Tiene asíntota vertical en x = 0 , por la derecha y por la izquierda del cero, pues:
![]()
La función logaritmo neperiano no tiene asíntotas horizontales ni oblicuas, por lo que tampoco las tiene la función h.
b) Identifica, entre las que siguen, la gráfica de cada función, justificando la respuesta.
Función f:
Tiene una asíntota vertical en x = 0.
Por lo visto en el apartado anterior, sabemos que cuando x → 0- el límite es +∞ y cuando x → 0+ da -∞ .
Además, tiene una asíntota oblicua en y = x .
La única gráfica que cumple dichas condiciones es la gráfica 4 .
Función g:
Tiene una asíntota en x = 0 , pero sólo por la derecha.
Además tiene una asíntota horizontal en y = 1.
La única gráfica que se corresponde con dichas condiciones es la gráfica 1.
Función h:
Tiene una asíntota en x = 0.
Hemos visto en el apartado anterior que cuando x → 0- y cuando x → 0 + el límite da, en ambos casos, - ∞.
La única gráfica que cumple dichos límites es la gráfica 3.


 INICIO
INICIO