Inecuaciones lineales con dos incógnitas
Una inecuación lineal o de primer grado con dos incógnitas es una desigualdad de uno de los siguientes tipos:

Llamamos coeficientes a los números reales a y b y término independiente al número real c.
Resuelve la siguiente inecuacion lineal:
2x - y ≥ - 3
Conjunto de soluciones de la primera inecuación:
2x - y = - 3 ⇔ y = 2x + 3
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 2x + 3 = 3 ⇒ A = (0 , 3)
y = 0 ⇒ 0 = 2x + 3 ⇒ x = - 3/2 ⇒ B = (- 3/2 , 0)
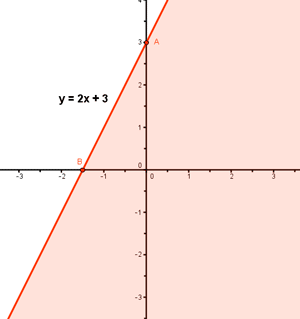
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , 2x - y ≥ - 3 ⇒ 0 ≥ - 3
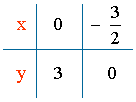
Sistemas de inecuaciones lineales con dos incógnitas
Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de n inecuaciones de primer grado de la forma:
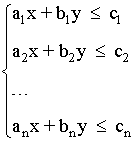
Llamamos coeficientes a los números reales ai y bi y términos independientes a los números reales ci.
La solución de un sistema de inecuaciones lineales con dos incógnitas es el conjunto de todos los puntos del plano que satisfacen todas sus inecuaciones.
La solución puede ser:
- Acotada: El conjunto de las soluciones está delimitado en todas sus direcciones.
- No acotada: El conjunto de las soluciones no está delimitado en alguna de sus direcciones.
Resuelve el siguiente sistema de inecuaciones lineales:
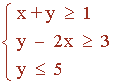
Conjunto de soluciones de la primera inecuación:
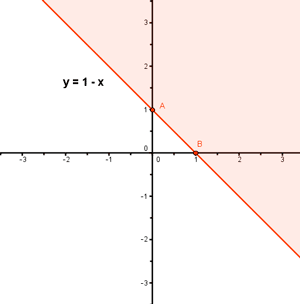
x + y = 1 ⇔ y = 1 - x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 1 - x = 1 ⇒ A = (0 , 1)
y = 0 ⇒ 0 = 1 - x ⇒ x = 1 ⇒ B = (1 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , x + y ≥ 1 ⇒ 0 ≥ 1 ¡no es cierto!
Probamos con otro punto del otro lado de la recta, por ejemplo:
(2 , 2) , x + y ≥ 1 ⇒ 4 ≥ 1
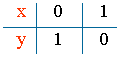
Conjunto de soluciones de la primera inecuación:
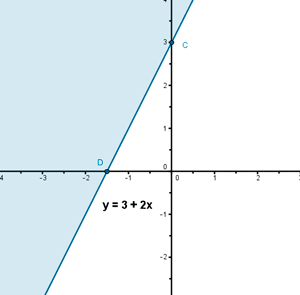
y - 2x = 3 ⇔ y = 3 + 2x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 3 + 2x = 3 ⇒ C = (0 , 3)
y = 0 ⇒ 0 = 3 + 2x ⇒ x = - 3/2 ⇒ D = (- 3/2 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , y - 2x ≥ 3 ⇒ 0 ≥ 3 ¡no es cierto!
Probamos con otro punto, por ejemplo:
(- 2 , 2) , y - 2x ≥ 3 ⇒ 6 ≥ 3
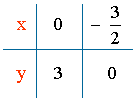
Conjunto de soluciones de la primera inecuación:
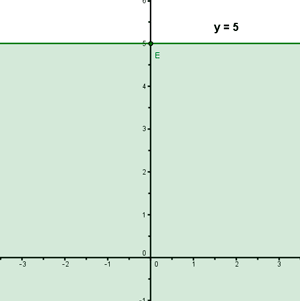
y = 5
La recta sólo corta al eje de abcisas: para cualquier valor de x siempre se tiene y = 5.
Por ejemplo, si x = 0 ⇒ (0 , 5)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , y ≤ 5 ⇒ 0 ≤ 5
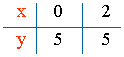
El conjunto de soluciones del sistema estará formado por aquellos valores de x que cumplan las tres inecuaciones, por tanto, la solución será la intersección de los tres semiplanos:
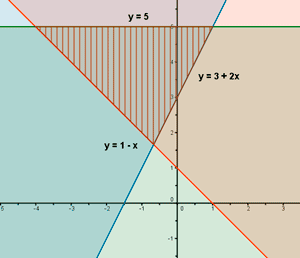
Solución acotada: El conjunto de las soluciones está delimitado en todas sus direcciones.


 INICIO
INICIO
