Problemas resueltos de Programación Lineal
• Dietas
1) Un ganadero debe suministrar un mínimo diario de 4 mg de vitamina A y 6 mg de vitamina B en el pienso que da a sus reses. Dispone para ello de dos tipos de pienso P1 y P2, cuyos contenidos vitamínicos por kilogramo son los que aparecen en la tabla:
| A | B | |
|---|---|---|
| P1 | 2 | 6 |
| P2 | 4 | 3 |
2) Para la elaboración de un alimento para el ganado, una empresa láctea puede adquirir dos productos básicos P1 y P2 y mezclarlos. La tabla siguiente muestra las unidades de nutrientes A, B y C que tiene cada kilogramo de P1 y P2, las cantidades de A, B y C necesarias para que el producto sea adecuado y el coste, en unidades monetarias, de cada kg de P1 y P2:
| A | B | C | Precio | |
|---|---|---|---|---|
| P1 | 2 | 2 | 1 | 3 |
| P2 | 1 | 2 | 3 | 2 |
| C. Mínima | 4 | 12 | 10 |
3) Un veterinario aconseja a un granjero dedicado a la cría de aves una dieta mínima que consiste en 3 unidades de hierro y 4 unidades de vitamina diarias. El granjero sabe que cada kilo de maiz proporciona 2.5 unidades de hierro y 1 de vitaminas y que cada kilo de pienso compuesto proporciona 1 de hierro y 2 de vitaminas. Sabiendo que el kilo de maiz vale 0.3 € y el de pienso compuesto 0,52€ se pide:
a) ¿Cuál es la composición de la dieta diaria que minimiza los costes del granjero? Explica los pasos seguidos para obtener la respuesta.
b) ¿Cambiaría la solución del problema si por escasez en el mercado el granjero no pudiera disponer de más de un kilo de pienso compuesto? Razona la respuesta
• Producción
4) Un orfebre fabrica dos tipos de joyas:
La unidad de tipo A se hace con 1 g de oro y 1,5 g de plata y se vende a 25€.
La de tipo B se vende a 30 € y lleva 1,5 g de oro y 1 g de plata.
Si solo se dispone de 750 g de cada metal, ¿cuántas joyas ha de fabricar de cada tipo para obtener el máximo beneficio?
Resolver análiticamente y gráficamente el problema
5) Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos.
Por necesidades del mercado es necesario que haya mayor o igual número de mecánicos que de electricistas y que el número de mecánicos no supere al doble del de electricistas. En total hay disponibles 30 electricistas y 20 mecánicos.
El beneficio de la empresa por jornada es de 150 € por electricista y 120 € por mecánico.
¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo beneficio?
6) Una confitería es famosa por sus dos especialidades en tartas: la tarta Imperial y la tarta de Lima.
La tarta Imperial requiere para su elaboración medio kilo de azúcar y 8 huevos, y tiene un precio de venta de 8€. La tarta de Lima necesita 1 kilo de azúcar y 8 huevos, y tiene un precio de venta de 10€. En el almacen quedan 10 kilos de azúcar y 120 huevos
a) ¿Qué combinaciones de especialidades pueden hacer?
b) ¿Cuántas unidades de cada especialidad han de producirse para obtener el mayor ingreso por ventas?
7) En un taller de confección se van a elaborar trajes de cocinero y de camarero. Se dispone para ello de 30 m2 de algodón, 10 m2 de fibra sintética y 20 m2 de lana. Para hacer cada traje de de cocinero se precisan 1 m2 de algodón, 2 m2 de fibra sintética y 2 m2 de lana. Cada unidad de este tipo deja 20 euros de beneficios. Para hacer cada traje de camarero se precisan 2 m2 de algodón, 1 m2 de fibra sintética y 1 m2 de lana. Cada unidad de este tipo deja 30 euros de beneficios. Se deben confeccionar mayor o igual número de trajes de camarero que de cocinero y, como mínimo se deben hacer un traje de cocinero y dos de camarero. El total no podrá ser superior a 20.
a) ¿Cuántos trajes de cada tipo se deberán confeccionar de manera que el beneficio sea máximo?
b) ¿Sobrará algún tipo de material?
c) ¿Hay alguna condición redundante?
8) Una empresa está seleccionando empleados con contrato eventual por un año y con contrato fijo. Sus sueldos anuales son, respectivamente, 8000 € y 15000€. La empresa tiene un tope máximo de 480000€ para los sueldos de estos nuevos empleados. El número de empleados fijos ha de estar entre 10 y 24. Los eventuales no pueden ser más de 14.
Si el objetivo es contratar al mayor número de empleados, ¿cuántos ha de contratar de cada tipo?
¿Y si el objetivo fuera contratar al mayor número de eventuales?
9) Un fabricante de muebles produce dos tipos de mesas clásicas y modernas. Cada mesa del modelo clásico requiere 4 horas de lijado y 3 horas de barnizado, y deja un beneficio de 200 €. No deben fabricarse más de 9 de estas mesas. Cada mesa moderna necesita 3 horas de lijado y 4 horas de barnizado, y su beneficio es de 100 €. Se dispone de 48 horas para lijado y de 60 horas para barnizado.
¿Cuántas mesas de cada tipo ha de fabricar para que sus beneficios sean máximos?
• Inversión
10) Una empresaria desea invertir los beneficios de 7500 euros obtenidos en su negocio en dos tipos de acciones, A y B. El tipo A produce un interés anual esperado del 6%, y el tipo B, del 4%. Como máximo desea invertir 5000 euros en A, y como mínimo, 1500 euros en B. Además, desea que la inversión en A sea superior a dos veces y media la inversión en B.
¿Cómo deberá realizar la inversión para que las ganancias sean máximas?
11) Una persona tiene 15000 € para invertir en dos tipos de acciones, A y B. El tipo A tiene un interés anual del 9% y el tipo B, del 5%.
Decide invertir, como máximo, 9000 € en A, y como mínimo, 3000 € en B. Además, quiere invertir en A tanto o más que en B.
a) Dibuja la región factible
b) ¿Cómo debe invertir los 15000 € para que el beneficio sea máximo?
c) ¿Cuál es ese beneficio anual máximo?
• Transporte
12) Una peña de aficionados de un equipo de fútbol encarga a una empresa de transportes el viaje para llevar a los 1200 socios a ver un partido de su equipo. La empresa disponde de autobuses de 50 plazas y de microbuses de 30 plazas. El precio de cada autobús es de 1260 € y el de cada microbús de 900 €. La empresa solo dispone, ese día, de 28 conductores.
¿Qué número de autobuses y microbuses deben contratarse para conseguir el mínimo coste posible? ¿Cuál es ese coste?
13) Una empresa compra 5 autobuses a una factoría francesa y 7 a una alemana. Quiere proveer al menos de 6 autobuses a la estación de Palma y al menos de 3 a la de Inca.
¿Cuántos autobuses de cada tipo colocará la empresa en cada estación si desea que el coste sea mínimo, siendo el coste del tipo de autobús, según destino, el indicado en la tabla?
| Francés | Alemán | |
|---|---|---|
| Palma | 4 | 16 |
| Inca | 9 | 17 |
• Geometría
14) Consideremos las mesas (rectangulares) cuyas dimensiones no sobrepasen (cada una) 2 m, y de entre ellas, la que la suma de su dimensión mayor y el doble de la menor no sobrepase 4m. Determinar el máximo valor que puede tener el perímetro de estas.
15) Considera el triángulo de vértices (0,0), (2,8) y (10,3). Determina razonadamente:
a) El punto del triángulo donde la función F(x,y) = -4x + y + 9 alcanza el máximo.
b) El punto del triángulo donde la función G(x,y) = 4x + y + 9 alcanza el máximo.
1) Un ganadero debe suministrar un mínimo diario de 4 mg de vitamina A y 6 mg de vitamina B en el pienso que da a sus reses. Dispone para ello de dos tipos de pienso P1 y P2, cuyos contenidos vitamínicos por kilogramo son los que aparecen en la tabla:
| A | B | |
|---|---|---|
| P1 | 2 | 6 |
| P2 | 4 | 3 |
Empezamos traduciendo el problema al lenguaje de la programación lineal:
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x a los kilogramos de pienso P1.
- Llamamos y a los kilogramos de pienso P2.
Queremos minimizar el coste del pienso es decir la función que nos permite calcular el dinero que gastamos en pienso. Dicha función es
F(x,y) = 0,4 x + 0,6 y
Las restricciones del problema son:
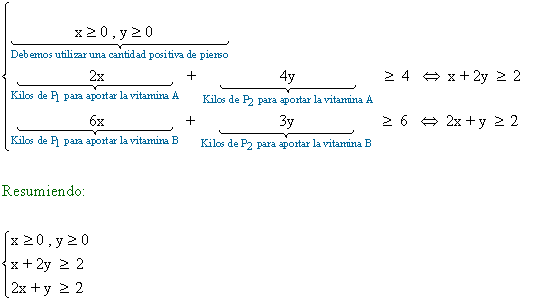
Teniendo todo esto en cuenta podemos pasar a la resolución del problema:
- Se representa gráficamente la región factible
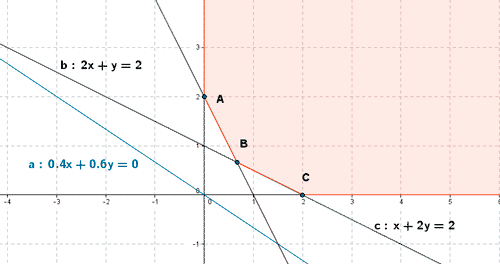
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
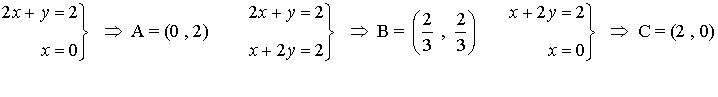
- Buscamos el mínimo de la función F y sabemos que dicho mínimo se alcanzará en alguno de los vértices anteriores de manera que calculamos el valor de F en dichos puntos:
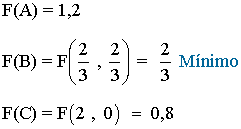
- El vértice que minimiza la función es el vértice B. Por tanto la forma más barata de asegurar el suministro de las dos vitaminas a las vacas es darles 2/3 de kilo de cada uno de los tipos de pienso.
2) Para la elaboración de un alimento para el ganado, una empresa láctea puede adquirir dos productos básicos P1 y P2 y mezclarlos. La tabla siguiente muestra las unidades de nutrientes A, B y C que tiene cada kilogramo de P1 y P2, las cantidades de A, B y C necesarias para que el producto sea adecuado y el coste, en unidades monetarias, de cada kg de P1 y P2:
| A | B | C | Precio | |
|---|---|---|---|---|
| P1 | 2 | 2 | 1 | 3 |
| P2 | 1 | 2 | 3 | 2 |
| C. Mínima | 4 | 12 | 10 |
Empezamos traduciendo el problema al lenguaje de la programación lineal:
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x a los kilogramos de pienso P1.
- Llamamos y a los kilogramos de pienso P2.
Queremos minimizar el coste del pienso es decir la función que nos permite calcular el dinero que gastamos en pienso. Dicha función es
F(x,y) = 3 x + 2 y
Las restricciones del problema son:

Teniendo todo esto en cuenta podemos pasar a la resolución del problema:
- Se representa gráficamente la región factible
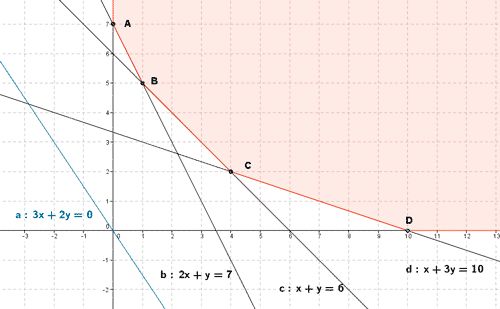
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
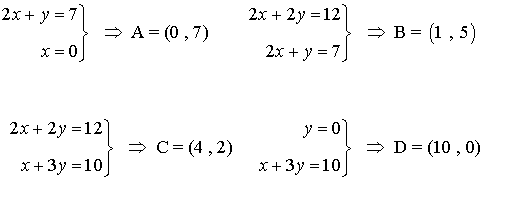
- Buscamos el mínimo de la función F y sabemos que dicho mínimo se alcanzará en alguno de los vértices anteriores de manera que calculamos el valor de F en dichos puntos:
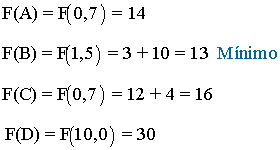
- El vértice que minimiza la función es el vértice B. Por tanto la forma más barata de asegurar el suministro de las tres sustancias vitaminas a las vacas es darles 1 kilo de pienso P1 y 5 kilos de pienso P2 y el coste será de 13 €
3) Un veterinario aconseja a un granjero dedicado a la cría de aves una dieta mínima que consiste en 3 unidades de hierro y 4 unidades de vitamina diarias. El granjero sabe que cada kilo de maiz proporciona 2.5 unidades de hierro y 1 de vitaminas y que cada kilo de pienso compuesto proporciona 1 de hierro y 2 de vitaminas. Sabiendo que el kilo de maiz vale 0.3 € y el de pienso compuesto 0,52€ se pide:
a) ¿Cuál es la composición de la dieta diaria que minimiza los costes del granjero? Explica los pasos seguidos para obtener la respuesta.
b) ¿Cambiaría la solución del problema si por escasez en el mercado el granjero no pudiera disponer de más de un kilo de pienso compuesto? Razona la respuesta
Empezamos resumiendo la información en un cuadro
| Hierro | Vitaminas | Precio | |
|---|---|---|---|
| Maiz | 2,5 | 1 | 0,3 € |
| Pienso | 1 | 2 | 0,52 € |
| C. Mínima | 3 | 4 |
Teniendo en cuenta esta tabla nos será más fácil traducir el problema al lenguaje de la programación lineal:
- Llamamos x a los kilos de maiz.
- Llamamos y a los kilos de pienso compuesto.
Queremos minimizar el coste, es decir, la función que nos permite calcular el dinero que cuesta alimientar a un ave. Dicha función es
F(x,y) = 0,3 x + 0,52 y
a)
Para el apartado a) Las restricciones del problema son:
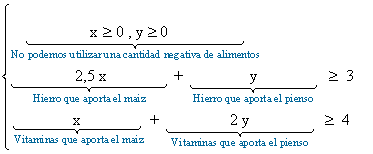
Utilizamos el método gráfico
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta 15 x + 26 y = 0 (que es la misma que 0,3 x + 0,52 y)
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
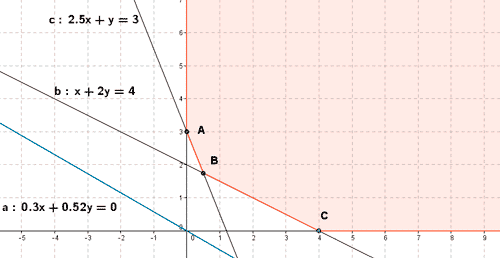
- Para la recta 15 x + 26 y = 0, tenemos que b > 0. Como queremos minimizar la función bastará con tomar el vértice por el cual pasa la paralela a 15 x + 26 y = 0 con menor ordenada en el origen. Dicho vértice es el vértice B. Por tanto la función objetivo alcanza su mínimo en el vértice B.
- Calculamos el vértice elegido en el paso anterior.
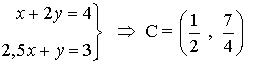
El vértice que minimiza la función es el vértice C. Por tanto habría que utilizar medio kilo de maiz y 7/4 kilos de pienso compuesto.
b)
En este apartado, a las restricciones del apartado a) se les añade otra más, que es que la cantidad de pienso de la que disponemos ha de ser menor o igual que un kilo, es decir y ≤ 1 de manera que las restricciones en este caso son
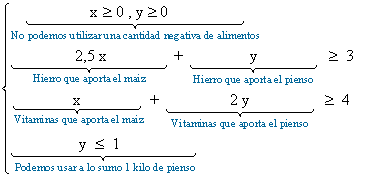
Utilizamos el método gráfico
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta 15 x + 26 y = 0 (que es la misma que 0,3 x + 0,52 y)
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
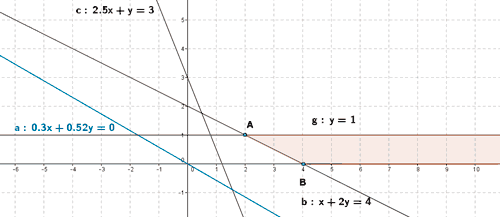
- Para la recta 15 x + 26 y = 0, tenemos que b > 0. Como queremos minimizar la función bastará con tomar el vértice por el cual pasa la paralela a 15 x + 26 y = 0 con menor ordenada en el origen. Dicho vértice es el vértice A. Por tanto la función objetivo alcanza su mínimo en el vértice A.
- Calculamos el vértice elegido en el paso anterior.
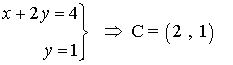
El vértice que minimiza la función es el vértice A. Por tanto habría que utilizar 2 kilos de maiz y 1 kilo de pienso compuesto. Como podemos observar, la restricción adicional cambia la solución obtenida en el apartado anterior.
4) Un orfebre fabrica dos tipos de joyas:
La unidad de tipo A se hace con 1 g de oro y 1,5 g de plata y se vende a 25€.
La de tipo B se vende a 30 € y lleva 1,5 g de oro y 1 g de plata.
Si solo se dispone de 750 g de cada metal, ¿cuántas joyas ha de fabricar de cada tipo para obtener el máximo beneficio?
Resolver análiticamente y gráficamente el problema
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x a la cantidad de joyas del tipo A.
- Llamamos y a la cantidad de joyas del tipo B.
Queremos maximizar el beneficio, es decir, la función que nos permite calcular el dinero obtenido de la venta de las joyas. Dicha función es
F(x,y) = 25 x + 30 y
Hacemos ahora un cuadro para facilitarnos el trabajo de establecer las restricciones:
| Tipo A | Tipo B | ||
|---|---|---|---|
| Oro | 1 g | 1,5 g | ≤ 750 g |
| Plata | 1,5 g | 1 g | ≤ 750 g |
Las restricciones del problema son:

Solución por el método analítico
- Se representa gráficamente la región factible
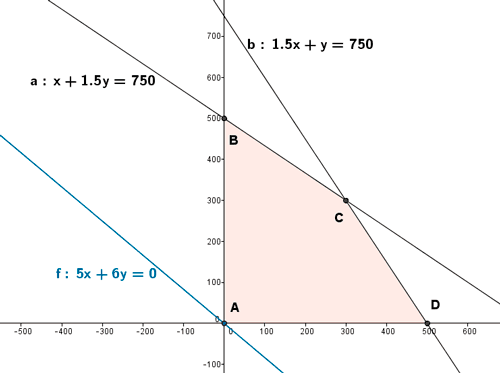
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
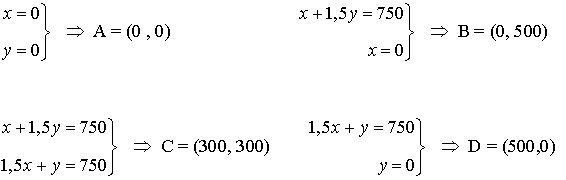
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
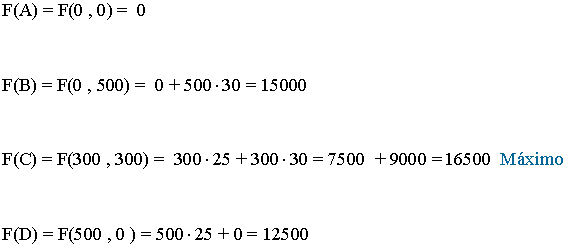
- El vértice que maximiza la función es el vértice C. Por tanto habría que fabricar 300 joyas de cada uno de los tipos y se venderían por 16500 €.
Solución por el método gráfico
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta 25 x + 30 y = 0.
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
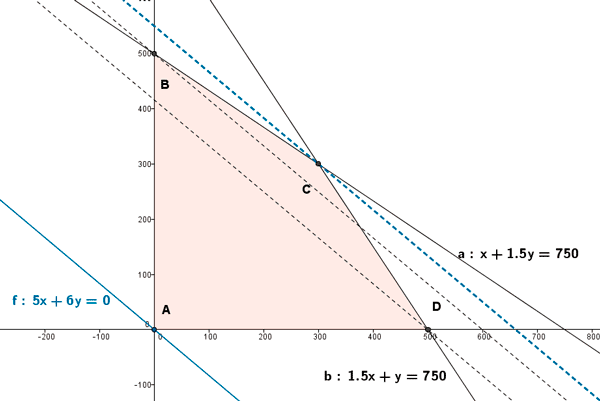
- Para la recta función objetivo F(x,y) = 25 x + 30 y, tenemos que b > 0. Como queremos maximizar la función bastará con tomar el vértice por el cual pasa la paralela a 25 x + 30 y = 0 con mayor ordenada en el origen. Dicho vértice es el vértice C. Por tanto la función alcanza su máximo en el vértice C.
- Calculamos el vértice elegido en el paso anterior.
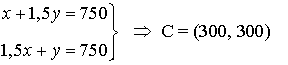
El vértice que maximiza la función es el vértice C. Por tanto habría que fabricar 300 joyas de cada uno de los tipos y, como F(300,300) = 16500, se venderían por 16500 €.
5) Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos.
Por necesidades del mercado es necesario que haya mayor o igual número de mecánicos que de electricistas y que el número de mecánicos no supere al doble del de electricistas. En total hay disponibles 30 electricistas y 20 mecánicos.
El beneficio de la empresa por jornada es de 150 € por electricista y 120 € por mecánico.
¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo beneficio?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de electricistas.
- Llamamos y a la cantidad de mecánicos.
Queremos maximizar el beneficio, es decir, la función que nos permite calcular el beneficio que genera el personal del taller. Dicha función es
F(x,y) = 150 x + 120 y
Las restricciones del problema son:

Solución por el método gráfico
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta 5 x + 4 y = 0 (que es equivalente a la recta 150 x + 120 y = 0).
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
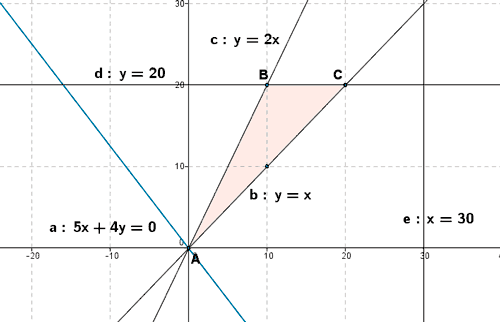
- Para F(x,y) = 5x + 4 y, tenemos que b > 0. Como queremos maximizar la función bastará con tomar el vértice por el cual pasa la paralela a 5 x + 4 y = 0 con mayor ordenada en el origen. Dicho vértice es el vértice C. Por tanto la función alcanza su máximo en el vértice C.
- Calculamos el vértice elegido en el paso anterior.
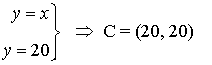
El vértice que maximiza la función es el vértice C. Por tanto habría que contratar 20 electricistas y 20 mecánicos.
6) Una confitería es famosa por sus dos especialidades en tartas: la tarta Imperial y la tarta de Lima.
La tarta Imperial requiere para su elaboración medio kilo de azúcar y 8 huevos, y tiene un precio de venta de 8€. La tarta de Lima necesita 1 kilo de azúcar y 8 huevos, y tiene un precio de venta de 10€. En el almacen quedan 10 kilos de azúcar y 120 huevos
a) ¿Qué combinaciones de especialidades pueden hacer?
b) ¿Cuántas unidades de cada especialidad han de producirse para obtener el mayor ingreso por ventas?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de tartas de tipo Imperial.
- Llamamos y a la cantidad de tartas de tipo Lima.
Las restricciones del problema son:
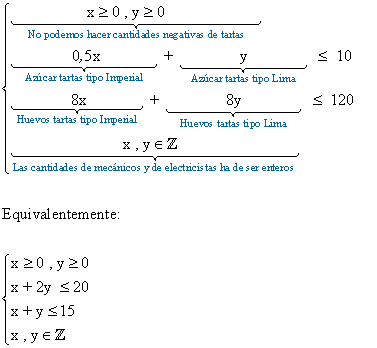
a)
Las posibles combinaciones de las dos especialidades de tartas que se pueden hacer con los ingredientes disponibles se corresponden con los puntos de coordenadas enteras dentro del recinto dado por las restricciones, incluyendo también la frontera:
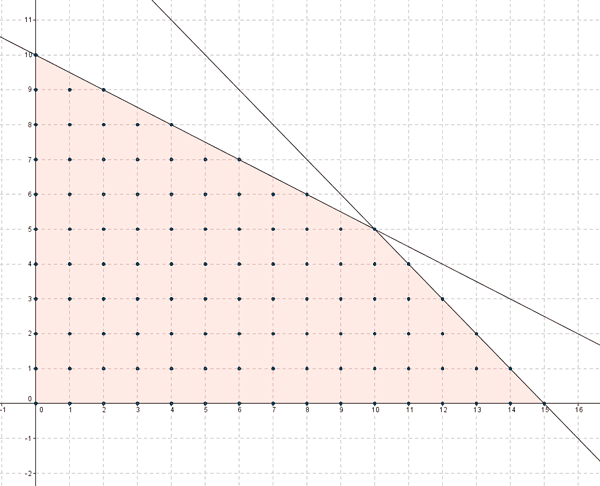
b)
Queremos maximizar los ingresos por la venta de las tartas, es decir, la función que nos permite calcular los ingresos que genera la venta de las tartas. Dicha función es
F(x,y) = 8 x + 10 y
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
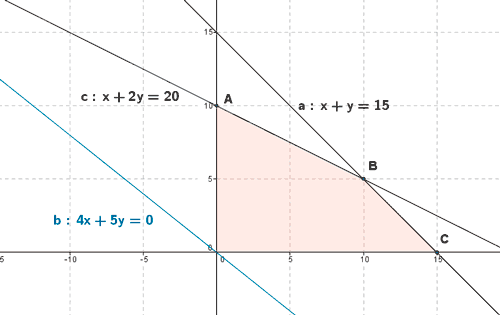
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
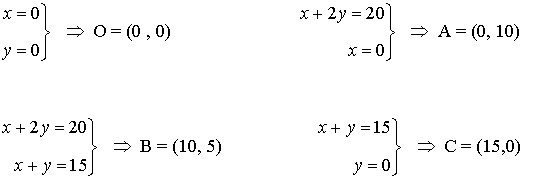
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
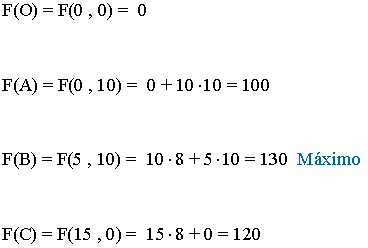
- El vértice que maximiza la función es el vértice B. Por tanto habría que fabricar 5 tartas de Lima y 10 tartas imperiales y se venderían por 130 €.
7) En un taller de confección se van a elaborar trajes de cocinero y de camarero. Se dispone para ello de 30 m2 de algodón, 10 m2 de fibra sintética y 20 m2 de lana. Para hacer cada traje de de cocinero se precisan 1 m2 de algodón, 2 m2 de fibra sintética y 2 m2 de lana. Cada unidad de este tipo deja 20 euros de beneficios. Para hacer cada traje de camarero se precisan 2 m2 de algodón, 1 m2 de fibra sintética y 1 m2 de lana. Cada unidad de este tipo deja 30 euros de beneficios. Se deben confeccionar mayor o igual número de trajes de camarero que de cocinero y, como mínimo se deben hacer un traje de cocinero y dos de camarero. El total no podrá ser superior a 20.
a) ¿Cuántos trajes de cada tipo se deberán confeccionar de manera que el beneficio sea máximo?
b) ¿Sobrará algún tipo de material?
c) ¿Hay alguna condición redundante?
a)
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de trajes de cocinero.
- Llamamos y a la cantidad de trajes de camarero.
Las restricciones del problema son:
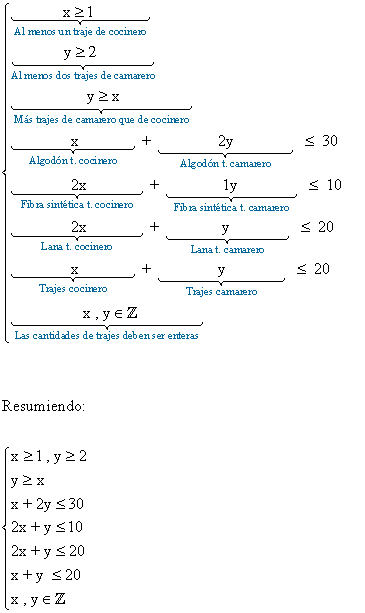
Queremos maximizar los ingresos por la venta de los trajes, es decir, la función que nos permite calcular los ingresos que genera la venta de los trajes. Dicha función es
F(x,y) = 20 x + 30 y
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
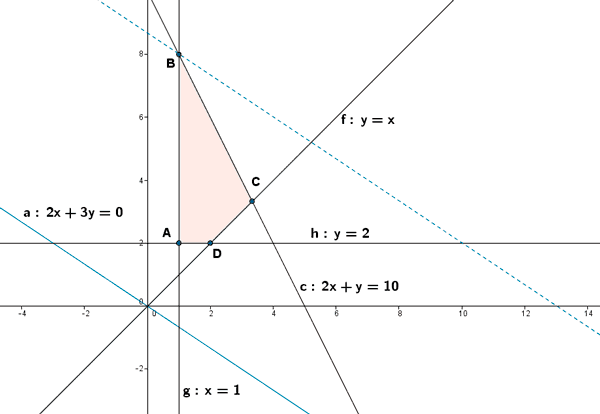
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
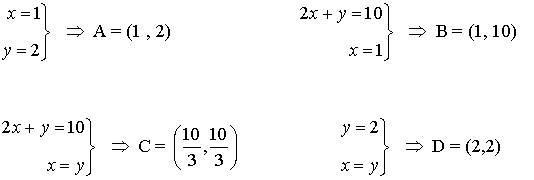
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
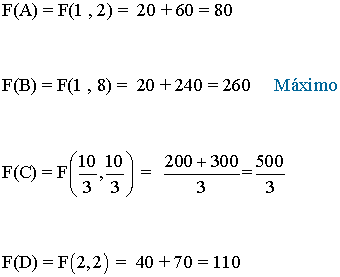
- El vértice que maximiza la función es el vértice B. Por tanto habría que fabricar 1 traje de cocinero y 8 de camarero obteniendo así unos ingresos de 260 €.
b)
Calculamos la diferencia entre los materiales utilizados y el material disponible:
| Algodón | Lana | Fibra Sintética | |
|---|---|---|---|
| 1 Traje de cocinero | 1 m2 | 2 m2 | 2 m2 |
| 8 Trajes de camarero | 16 m2 | 8 m2 | 8 m2 |
| TOTAL | 17 m2 | 10 m2 | 10 m2 |
| Material Disponible | 30 m2 | 20 m2 | 10 m2 |
| Material Sobrante | 13 m2 | 10 m2 | 0 m2 |
c)
Es claro que la condición 2x + y ≤ 20 es redundante ya que todo punto que satisface la inecuación 2x + y ≤ 10, que es otra de las condiciones, también verifica que 2x + y ≤ 20.
La condición x + y ≤ 20 también es redundante ya que por la cantidad de fibra sintética de la que disponemos, 10 metros, el mayor número de trajes que podríamos hacer (obviando las demás restricciones) es 10 trajes de camarero. Por tanto esta restricción siempre se verifica y es por ello redundante.
8) Una empresa está seleccionando empleados con contrato eventual por un año y con contrato fijo. Sus sueldos anuales son, respectivamente, 8000 € y 15000€. La empresa tiene un tope máximo de 480000€ para los sueldos de estos nuevos empleados. El número de empleados fijos ha de estar entre 10 y 24. Los eventuales no pueden ser más de 14.
Si el objetivo es contratar al mayor número de empleados, ¿cuántos ha de contratar de cada tipo?
¿Y si el objetivo fuera contratar al mayor número de eventuales?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de empleados fijos.
- Llamamos y al número de empleados eventuales.
Las restricciones del problema son:

En la primera pregunta nos piden maximizar el número de empleados contratados. Para ello debemos maximizar la función que calcula el número de empleados contratados que es:
F(x,y) = x + y
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
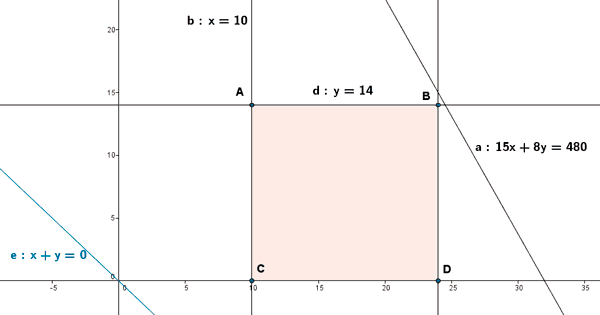
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
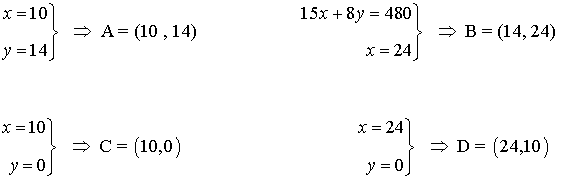
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
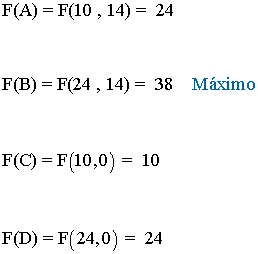
- El vértice que maximiza la función es el vértice B. Por tanto habría que contratar a 24 trabajadores fijos y 14 eventuales.
En la primera pregunta nos piden maximizar el número de empleados eventuales contratados. Para ello debemos maximizar la función que calcula el número de empleados eventuales contratados que es:
G(x,y) = y
Vamos a resolver el problema empleando el método analítico. Omitimos los dos primeros pasos porque se obtiene exactamente lo mismo que en la pregunta anterior:
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo

- Tanto en el vértice A como el vértice B se alcanza el máximo para la función objetivo G. Esto nos dice que dicha función alcanzará su máximo en todo el segmento AB. Por tanto la respuesta a la segunda pregunta es que pueden contratarse 14 empleados eventuales y entre 10 y 24 empleados fijos para contratar el máximo posible de empleados eventuales.
9) Un fabricante de muebles produce dos tipos de mesas clásicas y modernas. Cada mesa del modelo clásico requiere 4 horas de lijado y 3 horas de barnizado, y deja un beneficio de 200 €. No deben fabricarse más de 9 de estas mesas. Cada mesa moderna necesita 3 horas de lijado y 4 horas de barnizado, y su beneficio es de 100 €. Se dispone de 48 horas para lijado y de 60 horas para barnizado.
¿Cuántas mesas de cada tipo ha de fabricar para que sus beneficios sean máximos?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de mesas clásicas.
- Llamamos y al número de mesas modernas.
Las restricciones del problema son:
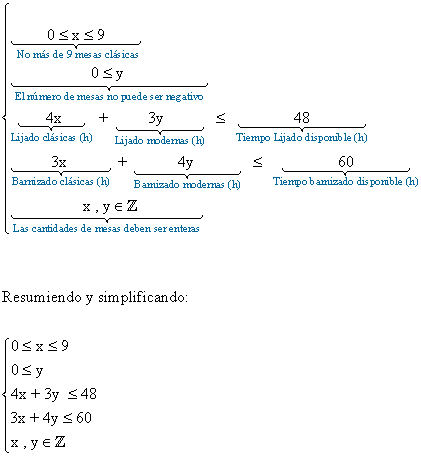
Se nos pide maximizar el beneficio. Para ello debemos maximizar la función que nos permite calcular dicho beneficio que es:
F(x,y) = 200x + 100y
Vamos a emplear el método gráfico para buscar el máximo de esta función:
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta 2 x + y = 0 (que es equivalente a la recta 200 x + 100 y = 0).
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
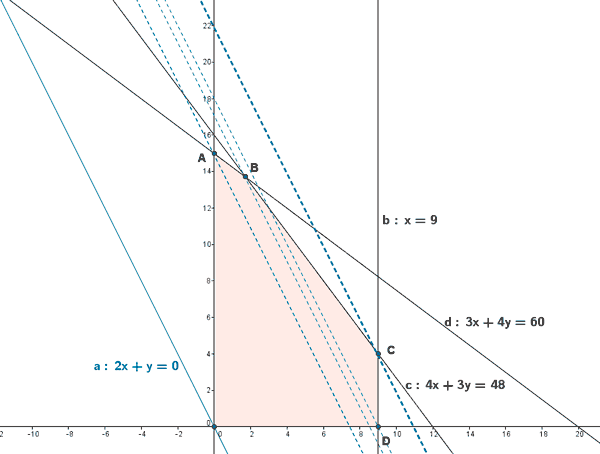
- Para la F(x,y) = 2x + y , tenemos que b > 0. Como queremos maximizar la función bastará con tomar el vértice por el cual pasa la paralela a 2x + y = 0 con mayor ordenada en el origen. Dicho vértice es el vértice C. Por tanto la función alcanza su máximo en el vértice C.
- Calculamos el vértice elegido en el paso anterior.
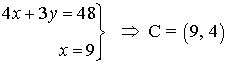
Como el vértice que maximiza la función es el vértice C, para obtener el máximo beneficio habría que fabricar 9 mesas clásicas y 4 mesas modernas.
10) Una empresaria desea invertir los beneficios de 7500 euros obtenidos en su negocio en dos tipos de acciones, A y B. El tipo A produce un interés anual esperado del 6%, y el tipo B, del 4%. Como máximo desea invertir 5000 euros en A, y como mínimo, 1500 euros en B. Además, desea que la inversión en A sea superior a dos veces y media la inversión en B.
¿Cómo deberá realizar la inversión para que las ganancias sean máximas?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al dinero invertido en acciones de tipo A.
- Llamamos y al dinero invertido en acciones de tipo B.
Las restricciones del problema son:
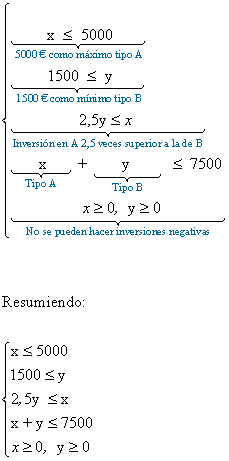
Nos piden maximizar el beneficio en la inversión. Para ello debemos maximizar la función que nos permite obtener el beneficio que es:
F(x,y) = 0,06x + 0,04y
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
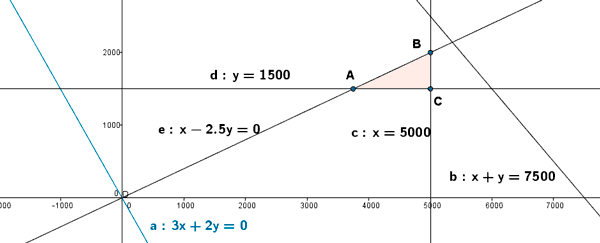
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
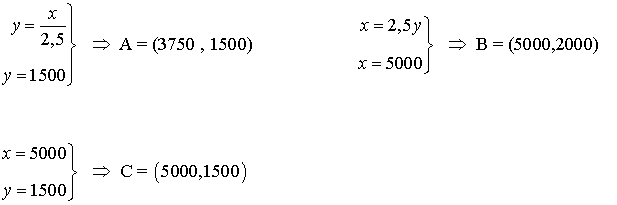
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
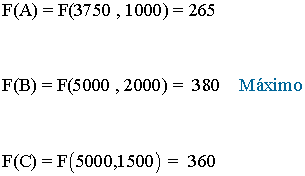
- El vértice que maximiza la función es el vértice B. Hay que invertir 5000 euros en acciones del tipo A y 2000 euros en acciones del tipo B. Los beneficios que se obtendrán de dicha inversión ascenderán a 380 euros.
11) Una persona tiene 15000 € para invertir en dos tipos de acciones, A y B. El tipo A tiene un interés anual del 9% y el tipo B, del 5%.
Decide invertir, como máximo, 9000 € en A, y como mínimo, 3000 € en B. Además, quiere invertir en A tanto o más que en B.
a) Dibuja la región factible
b) ¿Cómo debe invertir los 15000 € para que el beneficio sea máximo?
c) ¿Cuál es ese beneficio anual máximo?
a)
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al dinero invertido en acciones de tipo A.
- Llamamos y al dinero invertido en acciones de tipo B.
Las restricciones del problema son:
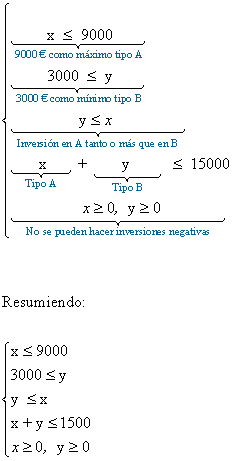
La región factible con estas restricciones sería la siguiente:
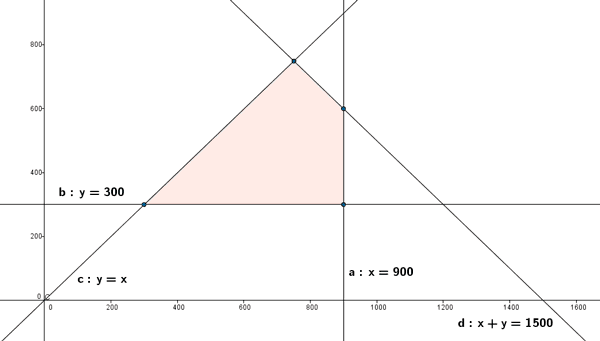
b)
Nos piden maximizar el beneficio en la inversión. Para ello debemos maximizar la función que nos permite obtener el beneficio que es:
F(x,y) = 0,09x + 0,05y
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
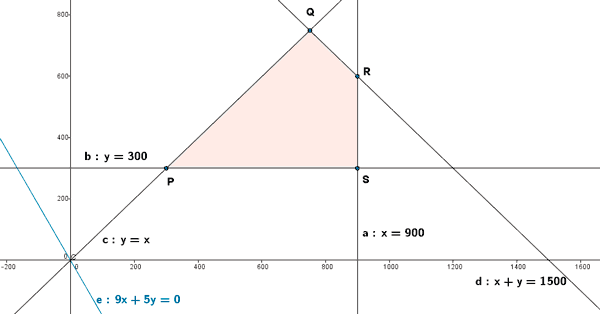
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
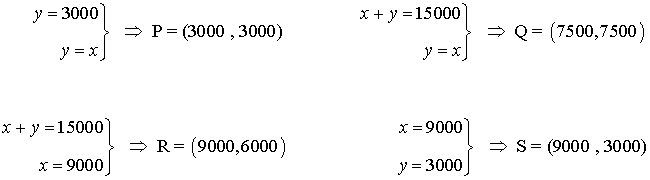
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
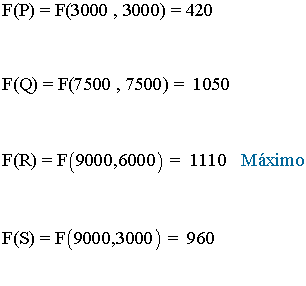
- El vértice que maximiza la función es el vértice R. Hay que invertir 9000 euros en acciones del tipo A y 6000 euros en acciones del tipo B.
c)
Los beneficios que se obtendrán de dicha inversión ascenderán a 1110 euros.
12) Una peña de aficionados de un equipo de fútbol encarga a una empresa de transportes el viaje para llevar a los 1200 socios a ver un partido de su equipo. La empresa disponde de autobuses de 50 plazas y de microbuses de 30 plazas. El precio de cada autobús es de 1260 € y el de cada microbús de 900 €. La empresa solo dispone, ese día, de 28 conductores.
¿Qué número de autobuses y microbuses deben contratarse para conseguir el mínimo coste posible? ¿Cuál es ese coste?
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al número de autobuses.
- Llamamos y al número de microbuses.
Las restricciones del problema son:

Nos piden minimizar el coste de la contratación del transporte. Para ello debemos minimizar la función que nos permite calcular dicho coste que es:
![]()
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
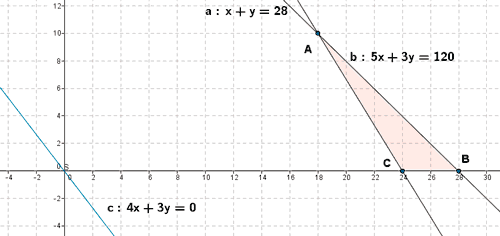
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
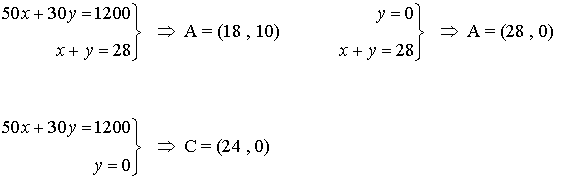
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo
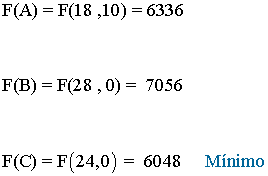
- El vértice que minimiza la función es el vértice C. Por tanto habrá que alquilar 24 autobuses y ningún microbus.
13) Una empresa compra 5 autobuses a una factoría francesa y 7 a una alemana. Quiere proveer al menos de 6 autobuses a la estación de Palma y al menos de 3 a la de Inca.
¿Cuántos autobuses de cada tipo colocará la empresa en cada estación si desea que el coste sea mínimo, siendo el coste del tipo de autobús, según destino, el indicado en la tabla?
| Francés | Alemán | |
|---|---|---|
| Palma | 4 | 16 |
| Inca | 9 | 17 |
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
| Francés | Alemán | |
|---|---|---|
| Palma | x | y |
| Inca | 5 - x | 7 - y |
Las restricciones del problema son:

Nos piden minimizar el coste de las líneas. Para ello debemos minimizar la función que nos permite calcular el coste de dichas líneas que es:
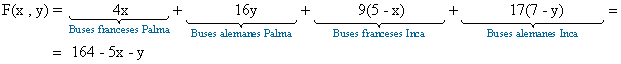
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
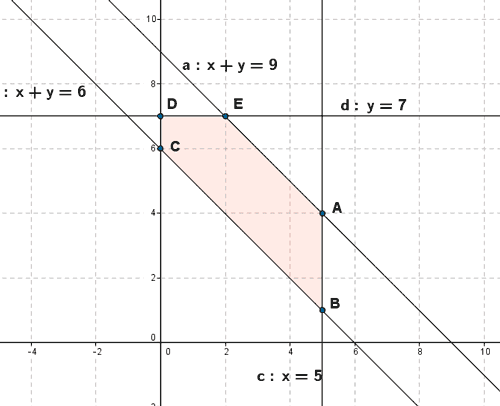
- Se calculan los vértices de la región factible. Dichos vértices serán las intersecciones de las rectas frontera de cada restricción que además verifiquen todas las restricciones.
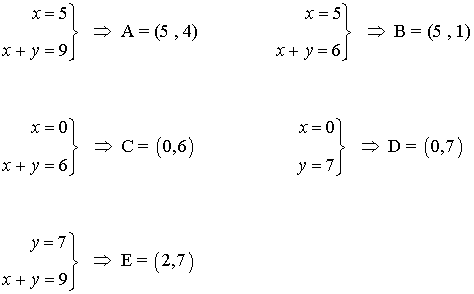
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo

- El vértice que minimiza la función es el vértice A. La asignación de autobuses deberá ser la siguiente:
| Francés | Alemán | |
|---|---|---|
| Palma | 5 | 4 |
| Inca | 0 | 3 |
14) Consideremos las mesas (rectangulares) cuyas dimensiones no sobrepasen (cada una) 2 m, y de entre ellas, la que la suma de su dimensión mayor y el doble de la menor no sobrepase 4m. Determinar el máximo valor que puede tener el perímetro de estas.
Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al tamaño de uno de los lados en metros.
- Llamamos y al la longitud del otro lado también en metros.
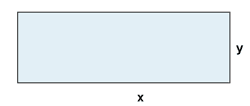
Las restricciones del problema son:
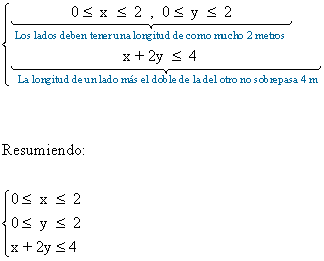
Nos piden maximizar el perímetro. Para ello debemos minimizar la función que nos permite calcular dicho perímetro, que es:
F(x,y) = 2x + 2y
Vamos a emplear el método gráfico para buscar el máximo de esta función:
| F(x,y) = ax + by | Maximizar | Minimizar |
|---|---|---|
| b > 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene mayor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen |
| b < 0 | El máximo es, si existe, el vértice cuya línea de nivel tiene menor ordenada en el origen | El mínimo es, si existe, el vértice cuya línea de nivel recta tiene mayor ordenada en el origen |
- Se representa la recta x + y = 0 (que es equivalente a la recta 2x + 2y = 0).
- Se trazan rectas paralelas a esta recta que pasen por cada uno de los vértices de la región factible. Tras los dos primeros pasos obtenemos la siguiente representación gráfica:
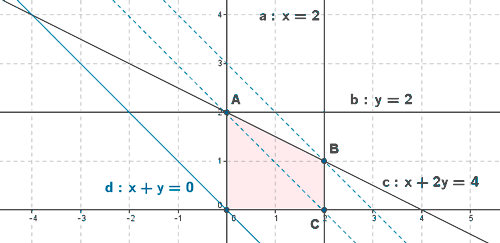
- Para x + y = 0, tenemos que b > 0. Como queremos maximizar la función bastará con tomar el vértice por el cual pasa la paralela a x + y = 0 con mayor ordenada en el origen. Dicho vértice es el vértice B. Por tanto la función alcanza su máximo en el vértice B.
- Calculamos el vértice elegido en el paso anterior.
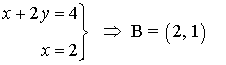
Como el vértice que maximiza la función es el vértice B, el rectángulo con mayor perímetro posible bajo las restricciones dadas es el que tiene lados 2 y 1.
15) Considera el triángulo de vértices (0,0), (2,8) y (10,3). Determina razonadamente:
a) El punto del triángulo donde la función F(x,y) = -4x + y + 9 alcanza el máximo.
b) El punto del triángulo donde la función G(x,y) = 4x + y + 9 alcanza el máximo.
a)
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
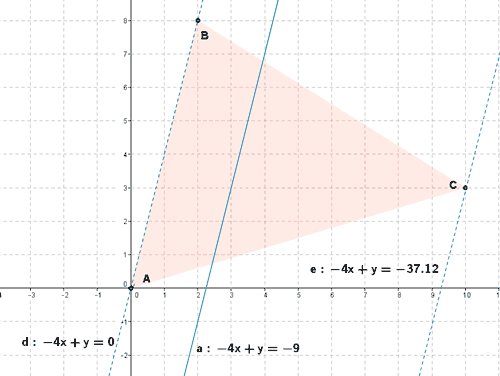
- No hace falta que calculemos los vértices ya que nos los da el enunciado del problema.
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo:
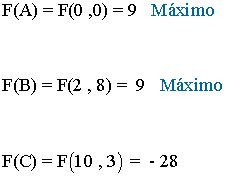
- Tanto el vértice A como el vértice B maximizan la función. Por tanto los puntos que harán máxima la función son todos los puntos del lado que une los vértices A y B.
Pensando en el método gráfico, esto puede apreciarse claramente ya que vemos que la paralela a
-4x + y = - 9 que pasa por alguno de los vértices del triángulo con ordenada máxima es -4x + y = 0, que pasa por los vértices A y B. Dicha recta también es la recta paralela a -4x + y = - 9 que pasa por todos los puntos del segmento A y B, de manera que por todos ellos pasa la recta paralela a
-4x + y = - 9 con ordenada máxima, lo cual nos asegura que dichos puntos también maximizan la función.
b)
Vamos a resolver el problema empleando el método analítico:
- Se representa gráficamente la región factible
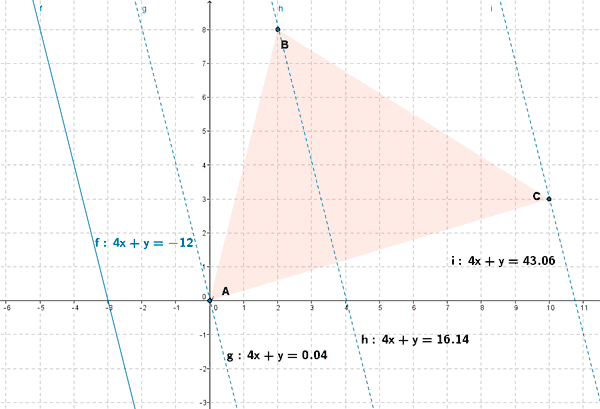
- No hace falta que calculemos los vértices ya que nos los da el enunciado del problema.
- Como el máximo se alcanza en uno de estos puntos, se evalúa la función objetivo en cada uno de ellos, para ver en cuál de ellos se obtiene dicho máximo:
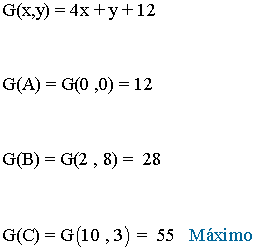
- La función alcanza su máximo en el punto C.


 INICIO
INICIO