Ejercicios resueltos de sistemas de inecuaciones lineales con dos incógnitas
Resuelve el siguiente sistema de inecuaciones:
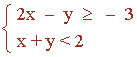
Conjunto de soluciones de la primera inecuación:
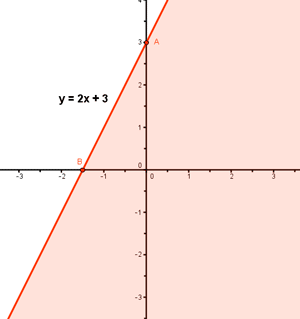
2x - y = - 3 ⇔ y = 2x + 3
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 2x + 3 = 3 ⇒ A = (0 , 3)
y = 0 ⇒ 0 = 2x + 3 ⇒ x = - 3/2 ⇒ B = (- 3/2 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , 2x - y ≥ - 3 ⇒ 0 ≥ - 3
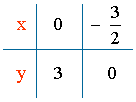
Conjunto de soluciones de la segunda inecuación:
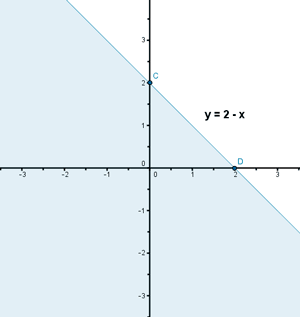
x + y = 2 y = 2 - x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 2 - x = 2 ⇒ C = (0 , 2)
y = 0 ⇒ 0 = 2 - x ⇒ x = 2 ⇒ D = (2 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0, 0) , x + y < 2 ⇒ 0 < 2
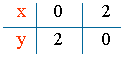
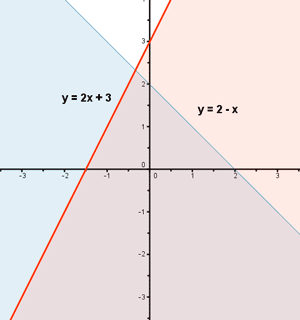
El conjunto de soluciones del sistema estará formado por aquellos valores de x que cumplan ambas inecuaciones, por tanto, la solución será la intersección de ambos semiplanos:
Resuelve el siguiente sistema de inecuaciones:
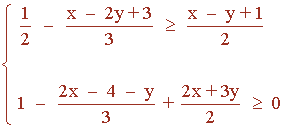
Aplicamos m.c.m.(2 , 3) = 6 en ambas inecuaciones:
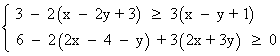
![]()
![]()
Conjunto de soluciones de la primera inecuación:
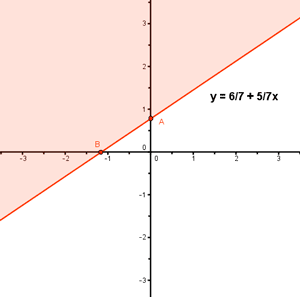
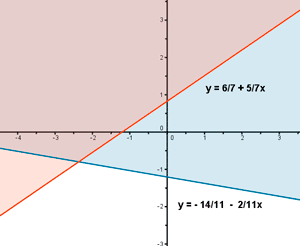
- 5x + 7y = 6 ⇔ 7y = 6 + 5x ⇔ y = 6/7 + 5/7x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 6/7 + 5/7x = 6/7 ⇒ A = (0 , 6/7)
y = 0 ⇒ 0 = 6/7 + 5/7x ⇒ x = - 6/5 ⇒ B = (-6/5 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , - 5x + 7y ≥ 6 ⇒ 0 ≥ 6 ¡no es cierto!
Probamos con otro punto del otro lado de la recta, por ejemplo:
(- 2 , 2) , - 5x + 7y ≥ 6 ⇒ 10 + 14 ≥ 6 24 ≥ 6
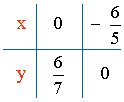
Conjunto de soluciones de la segunda inecuación:
2x + 11y = - 14 ⇔ 11y = - 14 - 2x ⇔ y = - (14/11) - (2/11)x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = - 14/11 ⇒ C = (0 , - 14/11)
y = 0 ⇒ 0 = - (14/11) - (2/11)x ⇒ x = - 7 ⇒ D = ( - 7 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , 2x + 11y ≥ - 14 ⇒ 0 ≥ - 14
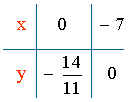
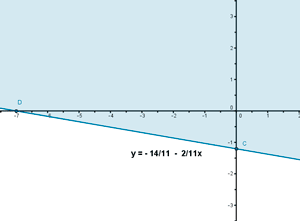
El conjunto de soluciones del sistema estará formado por aquellos valores de x que cumplan ambas inecuaciones, por tanto, la solución será la intersección de ambos semiplanos:
Resuelve el siguiente sistema de inecuaciones:
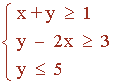
Conjunto de soluciones de la primera inecuación:
x + y = 1 ⇔ y = 1 - x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 1 - x = 1 ⇒ A = (0 , 1)
y = 0 ⇒ 0 = 1 - x ⇒ x = 1 ⇒ B = (1 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , x + y ≥ 1 ⇒ 0 ≥ 1 ¡no es cierto!
Probamos con otro punto del otro lado de la recta, por ejemplo:
(2 , 2) , x + y ≥ 1 ⇒ 4 ≥ 1
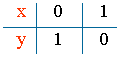
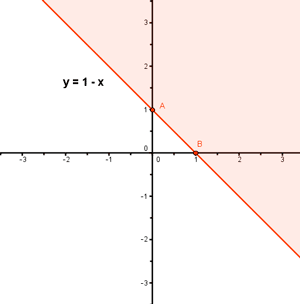
Conjunto de soluciones de la primera inecuación:
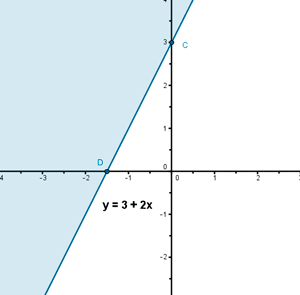
y - 2x = 3 ⇔ y = 3 + 2x
Puntos de corte de la recta con los ejes:
x = 0 ⇒ y = 3 + 2x = 3 ⇒ C = (0 , 3)
y = 0 ⇒ 0 = 3 + 2x ⇒ x = - 3/2 ⇒ D = (- 3/2 , 0)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , y - 2x ≥ 3 ⇒ 0 ≥ 3 ¡no es cierto!
Probamos con otro punto, por ejemplo:
(- 2 , 2) , y - 2x ≥ 3 ⇒ 6 ≥ 3
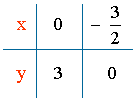
Conjunto de soluciones de la primera inecuación:
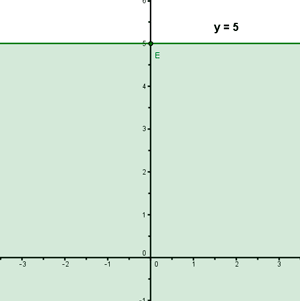
y = 5
La recta sólo corta al eje de abcisas: para cualquier valor de x siempre se tiene y = 5.
Por ejemplo, si x = 0 ⇒ (0 , 5)
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:
(0 , 0) , y ≤ 5 ⇒ 0 ≤ 5
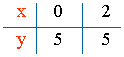
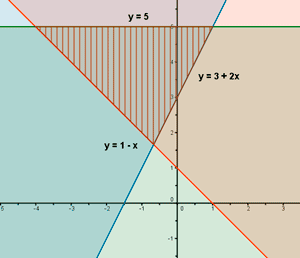
El conjunto de soluciones del sistema estará formado por aquellos valores de x que cumplan las tres inecuaciones, por tanto, la solución será la intersección de los tres semiplanos:


 INICIO
INICIO