Ejercicios resueltos de inecuaciones con dos incógnitas

Resuelve la siguiente inecuación:

y ≥ 4

Ecuación asociada:     y = 4

Para cualquier valor de  x  tenemos  y = 4.

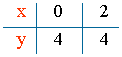
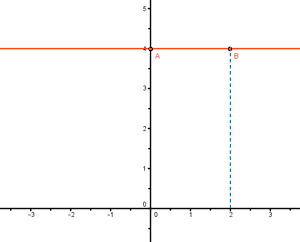
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:

(0 , 0)     ,     y ≥ 4     ⇒     0 ≥ 4    ¡no es cierto!

(0 , 5)     ,     y ≥ 4     ⇒     5 ≥ 4

Además, incluimos la recta dentro del conjunto solución, ya que la inecuación requiere que sea mayor o igual que 4.

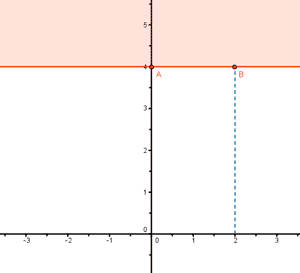
La solución de la inecuación es el semiplano que queda por encima de la recta y = 4, incluida ésta.

Resuelve la siguiente inecuación:

x ≤ - 3

Ecuación asociada:     x = - 3

Para cualquier valor de  y  tenemos  x = - 3.

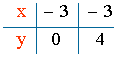
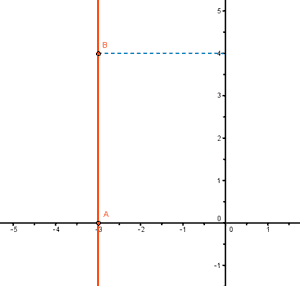
Probamos con puntos a ambos lados de la recta para ver cuál cumple la inecuación:

(0 , 0)     ,     x ≤ - 3     ⇒     0 ≤ - 3     ¡no es cierto!

(- 4 , 0)     ,     x ≤ - 3     ⇒     - 4 ≤ - 3

Además, incluimos la recta dentro del conjunto solución, ya que la inecuación requiere que sea menor o igual que - 3.

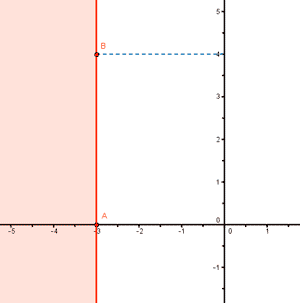
La solución de la inecuación es el semiplano que queda a la izquierda de la recta x = - 3, incluida ésta.

Resuelve la siguiente inecuación:

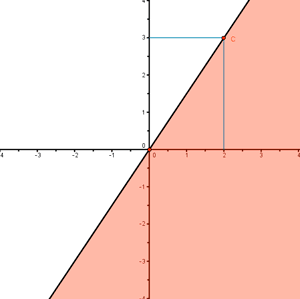
3x - 2y > 0

      1.   Representamos gráficamente la ecuación lineal asociada a la inecuación, es decir:   3x - 2y = 0

                  3x - 2y = 0   ⇒   3x = 2y   ⇒   y = 3x/2

      Para ello, calculamos los puntos de corte con los ejes:

      Si x = 0   ⇒  

    

 ⇒   tenemos el punto de la recta:  (0 , 0)

      Si y = 0 tenemos que x = 0, y obtenemos el mismo punto: (0 , 0). Así que vamos a calcular otro punto, por ejemplo para x = 2.

      Si x = 2   ⇒  

 

  

 ⇒   tenemos el punto de la recta:  C = (2 , 3)

      

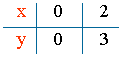
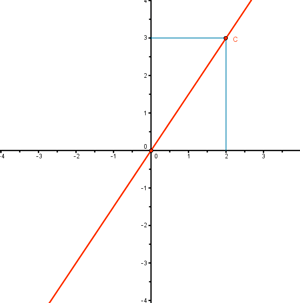
      Observamos que la recta divide al plano en dos semiplanos.

      2.  Discutimos cuál de los semiplanos es solución utilizando un punto a cada lado de la recta y estudiando si verifica o no la inecuación.

                  Vamos a comprobar el punto:  (- 1, 1)

                  3x - 2y > 0   ⇒   3·(-1) - 2·1 = - 5 < 0

      Como el punto (-1 , 1) no verifica la inecuación, el semiplano de la izquierda no es solución.

                  Vamos a comprobar el punto:  (1, 0)

                  3x - 2y > 0   ⇒   3·1 - 2·0 = 3 > 0

      Como el punto (1 , 0) verifica la inecuación, la solución de la inecuación es el semiplano de la derecha.

      3.  Inclusión o no de la recta o frontera en la solución:

      En este caso, no se incluye la recta, ya que sólo es > y no =.

Resuelve la siguiente inecuación:

y ≥ x² - 1

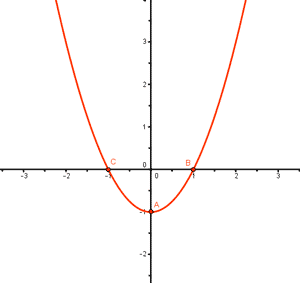
Ecuación asociada:     y = x² - 1

Calculamos los puntos de corte con los ejes:

Si  x = 0     ⇒     y = x² - 1 = - 1     A = (0 , - 1)

Si  y = 0     ⇒     0 = x² - 1     ⇒     x² = 1     ⇒     x = ± 1     B = (1 ,0)  ,  C = (- 1 , 0)

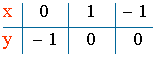
Probamos con puntos a ambos lados de la parábola para ver cuál cumple la inecuación:

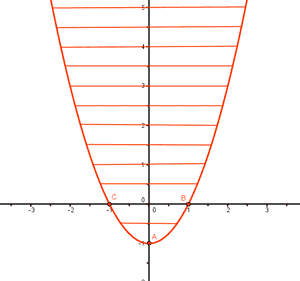
(0 , 0)     ,     y ≥ x² - 1     ⇒     0 ≥ - 1

Además, incluimos la parábola dentro del conjunto solución, ya que la inecuación requiere que sea mayor o igual.