Ecuaciones y sistemas matriciales
Ecuaciones o sistemas matriciales son aquellas ecuaciones o sistemas en los que las incógnitas o coeficientes son matrices.
Resumen de ecuaciones matriciales básicas
| Ecuación | Pasos | Solución |
|---|---|---|
| X·A = B | Multiplicamos por la derecha por A-1 | X·A·A-1 = B·A-1 ⇒ X = B · A-1 |
| A·X + B = C | Restamos B en ambos miembros Multiplicamos por la izquierda por A-1 |
A·X + B - B = C - B ⇒ A·X = C - B A-1·A·X = A-1·(C - B) ⇒ X = A-1 · (C - B) |
| X·A + B = 3 C | Restamos B en ambos miembros Multiplicamos por la derecha por A-1 > |
X·A + B - B = 3 C - B ⇒ X·A = 3 C - B X·A·A-1 = ( 3 C - B)·A-1 ⇒ X = (3C - B) · A-1 |
| A·X + B·X = 5C | Sacamos X factor común. Multiplicamos por la izquierda por (A + B)-1 |
(A +B )·X = 5C (A + B)-1(A +B )·X = 5(A + B)-1C ⇒ X = 5(A + B)-1·C |
| X·C - X·A·B = 3C | Sacamos X factor común. Multiplicamos por la derecha por (C + A · B )-1 |
X·(C + A·B) = 3C X·(C + A·B )(C + A·B )-1 = 3C(C + A·B )-1 ⇒ X = 3C·(C + A · B )-1 |
Comprobar las siguientes ecuaciones matriciales:
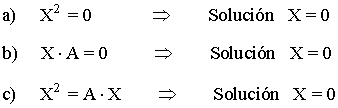
a) No es correcta, porque hay matrices no nulas que multiplicadas por si mismas dan la matriz cero. Por ejemplo:
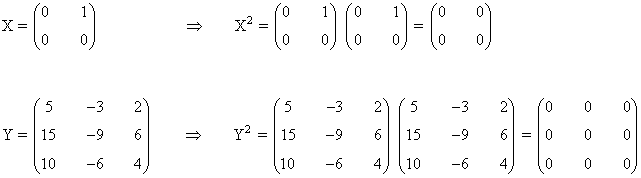
b) Si la matriz A tiene inversa la única solución es X = 0 . En cambio, si no existe A-1 pueden haber otras soluciones como en el caso anterior.
c) Si reescribimos la ecuación de la siguiente forma: X2 - AX = 0 ⇒ X(X - A) = 0
Se ve que pueden haber otras soluciones, puesto es un caso particular del apartado anterior.
Ejemplos de ecuaciones matriciales
1) Dadas las matrices
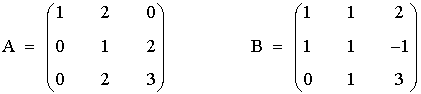
- Determinar la matriz inversa de B
- Determinar una matriz X tal que A = B · X
Empezamos determinando la matriz inversa de B

Dado que B es una matriz inversible, para encontrar una matriz X tal que se satisfaga la ecuación
A = B · X
bastará con multiplicar por B-1 por la izquierda ambos miembros de la ecuación. De esta forma obtenemos que B-1 · A = B-1 · B · X = X, es decir
X= B-1 · A
Calculemos ahora la matriz X:
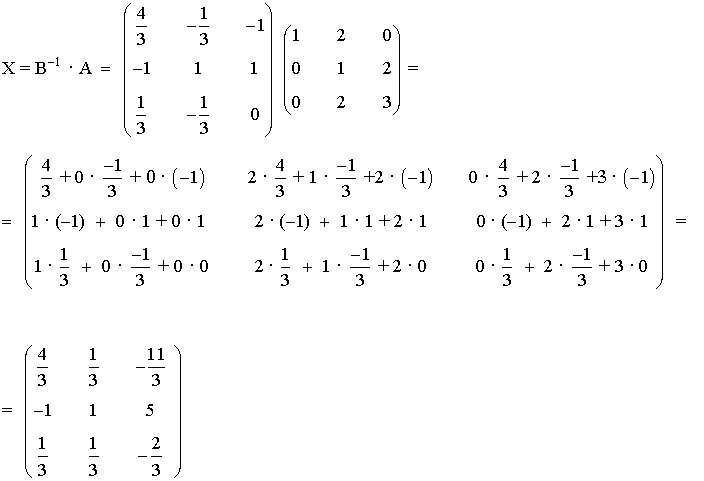
2) Resolver la ecuación matricial A · X = B donde
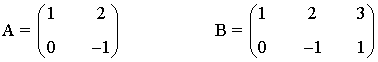
Si A es inversible, entonces para resolver la ecuación basta con multiplicar ambos miembros de la igualdad por la izquierda por A-1, de manera que obtenemos que
X = A-1 · B
Empezamos intentando calcular la inversa de A:
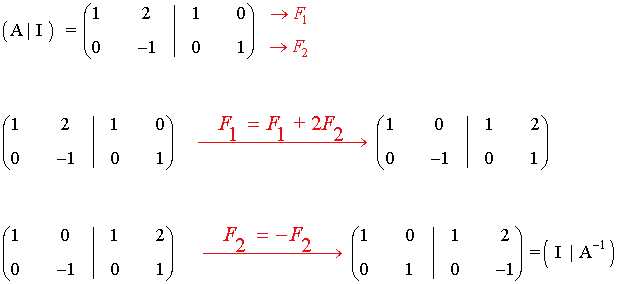
Como A es inversible,
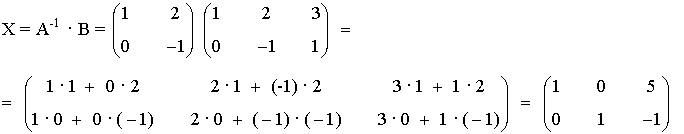
3) Siendo A y B dos matrices de orden 2, resolver el siguiente sistema matricial
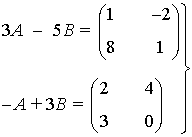
Solución:
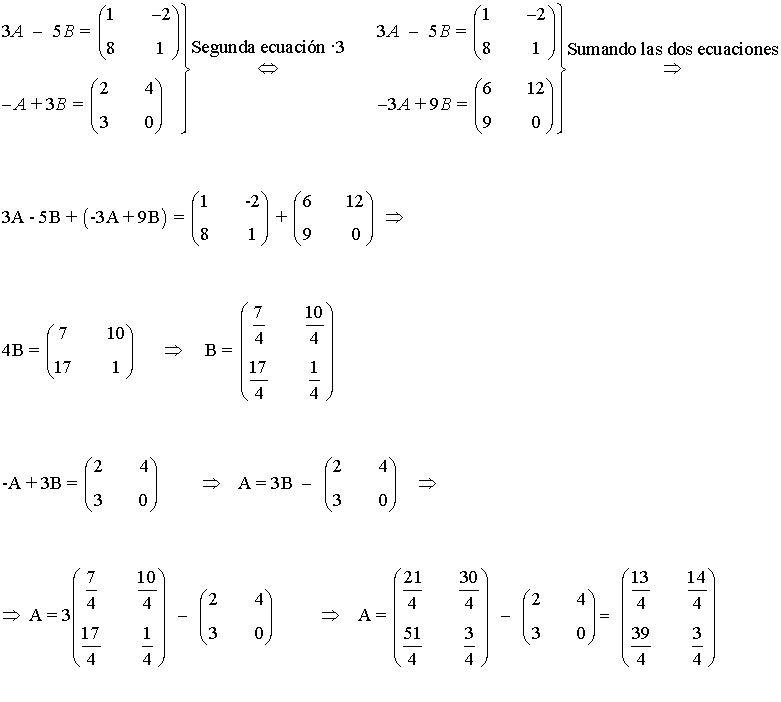


 INICIO
INICIO

