Ejercicios resueltos de rango de una matriz por el método de Gauss
Método de Gauss
- Cambiar el orden de las filas: Fi ↔ Fj
- Multiplicar una o más filas por un número real distinto de cero: Fi → k Fj
- Sumar a una fila otra multiplicada por un número real: Fi → Fi + k Fj
1) Hallar el rango de la matriz A utilizando el método de Gauss:
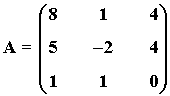
2) Hallar el rango de la matriz B utilizando el método de Gauss:
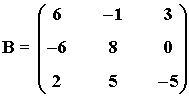
3) Hallar el rango de la matriz B utilizando el método de Gauss:
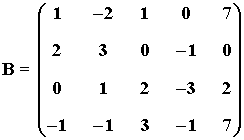
4) Hallar el rango de la matriz B utilizando el método de Gauss:
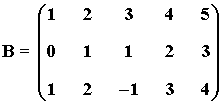
5) Discutir, según el valor de m , el rango de la matriz:
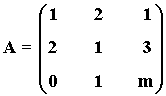
6) Obtener el valor de m para que el rango de la matriz A sea igual a 2:
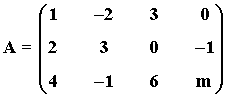
7) Haz uso del método de Jordan y discute el rango de la matriz A según los valores del parámetro m :
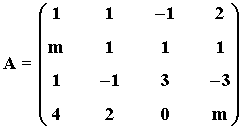
8) Dada la siguiente matriz:
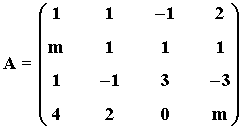
a) Determinar los valores de m para que rango(A) < 3
b) ¿Puede ser rango (A) = 1 para algún valor de m ?
1) Hallar el rango de la matriz A utilizando el método de Gauss:
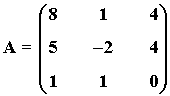
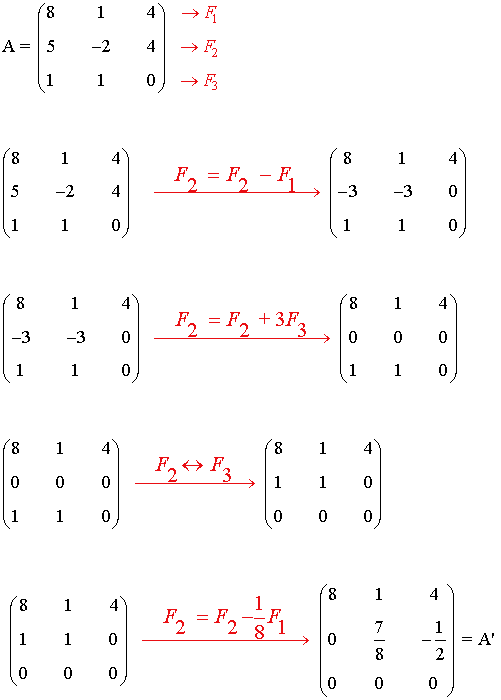
La matriz A' es una matriz escalonada equivalente a A y tiene 2 filas no nulas.
Por tanto rg(A) = 2 .
2) Hallar el rango de la matriz B utilizando el método de Gauss:
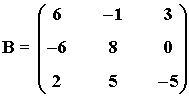
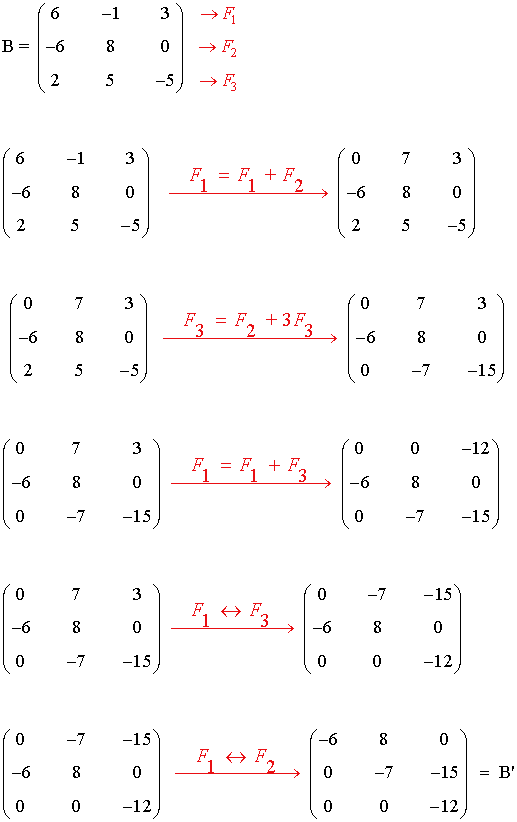
La matriz B' es una matriz escalonada equivalente a B y tiene 3 filas no nulas.
Por tanto rg(B) = 3 .
3) Hallar el rango de la matriz B utilizando el método de Gauss:
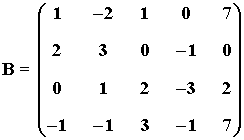

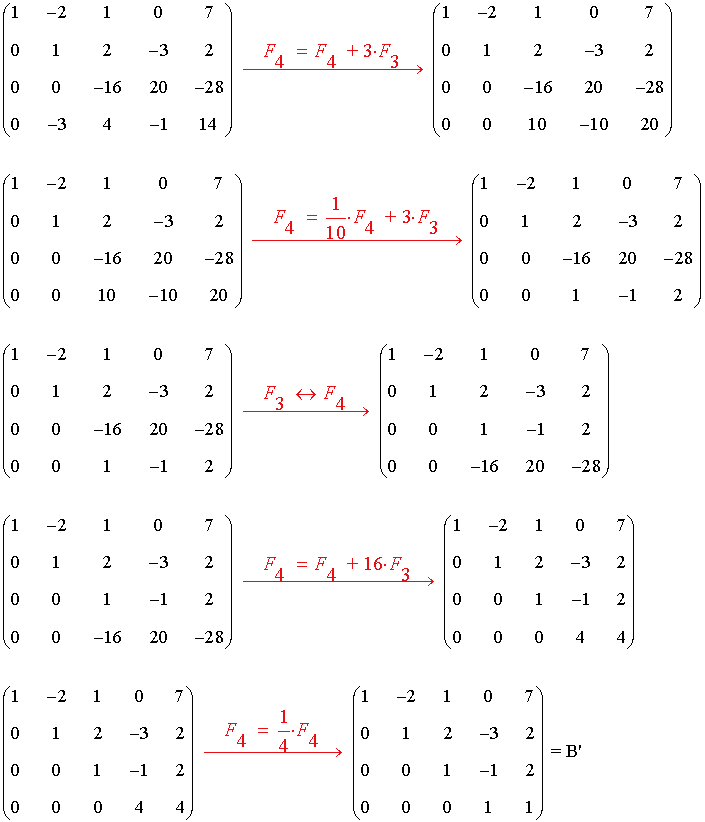
La matriz B' es una matriz escalonada equivalente a B y tiene 4 filas no nulas.
Por tanto rg(B) = 4 .
4) Hallar el rango de la matriz B utilizando el método de Gauss:
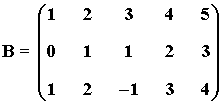
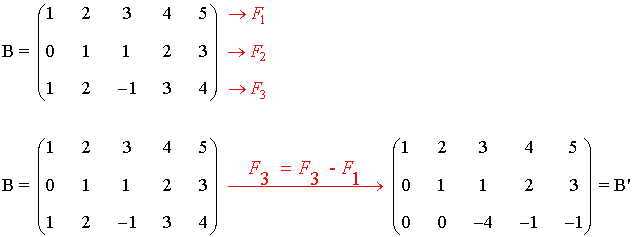
La matriz B' es una matriz escalonada equivalente a B y tiene 3 filas no nulas.
Por tanto rg(B) = 3 .
5) Discutir, según el valor de m , el rango de la matriz:
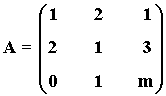
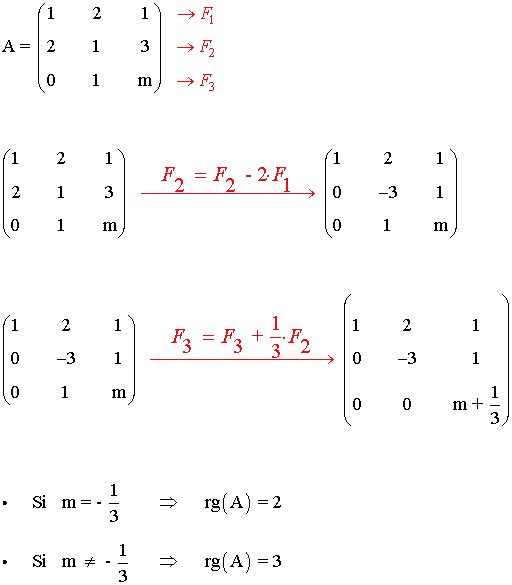
6) Obtener el valor de m para que el rango de la matriz A sea igual a 2:
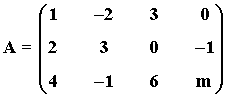
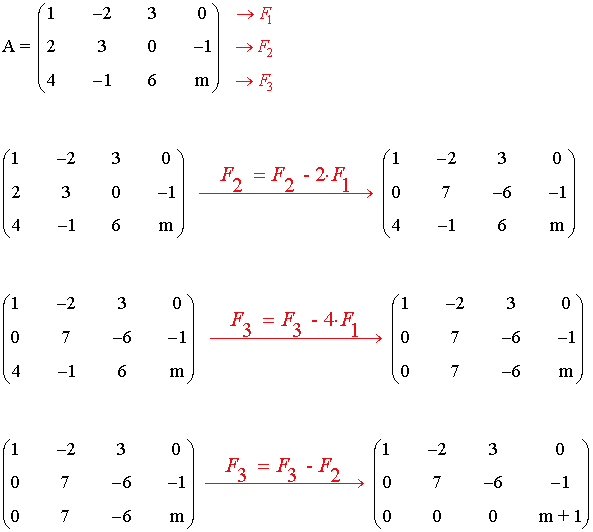
Para que el rango sea 2, la última fila tiene que ser nula, es decir:
m + 1 = 0 ⇒ m = - 1
7) Haz uso del método de Jordan y discute el rango de la matriz A según los valores del parámetro m :
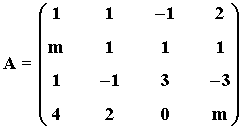
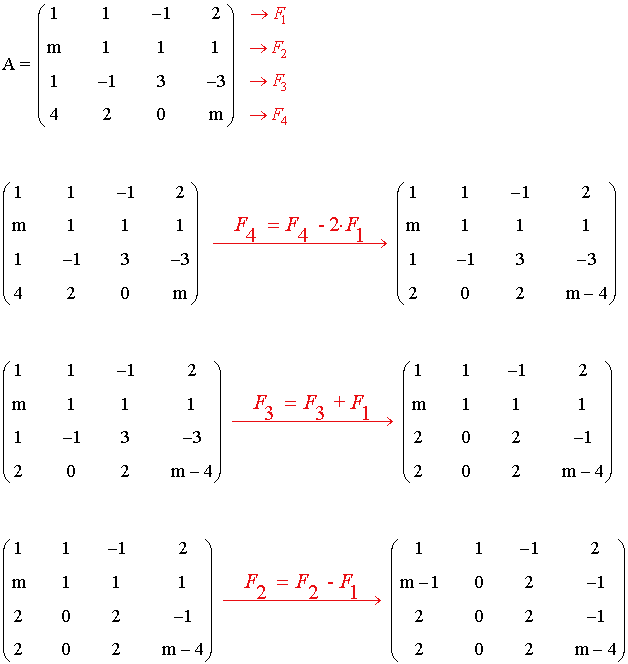
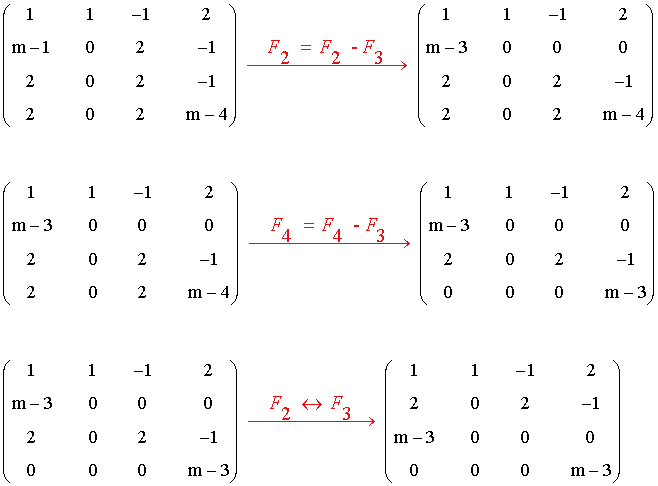
Intercambiando las columnas obtenemos la siguiente matriz escalonada:
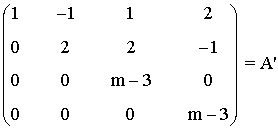
• Si m = 3 ⇒ rg(A) = 2 (dos filas no nulas)
• Si m ≠ 3 ⇒ rg(A) = 4 (cuatro filas no nulas)
8) Dada la siguiente matriz:
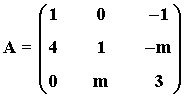
a) Determinar los valores de m para que rango(A) < 3
b) ¿Puede ser rango (A) = 1 para algún valor de m ?
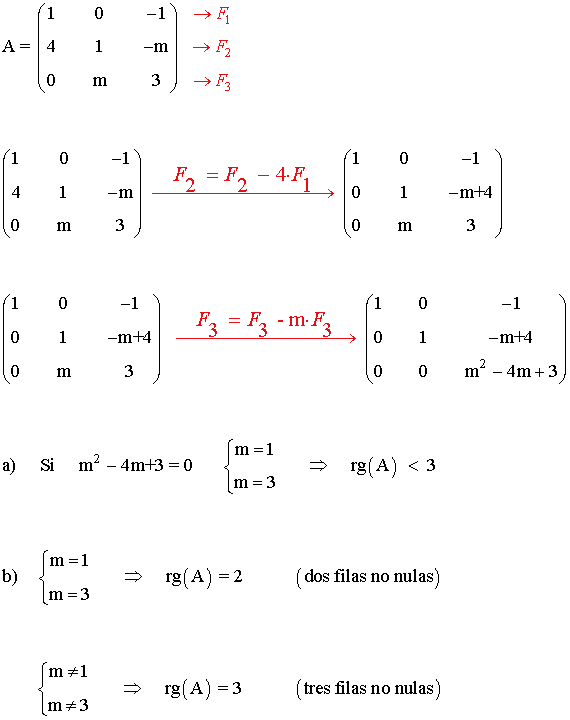
Es decir, el rango de la matriz A no puede ser 1 para ningún valor de m .


 INICIO
INICIO