Ejercicios resueltos de rango de una matriz
(dependencia lineal de filas o columnas)
1) Obtener razonadamente el rango de la matriz A :
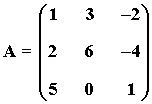
2) Comprobar que en la matriz B el número de filas linealmente independientes coincide con el número de columnas linealmente independientes:
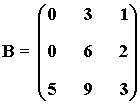
3) Completa los elementos para que la primera y la segunda fila sean linealmente dependientes:
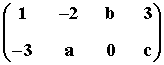
4) Determina el rango de las siguientes matrices:
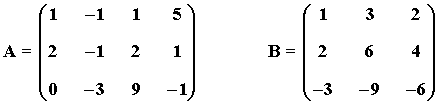
5) ¿Cuál es el mayor número de columnas linealmente independientes de la siguiente matriz?
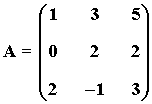
6) Dadas las matrices:
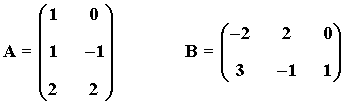
¿Es cierto que rg(A·B) = rg(A)·rg(B) ? Justifica tu respuesta.
7) Halla el rango de la matriz A:
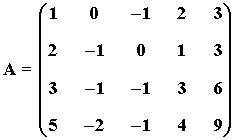
8) Halla el rango de la matriz:
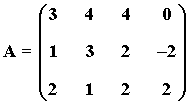
1) Obtener razonadamente el rango de la matriz A :
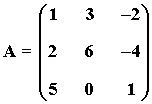
La fila segunda es el doble de la primera fila. Por otra parte, la fila primera y segunda no son proporcionales.
Por lo tanto rg(A) = 2
2) Comprobar que en la matriz B el número de filas linealmente independientes coincide con el número de columnas linealmente independientes:
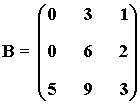
Por filas:
• La fila segunda es el doble de la fila primera.
• La fila primera y la fila tercera no son proporcionales ⇒ rg(B) = 2
Por columnas:
• La columna segunda es el triple de la columna tercera.
• La columna primera y la columna segunda no son proporcionales ⇒ rg(B) = 2
3) Completa los elementos para que la primera y la segunda fila sean linealmente dependientes:
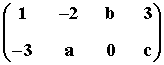
Para que las dos filas sean linealmente dependientes se tiene que dar que F1 = λ·F2
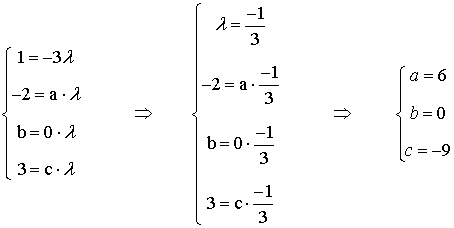
4) Determina el rango de las siguientes matrices:
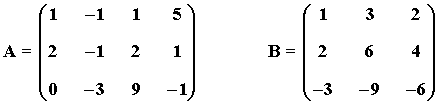
a) Para que alguna filia sea linealmente dependiente de otras se tiene que dar F1 = λ·F2 + µ·F3
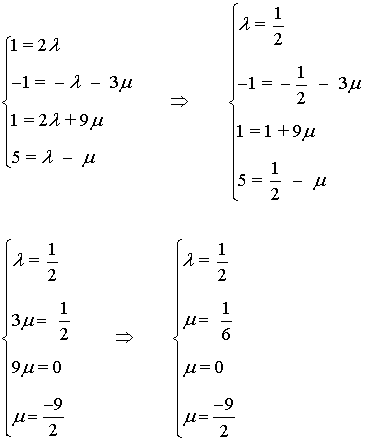
Como los valores de µ son diferentes, entonces las tres filas son linealmente independientes ⇒ rg(A)=3
b) En este caso se cumple que F2 = 2·F1 y F3 = (-3)·F1
Por lo tanto rg(A)=1
5) ¿Cuál es el mayor número de columnas linealmente independientes de la siguiente matriz?
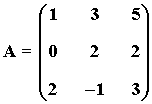
La tercera columna es combinación lineal de ella misma con las columnas primera y segunda:
Es decir, se cumple que: C3 = C3 - 2·C1 - C2
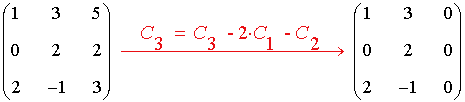
Como hay una columna nula, el rango por columnas es 2, es decir, solo hay dos columnas linealmente independientes.
6) Dadas las matrices:
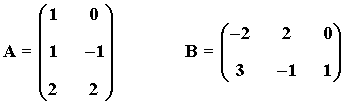
¿Es cierto que rg(A·B) = rg(A)·rg(B) ? Justifica tu respuesta.
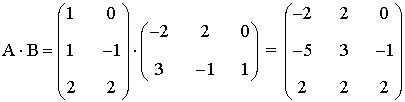
Estudiando por separado los rangos de A·B , A y B obtenemos que:
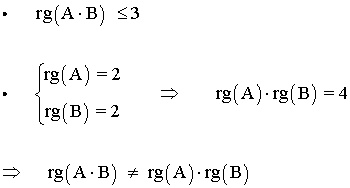
Es decir, el rango del producto de las matrices A y B es distinto que el producto de los rangos de las matrices.
7) Halla el rango de la matriz A:
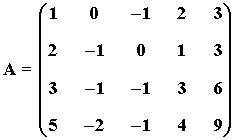
La fila tercera es la suma de la primera y la segunda.
La fila cuarta es la suma de la segunda y la tercera.
Las filas primera y segunda no son proporcionales ⇒ rg(A) = 2
8) Halla el rango de la matriz:
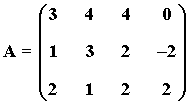
Como la primera fila es la suma de las filas segunda y tercera, podemos eliminarla:
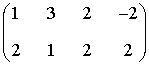
Estas dos filas no son proporcionales, por lo tanto, el rango de la matriz es 2.


 INICIO
INICIO