Ejercicios resueltos de cálculo de matriz inversa
por definición y por el método de Gauss-Jordan
Método de Gauss
- Cambiar el orden de las filas.
- Multiplicar una o más filas por un número real distinto de cero.
- Sumar a una fila otra multiplicada por un número real.
1) Calcular la matriz inversa de:
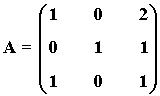
por el método de Gauss-Jordan
2) Halla la inversa de las siguientes matrices aplicando la definición:
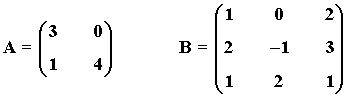
3) Halla, por el método de Gauss-Jordan, la matriz inversa de A:
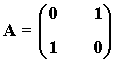
4) Dada la matriz A:
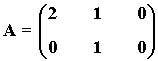
a) Razona si puede existir una matriz B tal que AB = I, siendo I la matriz identidad. En caso afirmativo halla B.
b) ¿Tiene inversa A? Razona la respuesta.
5) Calcular la matriz inversa de:
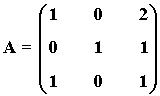
por el método de Gauss-Jordan
6) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
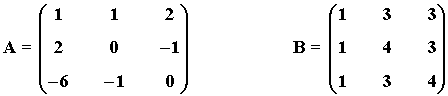
7) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
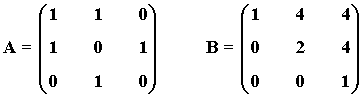
8) Comprueba que la inversa de la siguiente matriz:
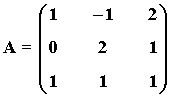
es la matriz:
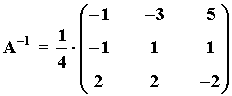
9) Dadas las matrices:
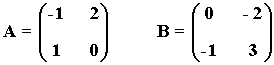
Calcula (A-1)-1 y (B-1)·B
10) Sean las matrices
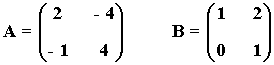
a) Comprueba que (A·B)-1= B-1·A-1
b) Calcula (B2)-1 , de la manera más rápida posible
11) Dada la matriz
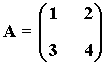
Calcula (At·A-1)2·A
12) Considera la matriz:
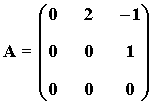
Prueba que B = I + A + A2 es la matriz inversa de I - A , donde I es la matriz identidad de orden 3.
13) Considera la matriz:
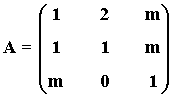
donde m∈IR . Determina para qué valores de m la matriz A es regular (inversible).
14) Consideremos la matriz A:
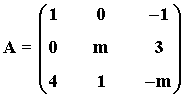
a) Averigua para que valores del parámetro m la matriz no tiene inversa
b) Calcula, si es posible, la matriz inversa de A para m = 2
15) Se consideran las matrices:
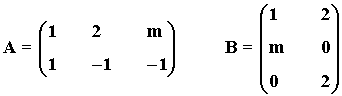
donde m es un número real. Encuentra los valores de m para los que A·B tiene inversa.
16) Se consideran las matrices:
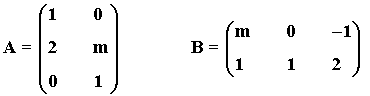
a) Estudia, en función de los valores reales de m , si la matriz B·A tiene inversa
b) Haz lo mismo para la matriz A·B
1) Hallar la inversa de A aplicando la definición:
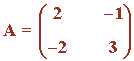
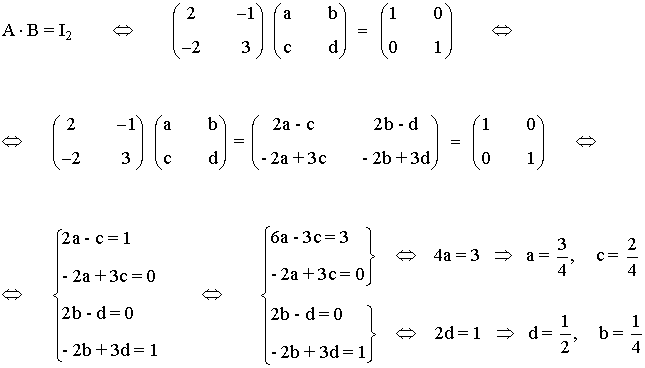
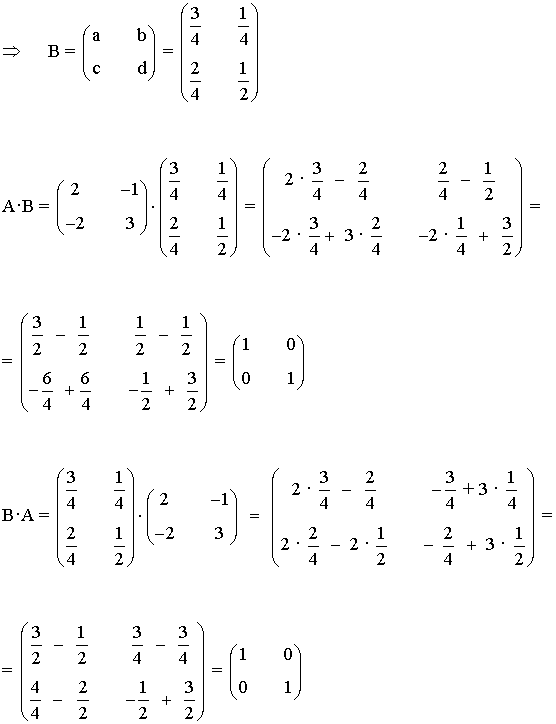
2) Halla la inversa de las siguientes matrices aplicando la definición:
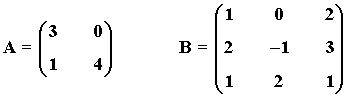
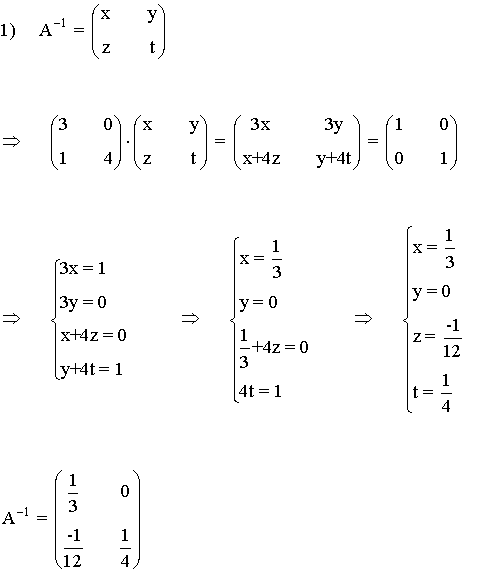
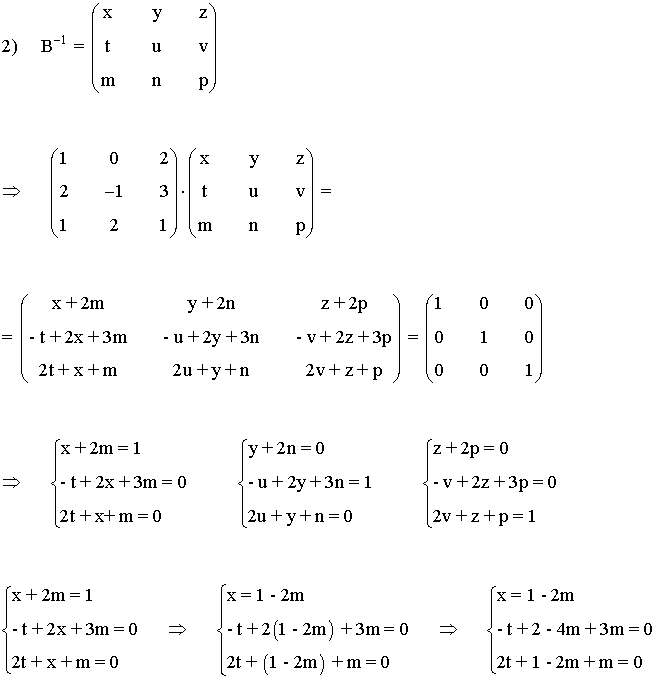
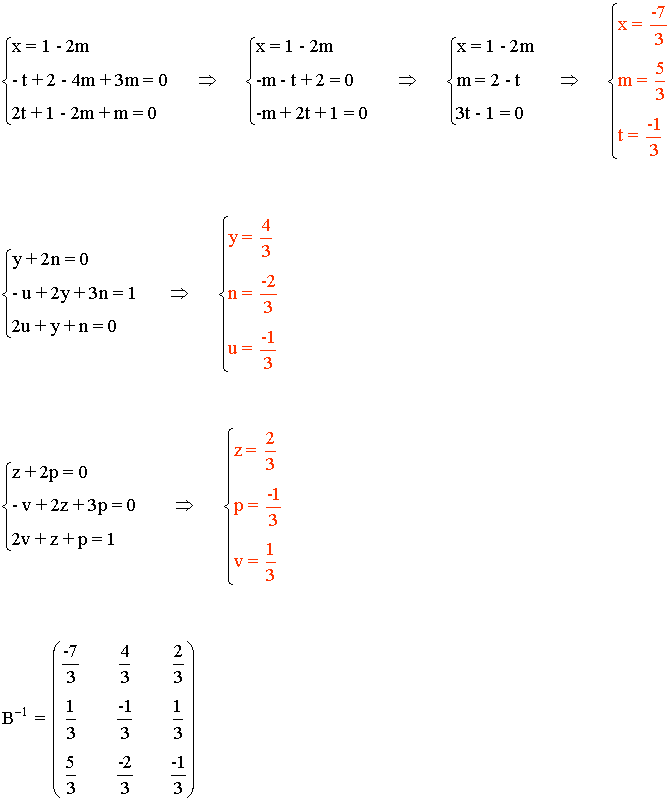
3) Halla, por el método de Gauss-Jordan, la matriz inversa de A:
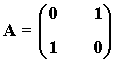
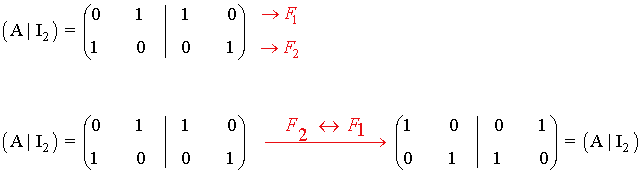
4) Dada la matriz A:
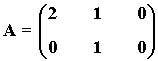
a) Razona si puede existir una matriz B tal que AB = I, siendo I la matriz identidad. En caso afirmativo halla B.
b) ¿Tiene inversa A? Razona la respuesta.
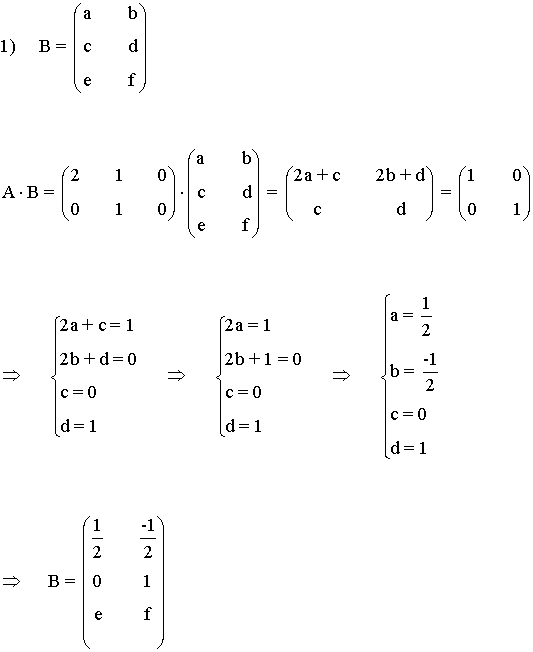
![]()
5) Calcular la matriz inversa de:
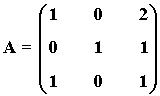
por el método de Gauss-Jordan
de manera que existe A-1 siendo:
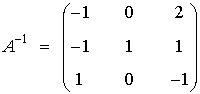
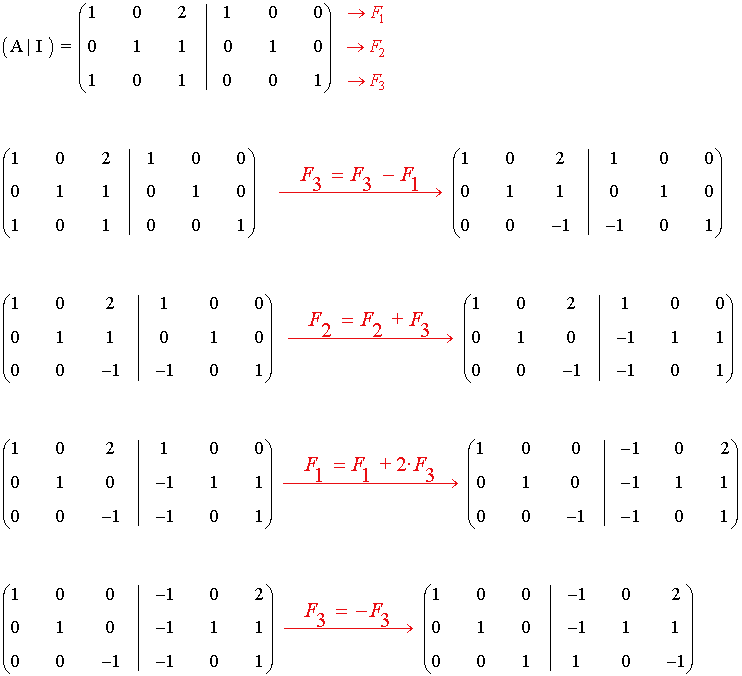
6) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
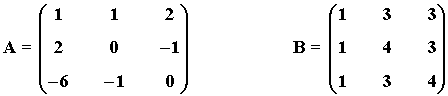
Empezamos calculando la inversa de la matriz A.
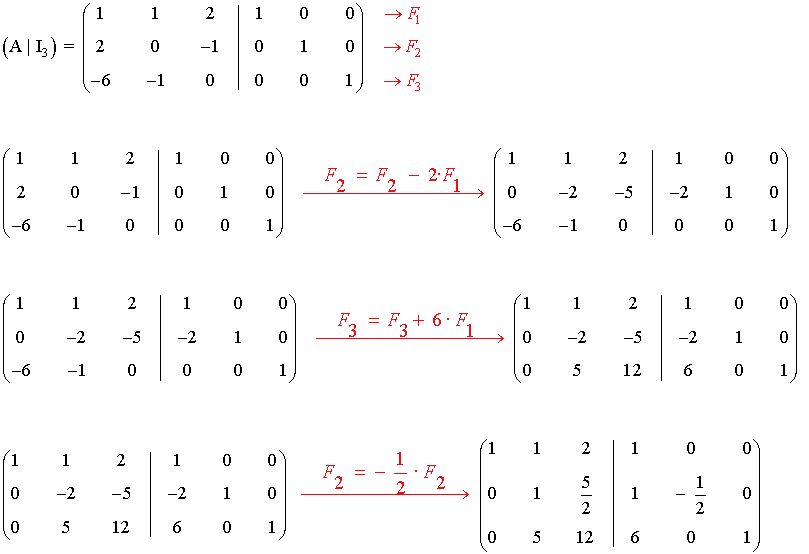
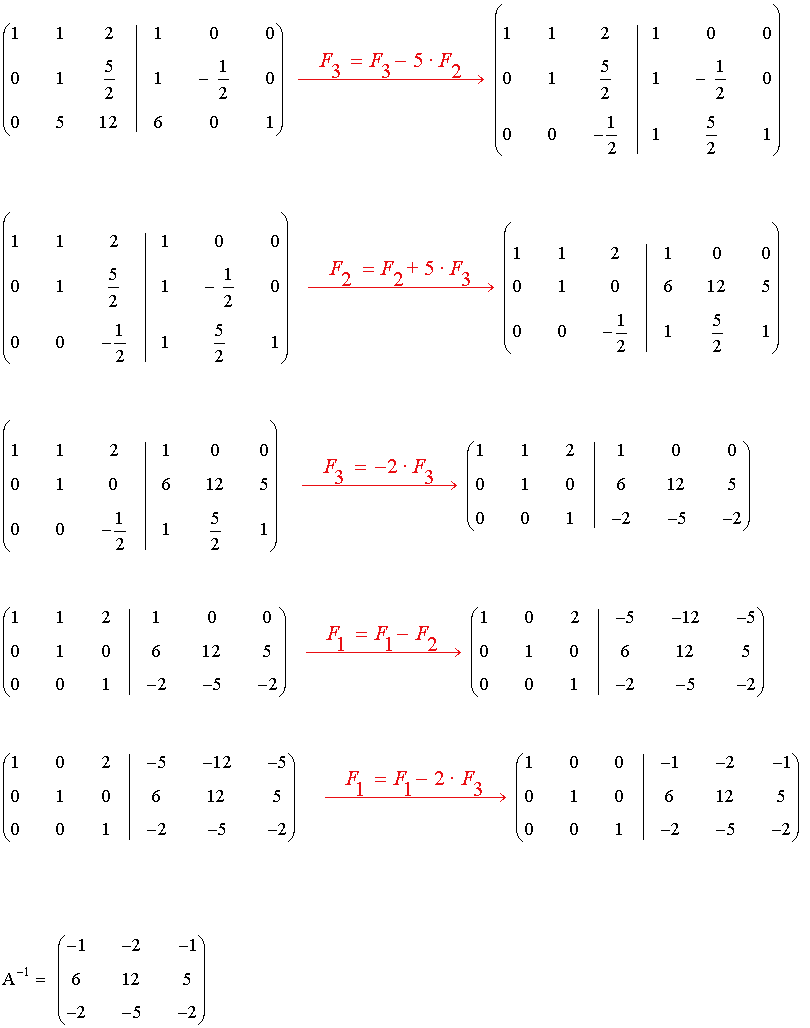
Calculamos ahora la inversa de B
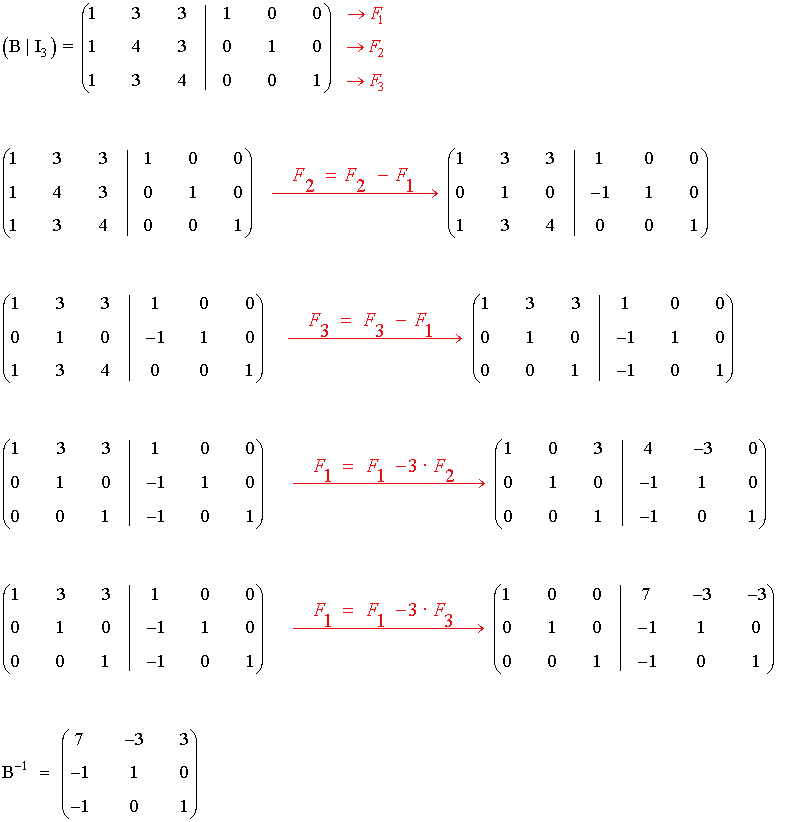
7) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
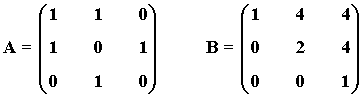
Empezamos calculando la inversa de la matriz A.
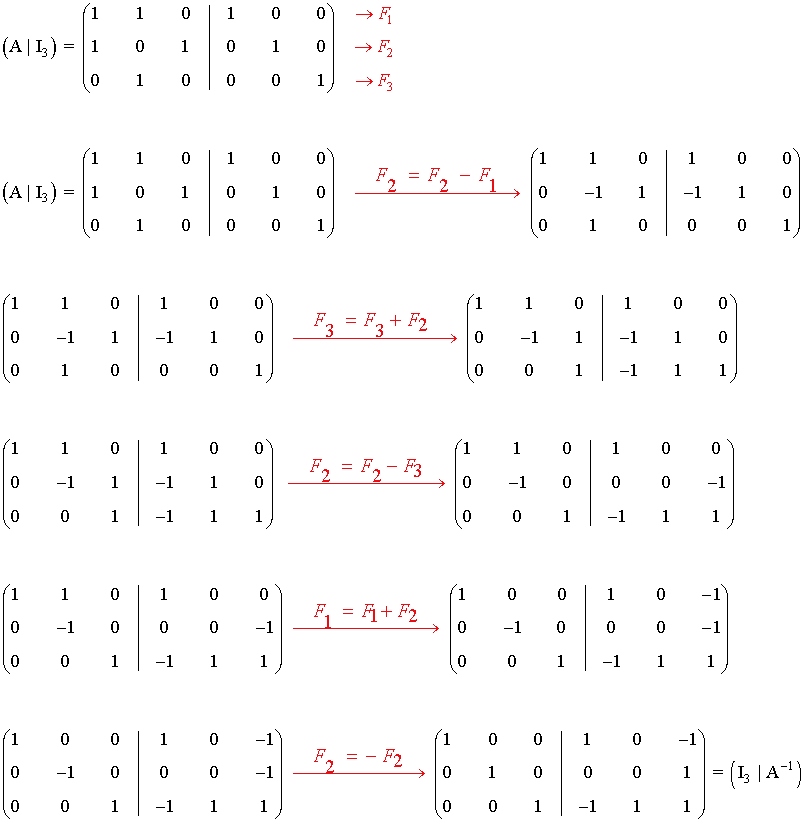
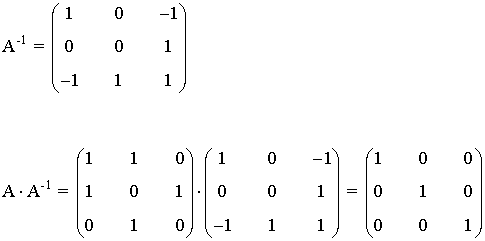
Calculamos ahora la inversa de B
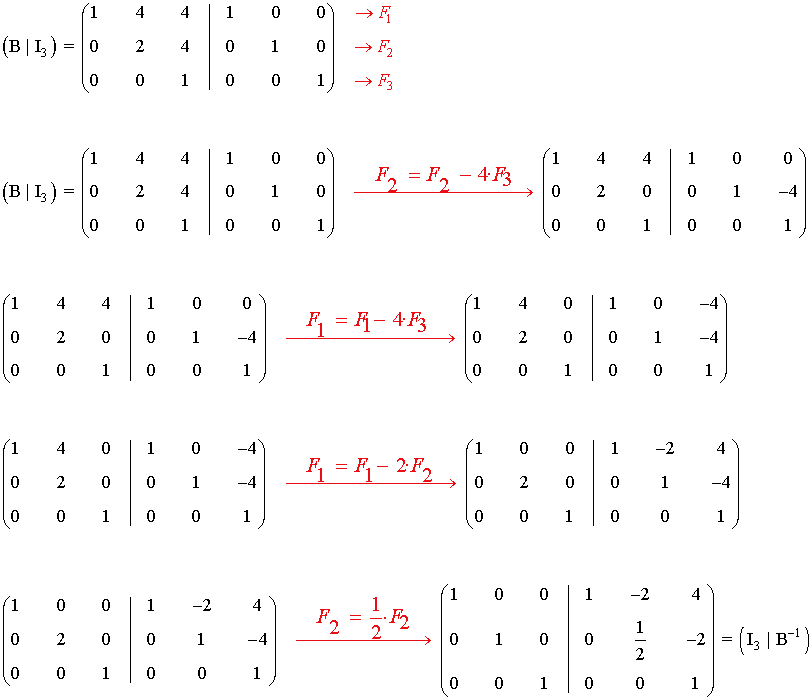
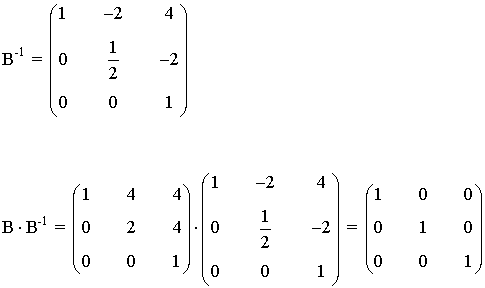
8) Comprueba que la inversa de la siguiente matriz
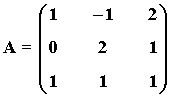
es la matriz:
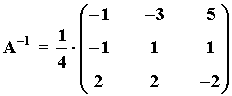
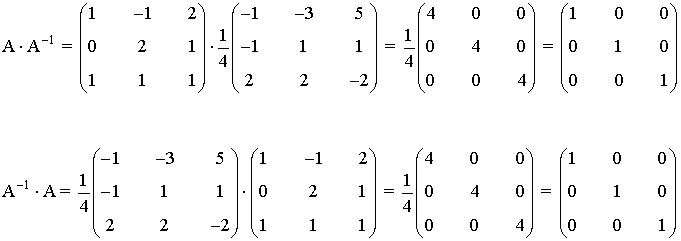
9) Dadas las matrices:
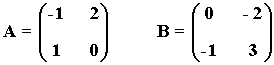
Calcula (A-1)-1 y (B-1)·B
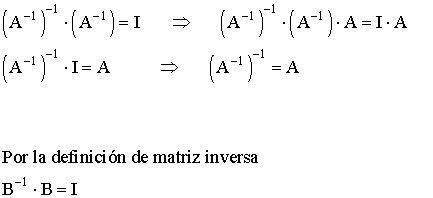
10) Sean las matrices
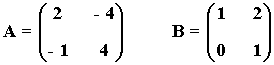
a) Comprueba que (A·B)-1= B-1·A-1
b) Calcula (B2)-1 , de la manera más rápida posible
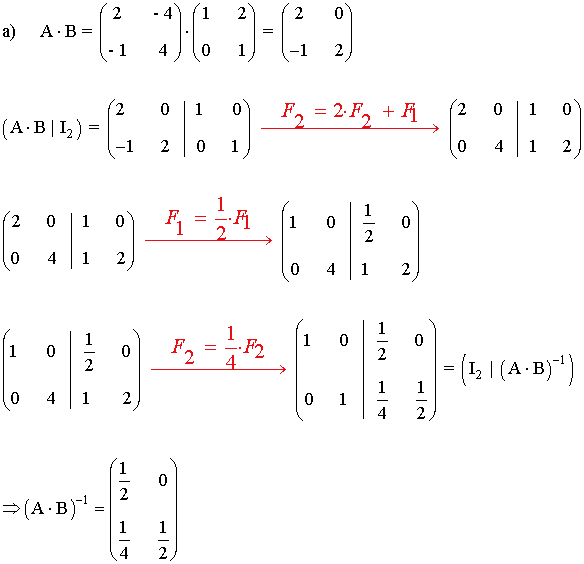
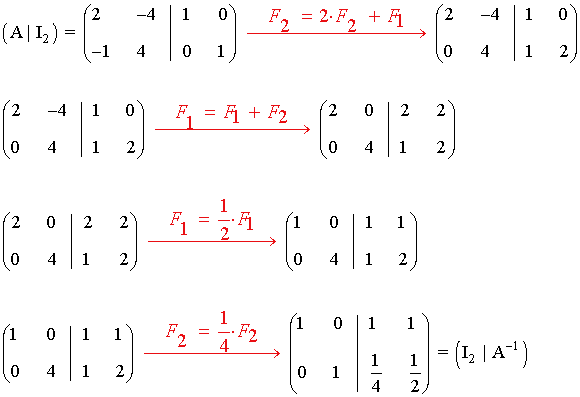
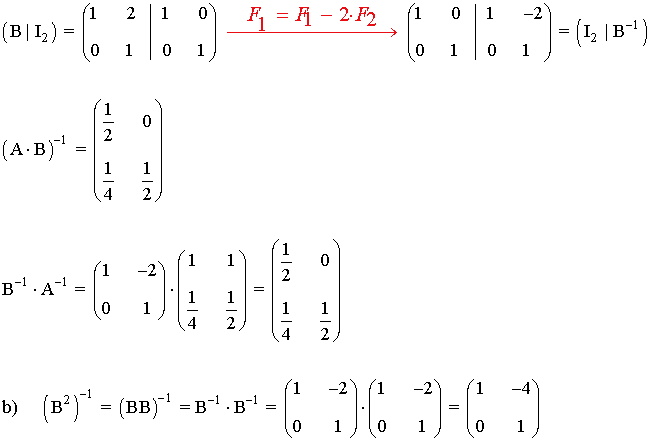
11) Dada la matriz
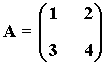
Calcula (At·A-1)2·A
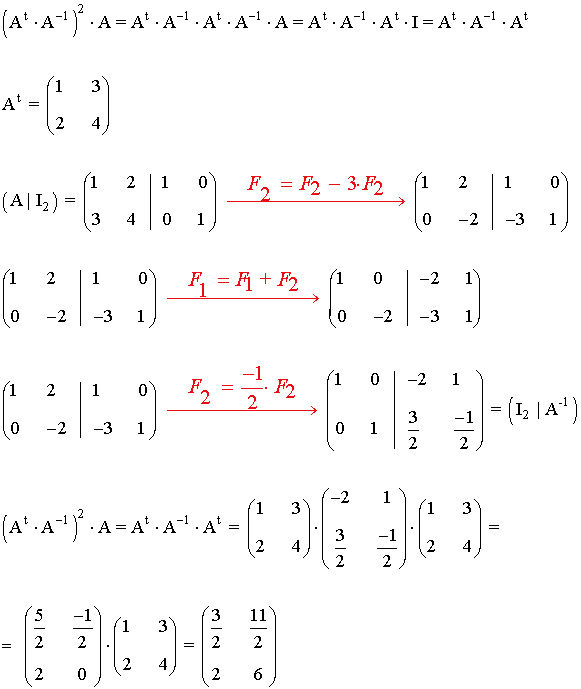
12) Considera la matriz:
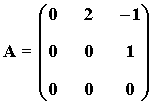
Prueba que B = I + A + A2 es la matriz inversa de I - A , donde I es la matriz identidad de orden 3
Si B es la matriz inversa de (I - A) entonces:
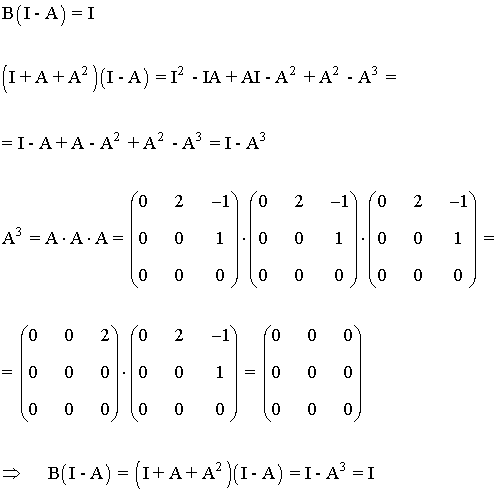
Es decir, B es la matriz inversa de (I - A)
13) Considera la matriz:
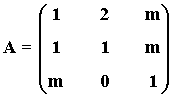
donde m∈IR . Determina para qué valores de m la matriz A es regular (inversible)
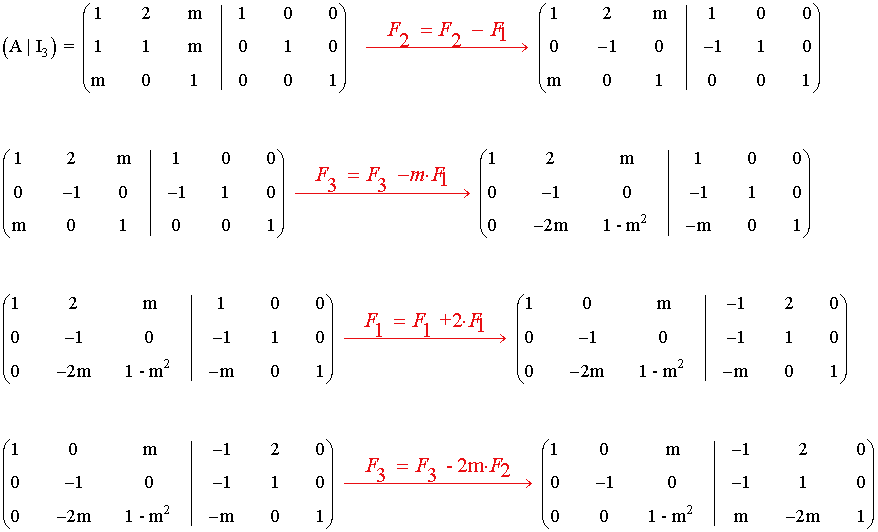
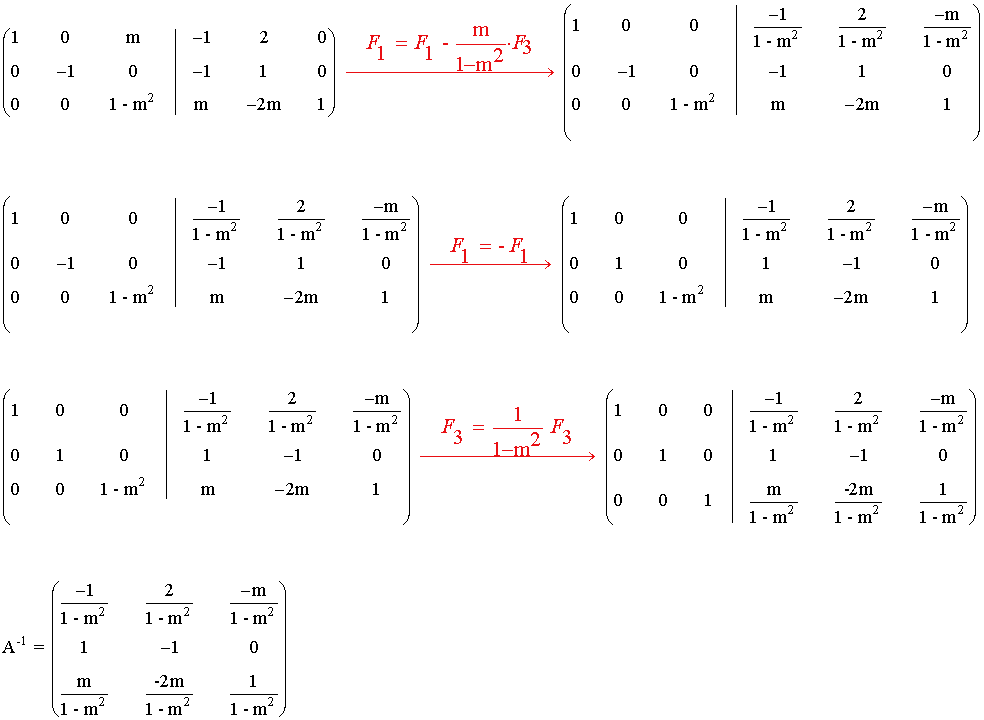
Para poder calcular la inversa tenemos que dividir entre (1 - m2), luego esta expresión no puede ser cero.
Es decir, la matriz A es inversible cuando:
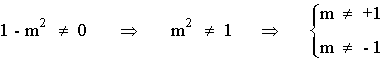
14) Consideremos la matriz A:
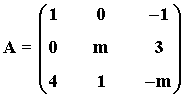
a) Averigua para que valores del parámetro m la matriz no tiene inversa
b) Calcula, si es posible, la matriz inversa de A para m = 2
a) La matriz A tiene inversa si su rango es 3, por lo que transformamos A en una matriz escalonada:
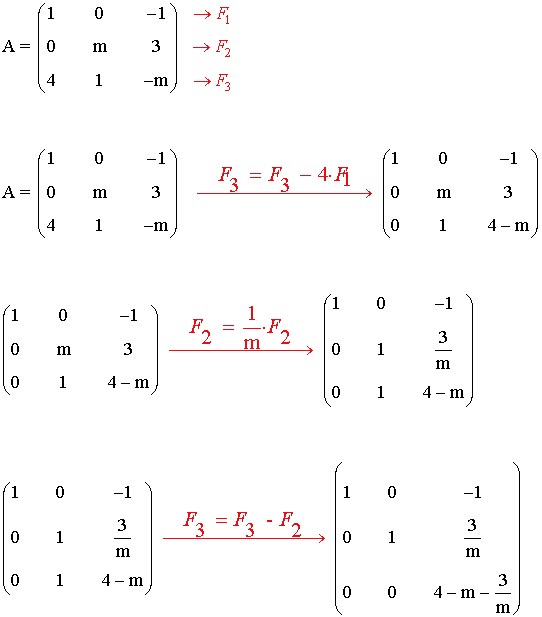
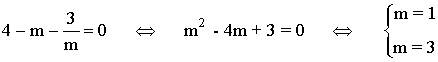
La matriz A no tiene inversa si:
Por lo tanto la matriz A tiene inversa para todo número real m distinto de 1 y 3
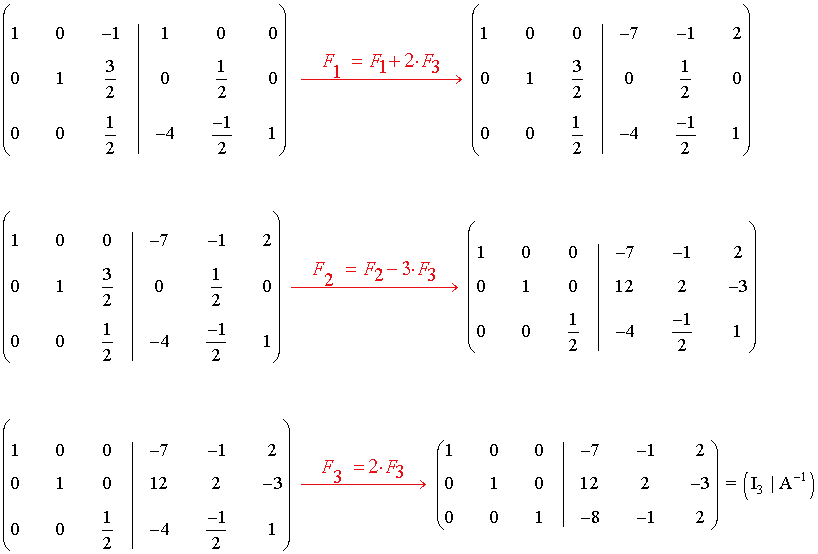
b) Para m = 2 la matriz tiene inversa
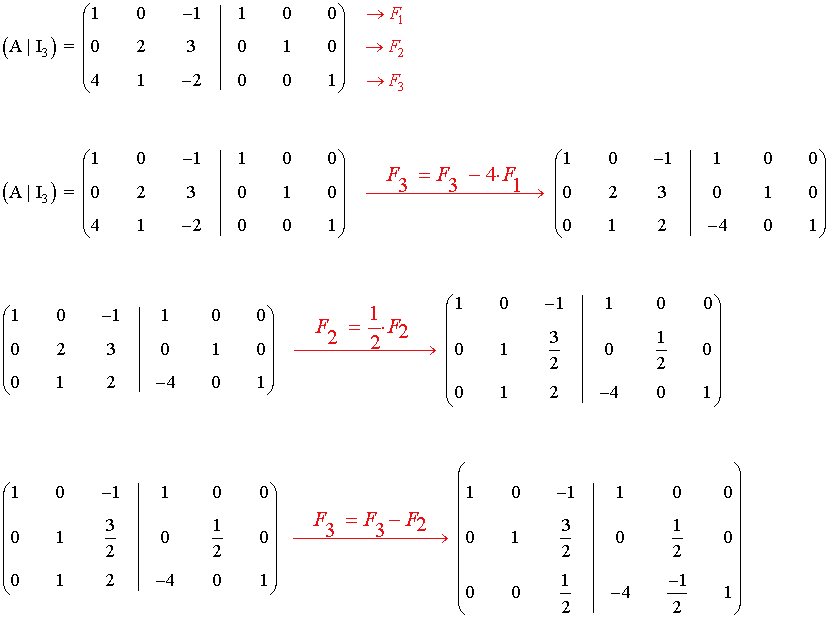
15) Se consideran las matrices:
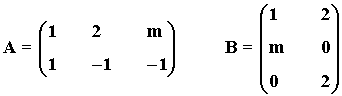
donde m es un número real. Encuentra los valores de m para los que A·B tiene inversa.
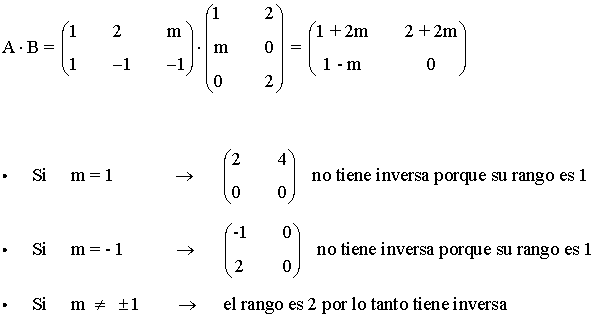
16) Se consideran las matrices:
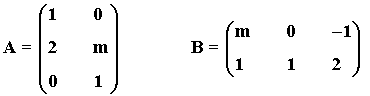
a) Estudia, en función de los valores reales de m , si la matriz B·A tiene inversa
b) Haz lo mismo para la matriz A·B
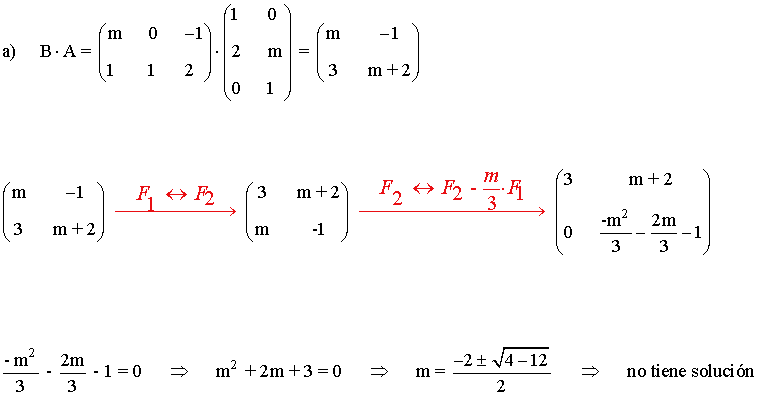
Como no existe ningún valor de m que anule a dicha celda, la matriz B·A siempre tiene rango 2, por lo tanto siempre tiene matriz inversa.

Para cualquier valor de m existe una fila nula en la matriz A·B , es decir, siempre tiene rango 2. Como el rango es menor que la dimensión de la matriz, no existe su matriz inversa sea cual sea el valor de m .


 INICIO
INICIO