Cuádricas
Se llama cuádrica a la superficie que representa cualquier ecuación de segundo grado de la forma:
![]()
Elipsoide
Un elipsoide con centro en el origen y cuyos ejes coinciden con los ejes de coordenadas tiene de ecuación:
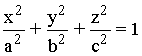
Donde a, b y c son los semiejes dele elipsoide.
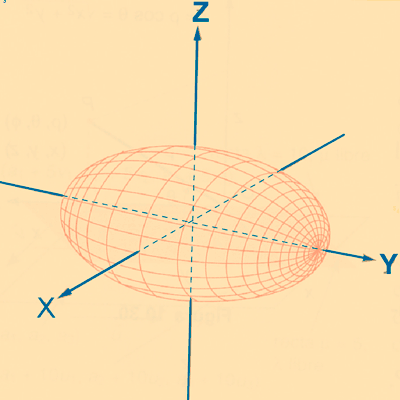
| Plano | Sección |
|---|---|
| Paralelo al plano xy | Elipse |
| Paralelo al plano xz | Elipse |
| Paralelo al plano yz | Elipse |
Ejemplo 1:


Hiperboloide de una hoja
Un hiperboloide de una hoja con centro en el origen y cuyos ejes coinciden con los ejes de coordenadas tiene de ecuación:
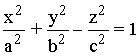
Donde a, b y c son los semiejes del hiperboloide.
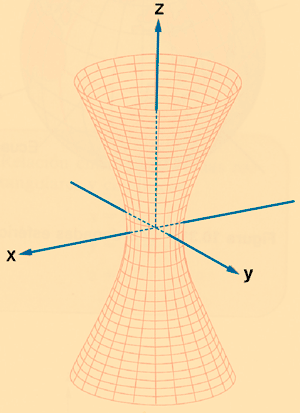
| Plano | Sección |
|---|---|
| Paralelo al plano xy | Elipse |
| Paralelo al plano xz | Hipérbola |
| Paralelo al plano yz | Hipérbola |
Ejemplo 2:
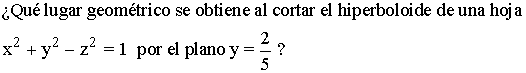

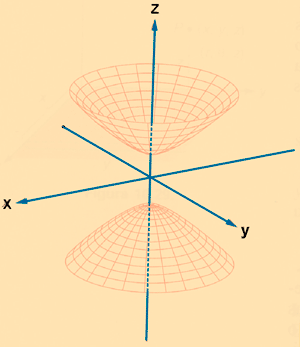
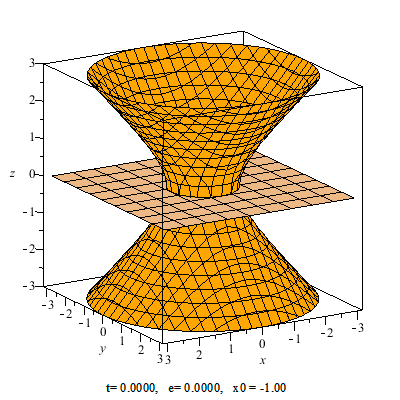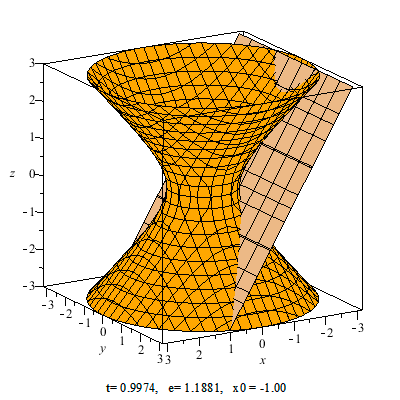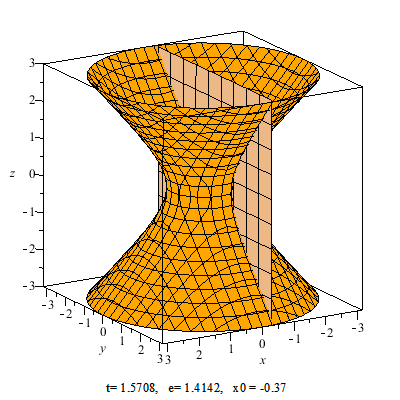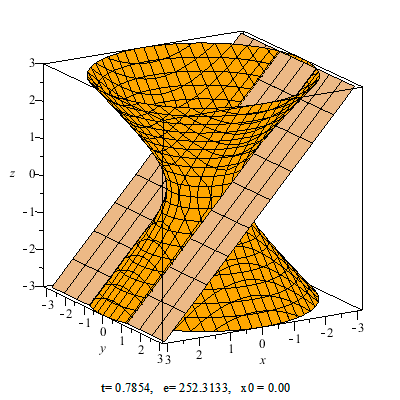
Hiperboloide de dos hojas
Un hiperboloide de dos hojas con centro en el origen y cuyos ejes coinciden con los ejes de coordenadas tiene de ecuación:
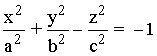
Donde a, b y c son los semiejes del hiperboloide.
| Plano | Sección |
|---|---|
| Paralelo al plano xy | Elipse |
| Paralelo al plano xz | Hipérbola |
| Paralelo al plano yz | Hipérbola |
Ejemplo 3:
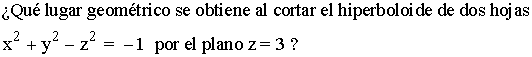

Paraboloide elíptico
Un paraboloide elíptico cuyo eje coincide con el eje de coordenadas Z tiene de ecuación:
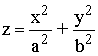
Donde a y b son los semiejes del paraboloide elíptico.
| Plano | Sección |
|---|---|
| Paralelo al plano xy | Elipse |
| Paralelo al plano xz | Parábola |
| Paralelo al plano yz | Parábola |
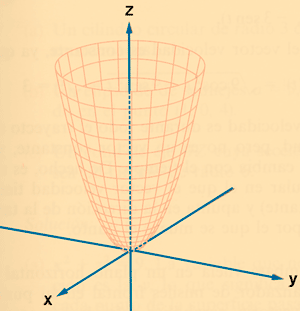
Ejemplo 4:
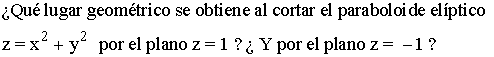

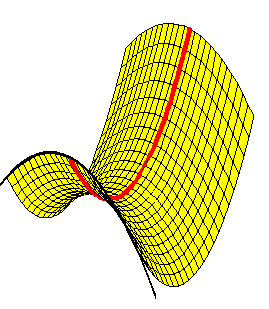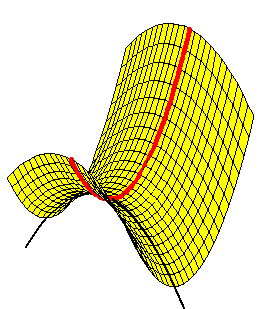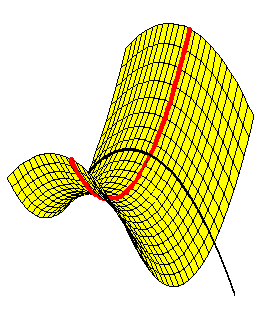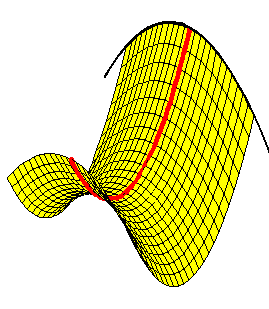
Paraboloide hiperbólico
Un paraboloide hiperbólico de eje Z tiene de ecuación:
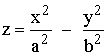
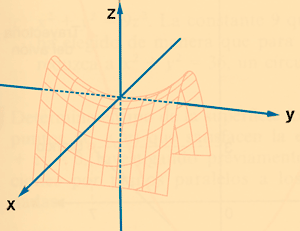
| Plano | Sección |
|---|---|
| Paralelo al plano xy | Hipérbola |
| Paralelo al plano xz | Parábola |
| Paralelo al plano yz | Parábola |
Ejemplo 5:
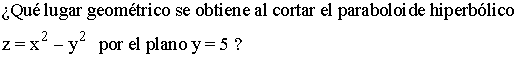

Cuádricas animadas
http://commons.wikimedia.org/wiki/Category:Animations_of_curves


 INICIO
INICIO

