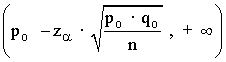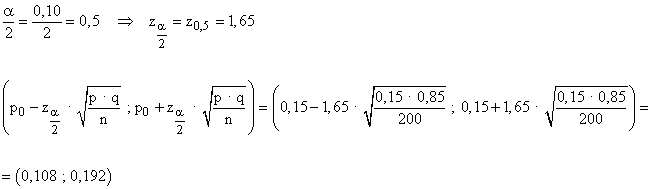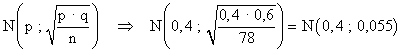Contraste de hipótesis para las proporciones.
Si se quiere contrastar una hipótesis sobre la proporción de individuos de una población a partir de los datos obtenidos en una muestra, un buen estadístico de la proporción poblacional p es la proporción de la muestra ![]() . Si la variable p sigue una distribución binomial, entonces el estadístico
. Si la variable p sigue una distribución binomial, entonces el estadístico ![]() sigue una distribución
sigue una distribución 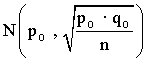 .
.
| Contraste bilateral | Contraste unilateral izquierdo | Contraste unilateral derecho | |
|---|---|---|---|
| Hipótesis | 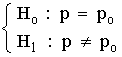 |
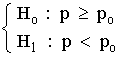 |
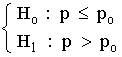 |
| Zona de aceptación | 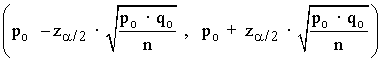 |
|
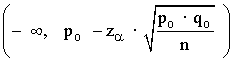 |
| Valores críticos |
Fases en el contraste de hipótesis.
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
3. Construimos las regiones de aceptación y rechazo.
4. Calcular el estadisto de contraste y verificar la hipótesis.
5. Interpretación de la decisión.
Ejemplo 1:
En los últimos meses, una cadena comercial ha intentado potenciar con precios más atractivos y publicidad la venta de productos con la marca genérica de la cadena, frente a los de otras marcas más conocidas por los consumidores. Antes, un 15 % de los productos que vendía eran de la marca de la cadena. Recientemente, en una muestra de 200 productos vendidos, 36 eran de dicha marca.
Plantea un test para contrastar que las medidas no han surtido efecto frente a que sí lo han hecho, como parecen indicar los datos. ¿A qué conclusión se llega con una signifcación del 10 % ?
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
Hipótesis nula : H0 : p = 0,15
Hipótesis alternativa : H1 : p ≠ 0,15
Se trata de un contraste bilateral porque H0 está enunciada en términos de igualdad.2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
Tenemos una distribución en la proporción, con p = 0,15 y un tamaño de muestra n = 200. La proporción se distribuye :
3. Construimos las regiones de aceptación y rechazo.
A partir de un nivel de significación de α = 0,10 vamos a contruir nuestras regiones.
El nivel de confianza es 1 - α = 0,90 y la zona de aceptación se corresponde con el intervalo :
4. Calcular el estadisto de contraste y verificar la hipótesis.
5. Interpretación de la decisión.
Como la proporción muestral pertenece a mi región de aceptación, podemos aceptar que las medidas no han surtido efecto con un nivel de significación del 10 % o un nivel de confianza del 90 %.
Aceptamos por tanto nuestra hipótesis nula.
Ejemplo 2:
Hace 10 años, se hizo un amplio estudio y se concluyó que, como máximo, el 40 % de los estudiantes universitarios eran fumadores. Para ver si actualmente se mantienen las mismas conclusiones, se tomó una muestra de 78 estudiantes entre los que 38 eran fumadores.
Con un nivel de significación del 10 %, ¿se acepta que el porcentaje de fumadores entre los universitarios es menor o igual que el 40% ?
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
Hipótesis nula : H0 : p ≤ 0,4
Hipótesis alternativa : H1 : p > 0,4
Nuestra hipótesis nula está enunciada en forma de inecuación, por lo que tendremos un contraste unilateal.2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
Tenemos una distribución de la proporción, con p = 0,4 y una muestra de tamaño n = 78, cuya distribución es la siguiente :
3. Construimos las regiones de aceptación y rechazo.
A partir de un nivel de significación α = 0,10 y con un nivel de confianza de 1 - α = 0,9 contruimos nuestra región de aceptación. Como es un contraste unilateral, emplearemos zα :
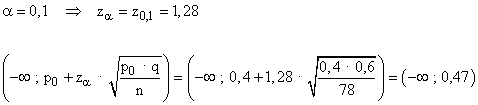
4. Calcular el estadisto de contraste y verificar la hipótesis.
5. Interpretación de la decisión.
Dado que el estadístico de contraste no pertenece a nuestra región de aceptación, rechazamos nuestra hipótesis nula.
Se acepta que el porcentaje de fumadores universitarios ha aumentado.


 INICIO
INICIO