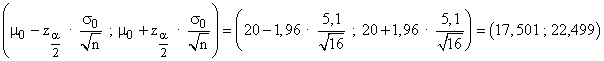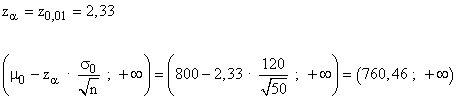INICIOContraste de hipótesis para la media.
Si se quiere contrastar una hipótesis sobre la media poblacional a partir de la media obtenida en una muestra, un buen estadístico para la media poblacional μ es la media muestral . Si la población de partida es normal, con desviación típica conocida, la media muestral sigue una distribución: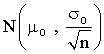 
.
Si la población de estudio no es normal o bien σ es desconocida, pero el tamaño de la muestra es 
podemos tomar la desviación típica de la muestra y entones la media muestral sigue una distribución .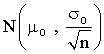
| Contraste bilateral | Contraste unilateral izquierdo | Contraste unilateral derecho | |
|---|---|---|---|
| Hipótesis |  |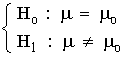
 |
 |
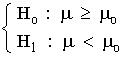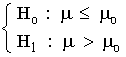| Zona de aceptación |  |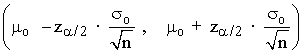
 |
 |
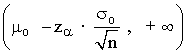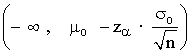| Valores críticos |  |
 |
|
Fases en el contraste de hipótesis.
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
3. Construimos las regiones de aceptación y rechazo.
4. Calcular el estadisto de contraste y verificar la hipótesis.
5. Interpretación de la decisión.
Ejemplo 1:
Los depósitos mensuales, en euros, en una entidad bancaria, siguen una distribución normal de media μ y de desviación típica σ = 5,1. Con el fin de contrastar si la media de los depósitos mensuales es 20 €, se toma una muestra de tamaño 16, resultando ser la media muestral 22,40 €. ¿Se puede aceptar la hipótesis de que la media es 20 a un nivel de significación del 5 %?
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
Hipótesis nula : H0 : μ = 20
Hipótesis alternativa : H1 : μ ≠ 20
Se trata de un contraste bilateral porque H0 está enunciada en términos de igualdad.
Si la hipótesis nula es cierta, la media de la población de partida será μ = 20. Se considera que la diferencia entre el verdadero valor de la media y su valor hipotético es nula.2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
Por el enunciado sabemos que la población inicial sigue una distribución normal. El tamaño de la muestra es n = 16. La media muestral se distribuye :
3. Construimos las regiones de aceptación y rechazo.
A partir de un nivel de significación de α = 0,05 vamos a contruir nuestras regiones.
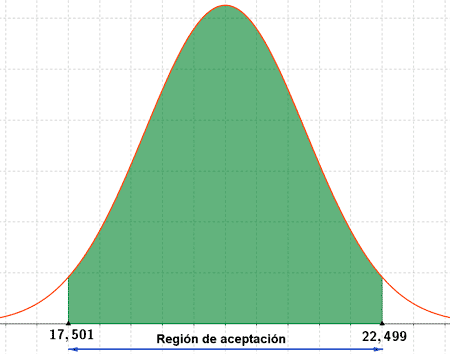
El nivel de confianza es 1 - α = 0,95 y la zona de aceptación se corresponde con el intervalo :
4. Calcular el estadístico de contraste y verificar la hipótesis.
En este caso, el estadístico se encuentra en la región de aceptación.
5. Interpretación de la decisión.
Como la media muestral pertenece a mi región de aceptación, podemos aceptar que el depósito mensual es de 20 € con un nivel de significación del 5 % o un nivel de confianza del 95 %.
Aceptamos por tanto nuestra hipótesis nula.
Ejemplo 2:
La duración de las bombillas de 100 vatios que fabrica una empresa sigue una distribución normal con una desviación típica de 120 horas. Su vida media está garantizada durante un mínimo de 800 horas.
Se escoge al azar una muestra de 50 bombillas de un lote y, después de comprobarlas, se obtiene una media de 750 horas.
Con un nivel de significación de 0,01, ¿habría que rechazar el lote por no cumplir la garantía?
1. Se formula la hipótesis nula H0 y la hipótesis alternativa H1.
Hipótesis nula : H0 : μ ≥ 800
Hipótesis alternativa: H1 : μ < 800
Se trata de un contraste unilateral porque H0 está enunciada como una incecuación.
Si la hipótesis nula es cierta, la media de la población de partida será μ ≥ 800. Se considera que la diferencia entre el verdadero valor de la media y su valor hipotético es nula.2. Identificamos la distribución de probabilidad y el tamaño de la muestra.
Por el enunciado sabemos que la población inicial sigue una distribución normal. El tamaño de la muestra es n = 50. La media muestral se distribuye :
3. Construimos las regiones de aceptación y rechazo.
A partir de un nivel de significación de α = 0,01 vamos a contruir nuestras regiones.
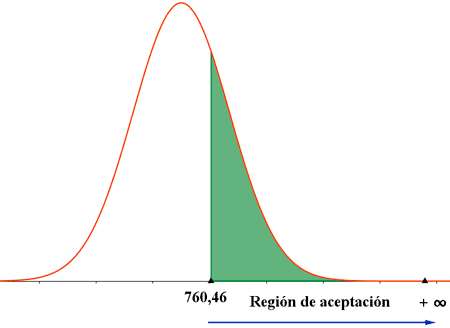
El nivel de confianza es 1 - α = 0,99 y la zona de aceptación se corresponde con el intervalo :
4. Calcular el estadisto de contraste y verificar la hipótesis.
5. Interpretación de la decisión.
Como la media muestral no pertenece a mi región de aceptación, tenemos que rechazar el lote, con un nivel de significación del 1 % o un nivel de confianza del 99 %.
Rechazamos por tanto nuestra hipótesis nula.
