INICIOTeoremas sobre funciones derivables
Regla de L'Hôpital
Sean f y g funciones derivables en algún intervalo abierto que contiene al punto a .
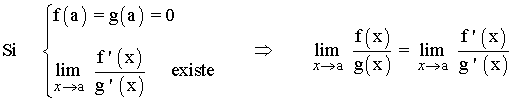
En resumen:
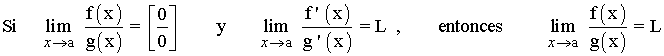
Ejemplo de la regla de L'Hôpital:
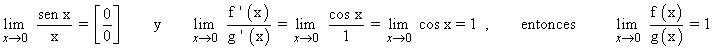
Ampliación de la regla de L'Hôpital
En los casos de indeterminacion:
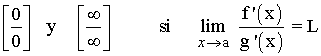
donde L es un número real , +∞ o -∞ , entonces se cumple que:
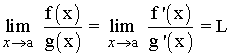
Ejemplo de la ampliación de la regla de L'Hôpital
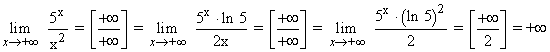
Aplicación de L'Hôpital para el resto de indeterminaciones
Las restantes indeterminaciones ∞·0 , 0·∞ , ∞ - ∞ , 1∞ , ∞0 , 00 hay que pasarlas a la forma:
para poder aplicar la regla de L'Hôpital .
Indeterminaciones ∞·0 y 0·∞
Ejemplo:
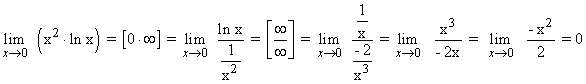
Pasamos de la indeterminación 0·∞ a ∞/∞ aplicando el inverso del inverso a la parte que tiende a 0 .
Indeterminación ∞ - ∞
Ejemplo:
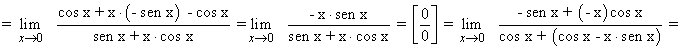
Pasamos de la indeterminación ∞ - ∞ a 0/0 transformando la expresión a común denominador y aplicando la regla de L'Hôpital dos veces.
Indeterminaciones 1∞ , ∞0 , 00
Ejemplo:
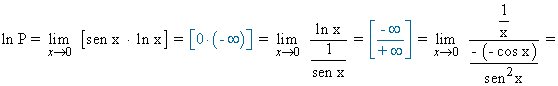
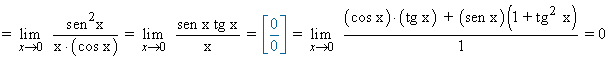
ln P = 0 ⇔ P = e0 = 1
