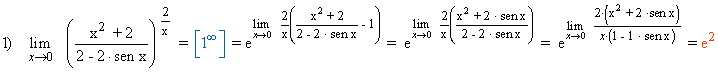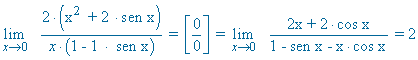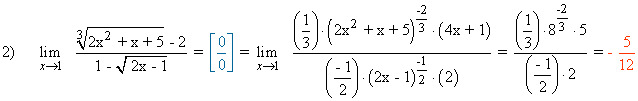Ejercicios resueltos de la regla de L'Hôpital
SELECTIVIDAD
Calcula los siguientes límites aplicando la regla de L'Hôpital:
![]()
![]()
![]()
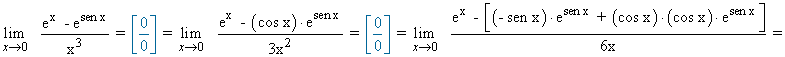
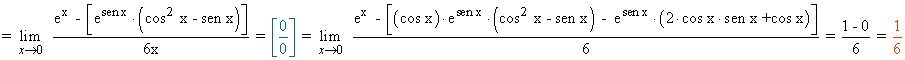
![]()
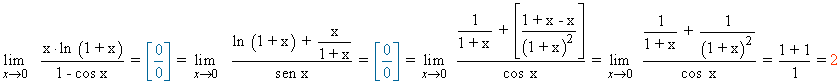
![]()
![]()
![]()
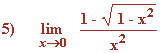
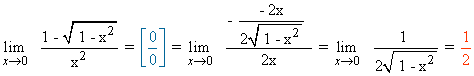
SELECTIVIDAD
Calcula los siguientes límites aplicando la regla de L'Hôpital:
![]()
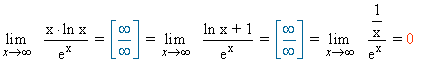
![]()
![]()
SELECTIVIDAD
Calcula los siguientes límites aplicando la regla de L'Hôpital:
![]()
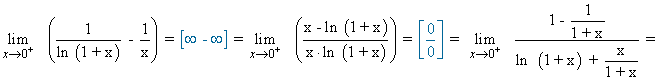
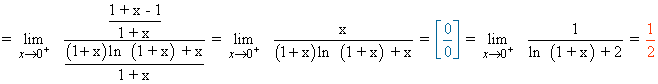
![]()
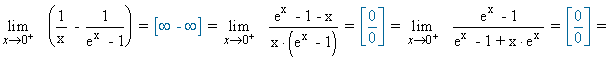
![]()
![]()
![]()
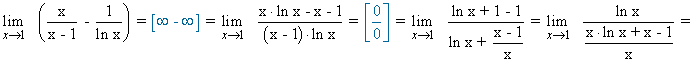
![]()
SELECTIVIDAD
Calcula los siguientes límites aplicando la regla de L'Hôpital:
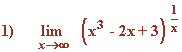
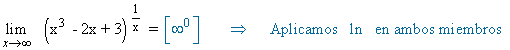
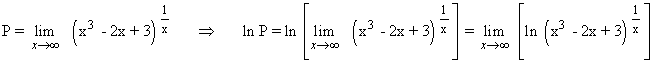
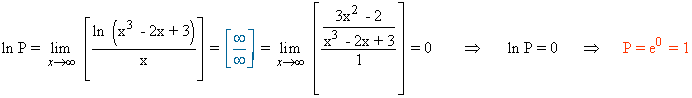
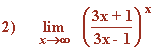

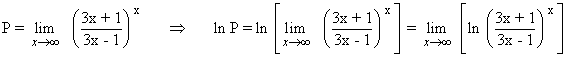
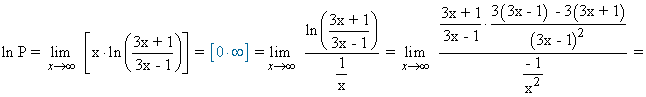
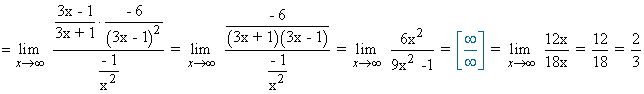
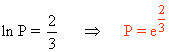
![]()
![]()
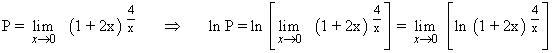
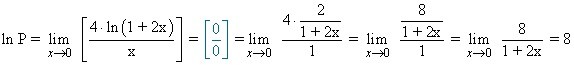
![]()
SELECTIVIDAD
Calcula los siguientes límites:
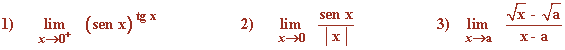
![]()
![]()
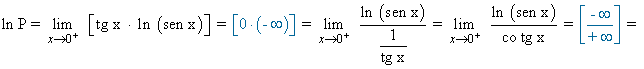
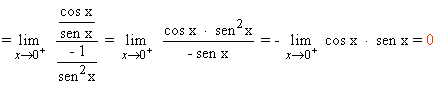
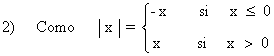
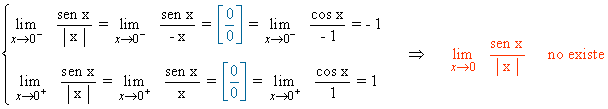
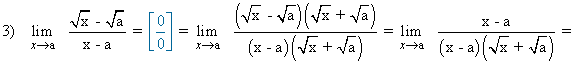
![]()
No es necesario aplicar la regla de L'Hôpital porque se resuelve multiplicando numerador y denominador por el conjugado.
Ver ejercicios resueltos de este tipo.
SELECTIVIDAD
Calcula los siguientes límites:
![]()
1) Para calcular este límite no es necesario aplicar la regla de L'Hôpital porque se resuelve multiplicando numerador y denominador por el conjugado.
Ver ejercicios resueltos de este tipo.
2) Como la función ex se comporta de manera distinta en -∞ y en +∞ , estudiamos los límites laterales:
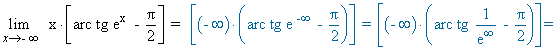
![]()
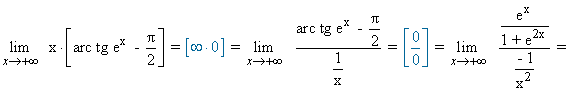
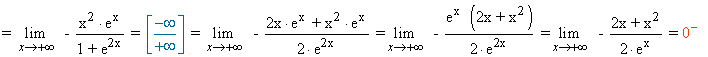
SELECTIVIDAD
Calcula los valores de λ ≠ 0 para los cuales:
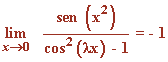
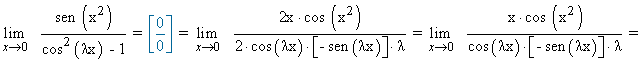
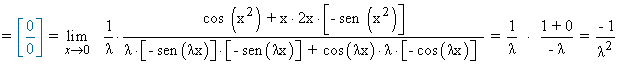
Por lo tanto, el valor de λ para que el límite valga - 1 es:
![]()
Calcula los valores de a y b para los cuales:
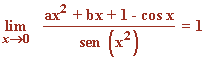
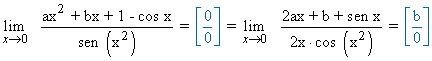
Como el límite debe valer 1 (límite finito) se tiene que cumplir que b = 0
(para cualquier otro valor de b el límite sería ±∞)
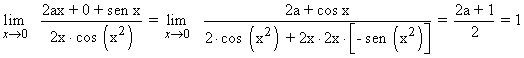
Por lo tanto, el valor de a es:
![]()
SELECTIVIDAD
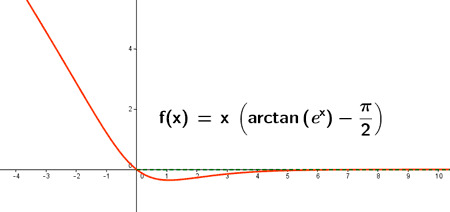
Determina las asíntotas horizontales de la siguientes funciones hallando su dominio y las discontinuidades:
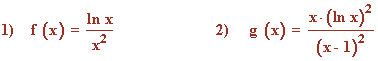
1) El dominio de la función f(x) es (0, +∞) . Por lo tanto estudiamos el límite cuando la función tiende a +∞ :
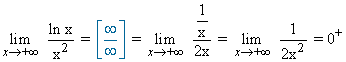
Por lo tanto, la función f(x) tiene una asíntota horizontal y = 0 quedando la gráfica por encima de la asíntota.
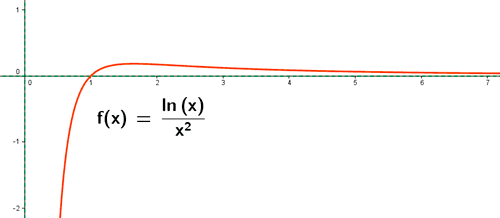
2) El dominio de la función g(x) es (0, 1) ∪ (1, +∞) , puesto que la función ln x está definida en el intervalo (0, +∞) y porque el denominador se anula para x = 1 .
Ocurre que la función en el punto x = 1 toma el siguiente valor:
![]()
Es decir, la función en este punto se anula tanto en el numerador como en el denominador.
La función no tiene asíntota vertical en x = 1 sino una discontinuidad evitable según se demuestra aplicando la regla de L'Hôpital:
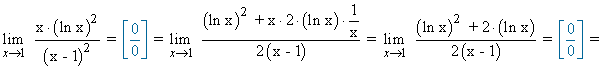
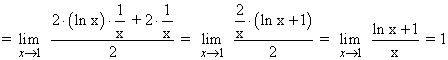
Por lo tanto, aunque la función no esté definida en x = 1 se podría extender por continuidad en x = 1 dándole el valor 1 , dado que se trata de una discontinuidad evitable.
Por último, estudiamos las asíntotas horizontales de la función, es decir, el límite cuando la función tiende a +∞ puesto que según el dominio, la función no está definida para valores negativos::
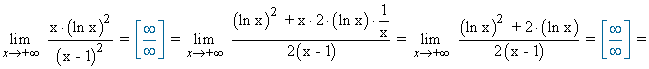
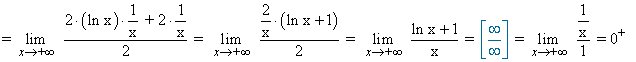
Por lo tanto, la función g(x) tiene una asíntota horizontal y = 0 quedando la gráfica por encima de la asíntota.
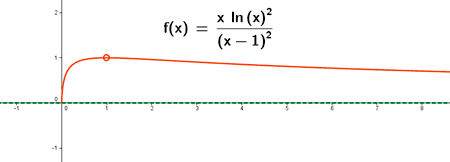
SELECTIVIDAD
Halla los puntos de discontinuidad de la función, donde x está expresado en radianes:
![]()
Para hallar el dominio de la función, estudiamos por separado el dominio del numerador y del denominador. El dominio de la función tangente es el siguiente:
![]()
Por otra parte, el denominador se anula para x = 0 , por lo que se puede concluir que:
![]()
Ocurre que la función en el punto x = 0 toma el siguiente valor:
![]()
Es decir, la función en este punto se anula tanto en el numerador como en el denominador.
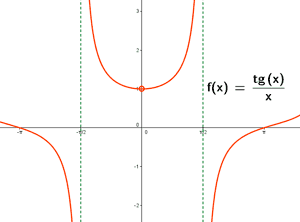
La función no tiene asíntota vertical en x = 0 sino una discontinuidad evitable según se demuestra aplicando la regla de L'Hôpital:
![]()
Por lo tanto, aunque la función no esté definida en x = 0 se podría extender por continuidad en x = 0 dándole el valor 1 , dado que se trata de una discontinuidad evitable.
SELECTIVIDAD
Sea f una función definida por:
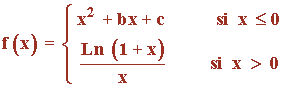
a) Obtener c para que f sea continua en x = 0 .
b) Obenter b para que f sea derivable en x = 0 .
a) Obtener c para que f sea continua en x = 0 .
Para que f sea continua en x = 0 los límites laterales tienen que coincidir con f(0) :
f(0) = 0 + 0 + c = c
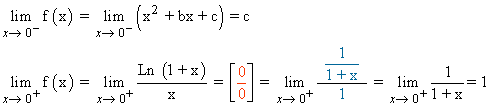
Para resolver la indeterminación 0/0 hemos aplicado la regla del l'Hôpital.
Por tanto: c = 1
b) Obenter b para que f sea derivable en x = 0 .
Para que f sea derivable en x = 0 , las derivadas laterales en dicho punto tienen que coincidir.
Si x ≤ 0 : f(x) = x2 + bx + c ⇒ f '(x) = 2x + b
f '(0- ) = b
Si x > 0 :
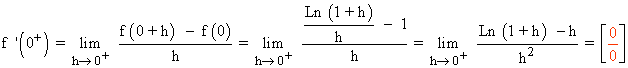
Para resolver la indeterminación aplicamos la regla de l'Hôpital dos veces:
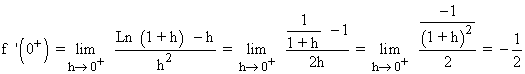
Por tanto, f es derivable en x = 0 si :
f '(0- ) = f(0+ ) ⇔ b = - 1/2
Para calcular la derivada lateral en 0+ hemos aplicado la definición de derivada en un punto, pero tambíen podríamos haber calculado la derivada por la regla correspondiente y depués haber hallado el límite.
Para calcular dicho límite habrá que aplicar dos veces la regla de l'Hôpital.
Conclusión:
Si c = 1 y b = -1/2 la función es continua y derivable en x = 0.


 INICIO
INICIO