Problemas resueltos de volúmenes
1) Calcular, por integrales, el volumen de un cono cuya base tiene por radio r y por altura h.
2) Calcular, por integrales, el volumen de un cilindro cuya base tiene por radio r y por altura h.
3) Deducir por integración que el volumen de una esfera de radio r es:
![]()
4) Calcular el volumen del elipsoide de revolución engendrado por la elipse
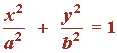
al girar alrededor de su eje mayor 2a.
5) Deducir por integración que la fórmula del volumen de un tronco de cono de altura h y radios r y R es:
![]()
6) Calcular, por integrales, el volumen del segmento esférico de una o dos bases.
7) El toro de revolución es el sólido generado por una circunferencia al girar alrededor del eje OX. Calcular el volumen del toro de revolución generado por la circunferencia
x2+(y - b)2 = r2 (b > r > 0) al girar alrededor del eje OX.
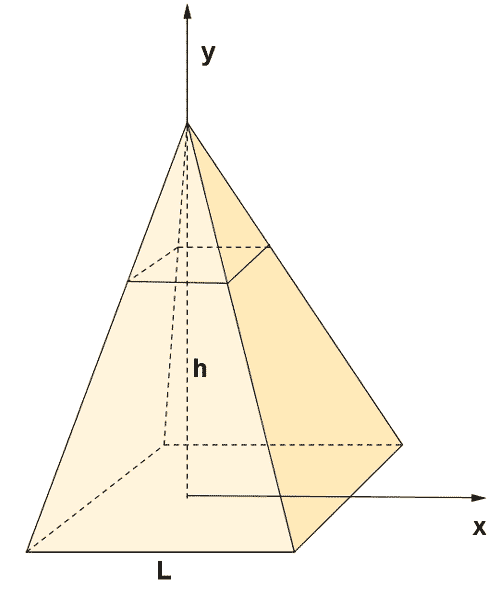
8) Comprueba que el volumen de una pirámide con base cuadrada de lado L y altura h es
![]()
9) Calcular el volumen limitado por el elipsoide de revolución generado por la elipse
2x2 + y2 = 1
al girar alrededor del eje OX.
10) Hallar el volumen engenderado por la revolución entorno del eje OX del recinto limitado por la curva y = sen(x) y el segmento de dicho eje comprendido entre 0 y π
11) Hallar el volumen del toro de revolución que se obtiene al girar la circunferencia
x2+(y - 2)2 = r2 alrededor del eje OX.
12) Hallar el volumen engendrado al girar la superficie comprendida entre las curvas y = sen(x), y = cos (x) y la recta x=0.
13) Hallar el volumen del sólido engendrado al girar alrededor del eje OX el recinto limitado por las curvas f(x) = √x y g(x) = x2 .
14) Calcular el volumen engendrado al girar al rededor de la recta x = 2 el recinto plano limitado por la parábola y2 = 8x.
15) Calcular el volumen del sólido que engendra al girar alrededor del eje OX la región comprendida entre dicho eje y la gráfica de la función
1) Calcular, por integrales, el volumen de un cono cuya base tiene por radio r y por altura h.
El cono puede generarse tomando una segmento que pasa por el origen y por el punto ( h, r ) y rotándolo sobre el eje de abscisas tal como se aprecia en la figura.
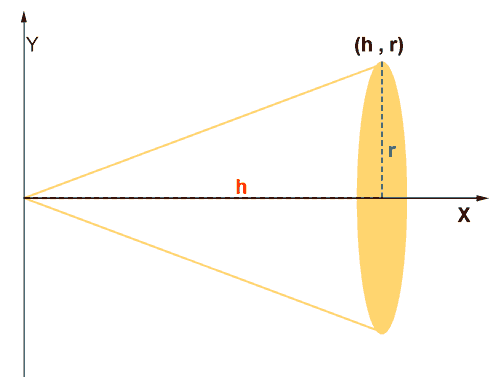
Para calcular el volumen necesitamos una fórmula para los puntos del segmento. Dados dos puntos ( x0, y0 ), ( x1, y1 ) la recta que pasa por los mismos vendrá dada por la ecuación:
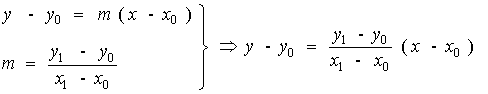
En nuestro caso ( x0, y0 ) = ( 0, 0 ), ( x1, y1 ) = ( h , r ), de manera que
![]()
Teniendo en cuenta esta expresión, el volumen del cono se calcula de la siguiente forma:
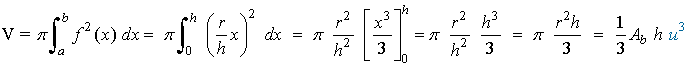
donde Ab = πr2 es el área de la base del cono. Por tanto, el volumen es igual a un tercio del área de la base por la altura.
2) Calcular, por integrales, el volumen de un cilindro cuya base tiene por radio r y por altura h.
El cilindro puede generarse tomando una segmento que pasa por el los puntos ( 0, h ) y ( h, r ) y rotándolo sobre el eje de abscisas tal como se aprecia en la figura.
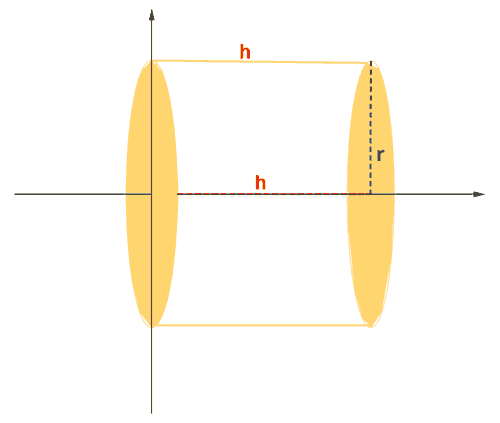
Para calcular el volumen necesitamos una fórmula para los puntos del segmento, que en este caso es claramente y = r
Teniendo en cuenta esta expresión, el volumen del cilindro se calcula de la siguiente forma:
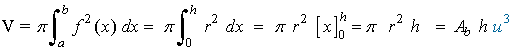
donde Ab = πr2 es el área de la base del cilindro. Por tanto, el volumen del cilindro es igual al producto de su base por su altura.
3) Deducir por integración que el volumen de una esfera de radio r es:
![]()
La esfera puede generarse haciendo girar una semicircunferencia sobre el eje de abscisas.
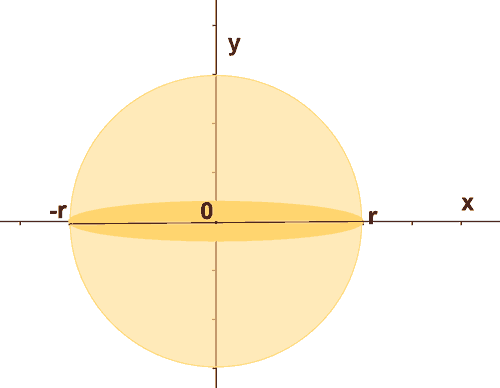
Para calcular el volumen necesitamos una fórmula para los puntos de dicha circunferencia.
La ecuación de la circunferencia de radio r es x2+y2 = r2, de manera que la ecuación que necesitamos es y2 = r2 - x2
Teniendo en cuenta esta expresión, el volumen de la esfera se calcula de la siguiente forma:
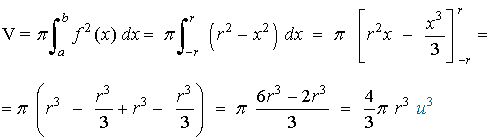
4) Calcular el volumen del elipsoide de revolución engendrado por la elipse
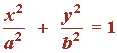
al girar alrededor de su eje mayor 2a.
La esfera puede generarse rotando una semielipse sobre el eje de abscisas.
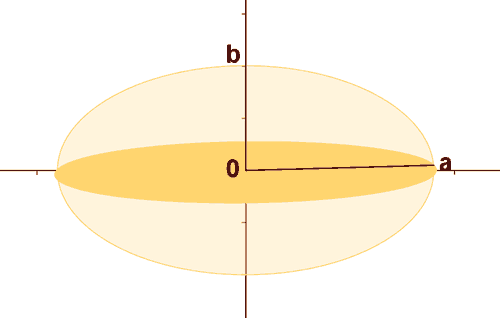
Para calcular el volumen necesitamos una fórmula para los puntos de semielipse. Para ello basta con despejar y2 en la expresión de la elipse.
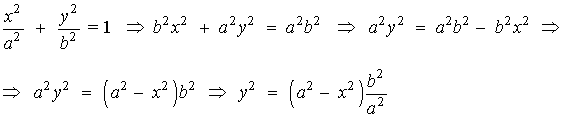
Teniendo en cuenta esta expresión, el volumen de la esfera se calcula de la siguiente forma:
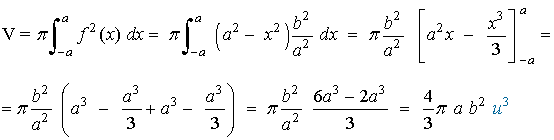
Observamos que si a = b, la elipse es una circunferencia y la fórmula obtenida en este caso es la del volumen de la esfera.
5) Deducir por integración que la fórmula del volumen de un tronco de cono de altura h y radios r y R es:
![]()
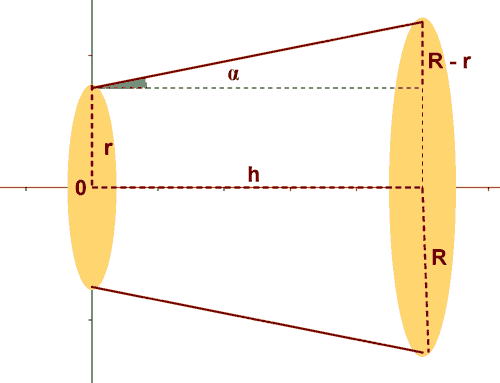
La recta que genera el tronco de cono tiene como pendiente
![]()
y pasa por el punto ( 0, r ) de manera que la ecuación de los puntos de dicha recta es:
![]()
Teniendo en cuenta esta expresión, el volumen del cono se calcula de la siguiente forma:
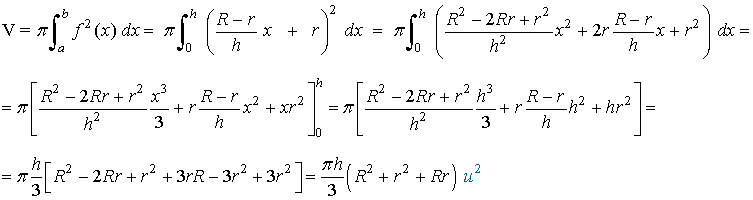
6) Calcular, por integrales, el volumen del segmento esférico de una o dos bases.
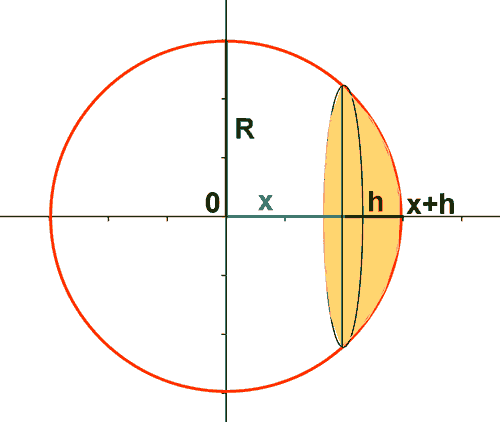
Un segmento esférico se engendra girando alrededor del eje de abcisas el un segmento de circunferencia de centro origen y radio R. La ecuación de la circunferencia de radio R es x2+y2 = R2, de manera que la ecuación que necesitamos es y2 = R2 - x2 con x∈[x, x+h] con 0<h. Teniendo esto en cuenta:
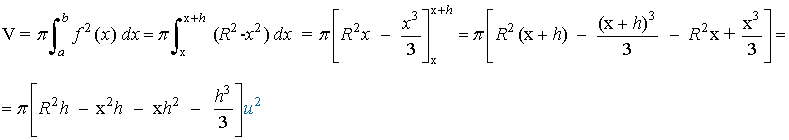
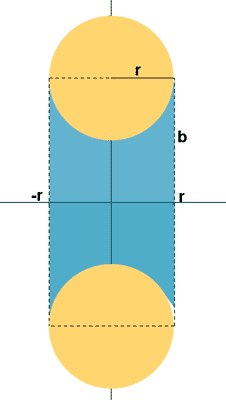
7) El toro de revolución es el sólido generado por una circunferencia al girar alrededor del eje OX. Calcular el volumen del toro de revolución generado por la circunferencia
x2+(y - b)2 = r2 (b > r > 0) al girar alrededor del eje OX.

La cirfunferencia admite una expresión a partir de dos funciones:
![]()
el volumen del toro será la diferencia de hacer girar alrededor del eje OX el volumen engendrado por el recinto delimitado por el eje OX, las rectas x = -r, x = r y
![]()
y restarle el volumen engendrado por el recinto delimitado por el eje OX, las rectas x = -r, x = r y
![]()
Intuitivamente, podemos pensar en el toro como en la cámara de un neumático. Al calcular el volumen engendrado por el primer recinto obtendríamos la rueda completa, llanta y cámara. El volumen de la llanta vendría dado por el segundo recinto, de manera que al restarselo a la rueda completa, nos quedaría únicamente el volumen de la cámara, es decir, del toro.
Teniendo estas ideas presentes el volumen que nos piden calcular es el siguiente:
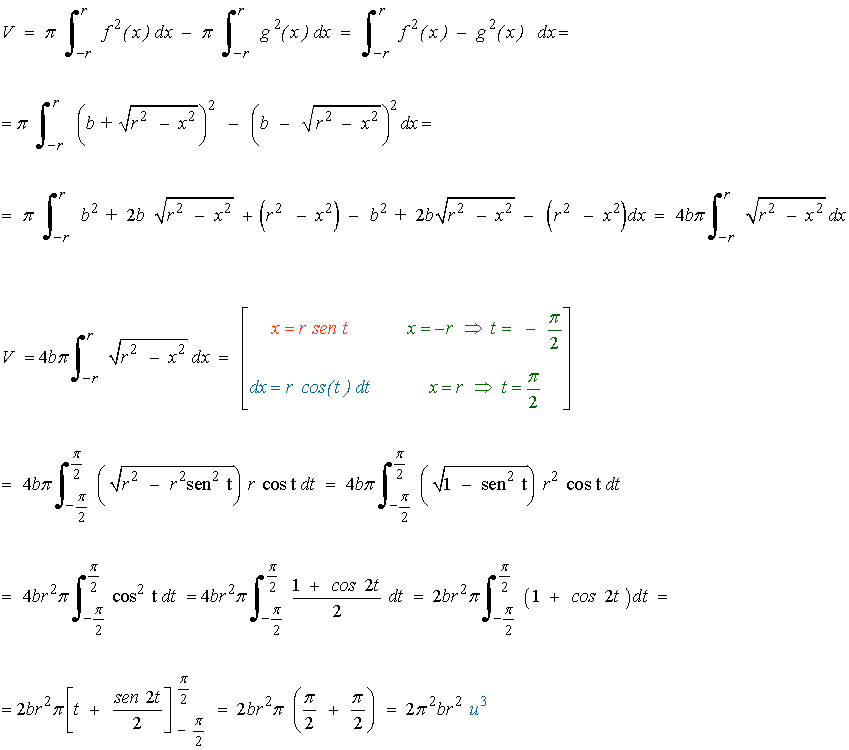
8) Comprueba que el volumen de una pirámide con base cuadrada de lado L y altura h es
![]()

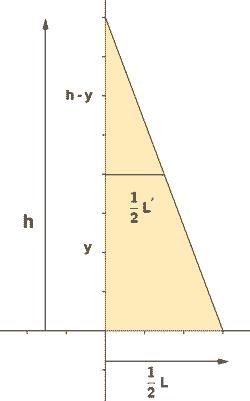
A partir de la figura, por el teorema de Tales,
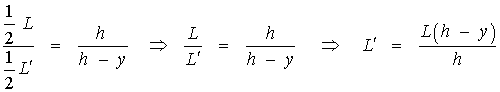
de manera que el área de las secciones transversales es,
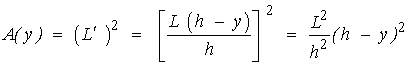
De manera que integrando entre 0 y h obtenemos que
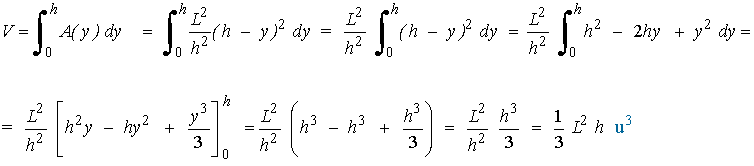
9) Calcular el volumen limitado por el elipsoide de revolución generado por la elipse
2x2 + y2 = 1
al girar alrededor del eje OX.
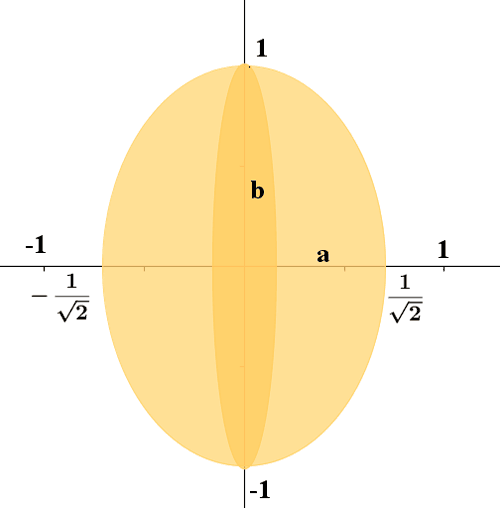
La elipse cuya fórmula nos dan tiene como semiejes a

Observamos que el volumen que nos piden será el doble del que que genera el arco contenido en el primer cuadrante que puede apreciarse en la gráfica. Teniendo en cuenta además que de la ecuación dada obtenemos que y2 = 1 - 2x2 el volumen que nos piden calcular es
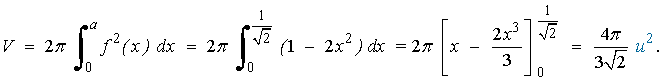
10) Hallar el volumen engenderado por la revolución entorno del eje OX del recinto limitado por la curva y = sen(x) y el segmento de dicho eje comprendido entre 0 y π
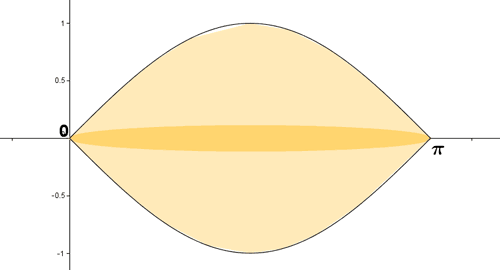
El volumen que nos piden calcular es el siguiente:
11) Hallar el volumen del toro de revolución que se obtiene al girar la circunferencia
x2+(y - 2)2 = r2 alrededor del eje OX.
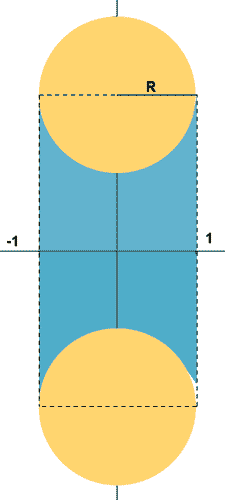

Como
![]()
el volumen del toro será la diferencia de hacer girar alrededor del eje OX el volumen engendrado por el recinto delimitado por el eje OX, las rectas x=-1, x=1 y
![]()
y restarle el volumen engendrado por el recinto delimitado por el eje OX, las rectas x=-1, x=1 y
![]()
Intuitivamente, podemos pensar en el toro como en la cámara de un neumático. Al calcular el volumen engendrado por el primer recinto obtendríamos la rueda completa, llanta y cámara. El volumen de la llanta vendría dado por el segundo recinto, de manera que al restarselo a la rueda completa, nos quedaría únicamente el volumen de la cámara, es decir, del toro.
Teniendo estas ideas presentes el volumen que nos piden calcular es el siguiente:
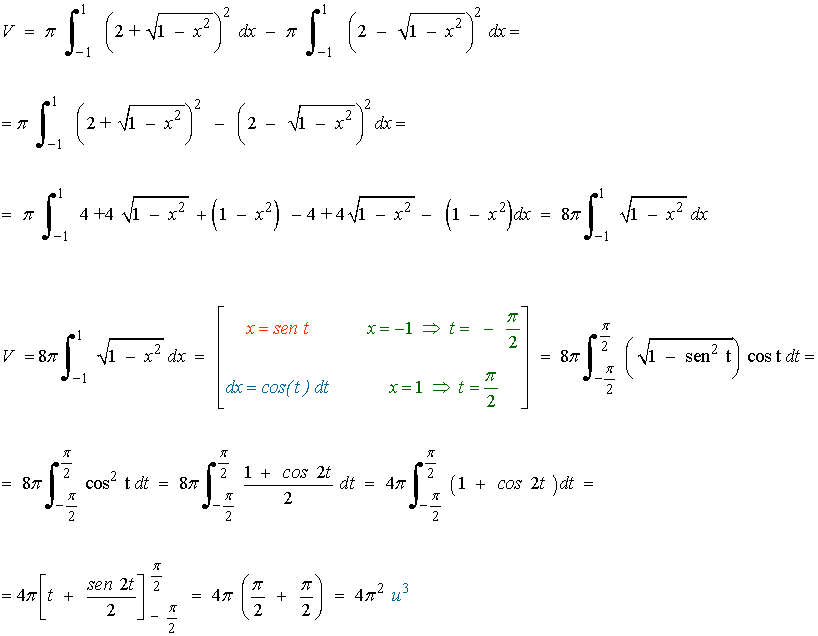
12) Hallar el volumen engendrado al girar la superficie comprendida entre las curvas y = sen(x), y = cos (x) y la recta x=0.
Intersección de las curvas
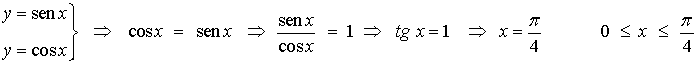
De manera que las curvas se cortan en el punto de abscisa π/4. La gráfica muestra el recinto cuyo volumen como cuerpo de revolución queremos calcular:
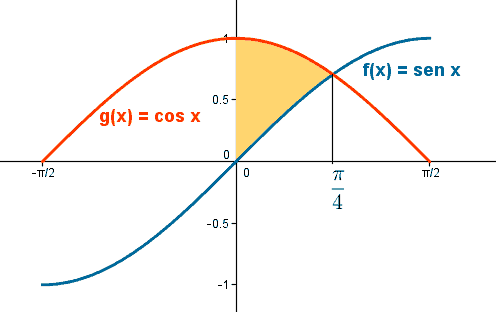
En el intervalo [ 0, π/4 ] se verifica que sen(x) < cos(x) de manera que
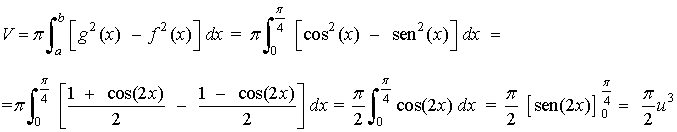
13) Hallar el volumen del sólido engendrado al girar alrededor del eje OX el recinto limitado por las curvas f(x) = √x y g(x) = x2 .

En el intervalo [0, 1] la curva f(x) = √x está por encima de la curva g(x) = x2 .
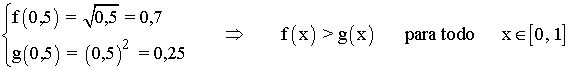
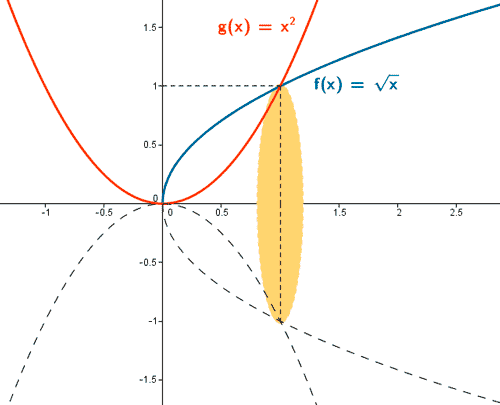
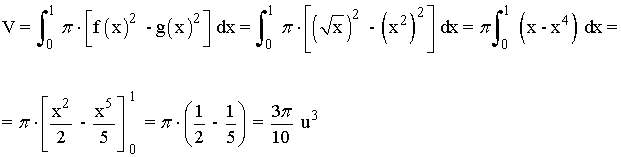
14) Calcular el volumen engendrado al girar al rededor de la recta x = 2 el recinto plano limitado por la parábola y2 = 8x.
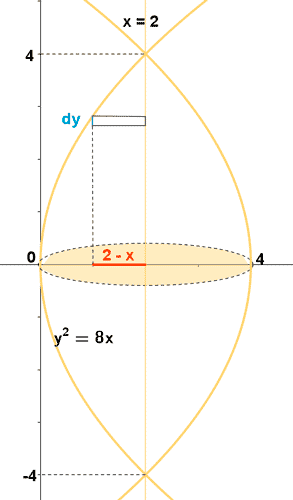
Vamos a empezar por calcular el área de las secciones. Las secciones tienen forma circular y radio 2 - x de manera que sus áreas son π(2 - x)2 o sustituyendo a x por su valor respecto a y,
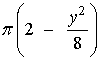
Puntos de intersección
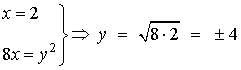
Los puntos de intersección anteriores nos dan los límites de integración.
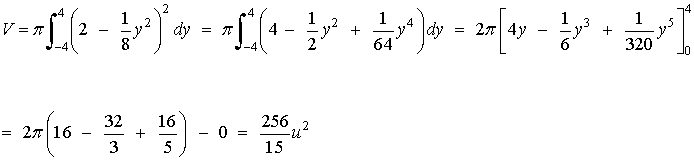
15) Calcular el volumen del sólido que engendra al girar alrededor del eje OX la región comprendida entre dicho eje y la gráfica de la función
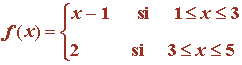
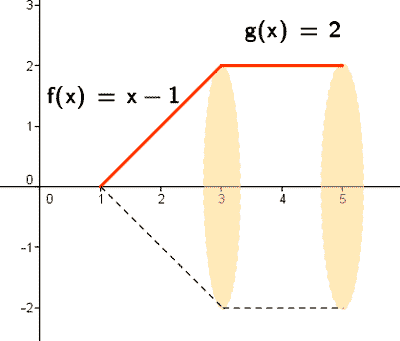
Es lo mismo calcular el volumen engendrado por una curva al girar alrededor del eje OX que calcular el volumen de segmentos disjuntos de dicha curva girando alrededor del eje OX y después sumarlos todos. Teniendo esto en cuenta:


 INICIO
INICIO