Interpretación geométrica de la integral indefinida
Como vimos en temas anteriores la primitiva de una función no es única, ya que existen infinitas primitivas, diferenciandose entre ellas en una constante. Es decir, si F(x) es una primitiva de f(x) , existe todo un conjunto de primitivas (o integrales indefinidas): F(x) + C
De esta forma, si representamos la primitiva F(x) , cada función de la forma F(x) + C resulta una traslación vertical de valor C de la función F(x).
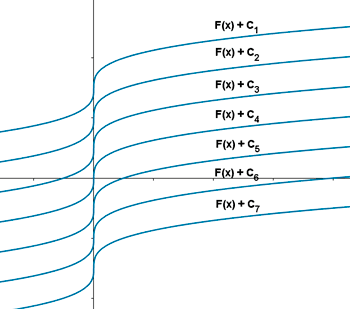
Ejemplos:
1) Halla dos primitivas de la siguiente función:
![]()
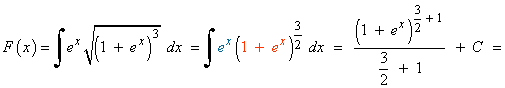
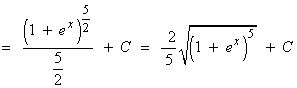
Por lo tanto, dos primitivas de la función f(x) son:
![]()
2) Dada la siguiente función, halla la primitiva F de f que cumple que F(1) = 1
![]()
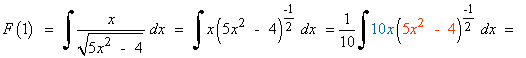
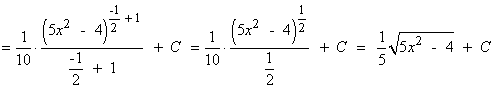
Como la primitiva debe cumplir que F(1) = 1 , tenemos que:
![]()
![]()
Por lo tanto, la primitiva que nos piden es:
![]()
3) Halla f(x) sabiendo que f(0) = 1 , f ' (0)=2 y f '' (x) = 3x
![]()
![]()
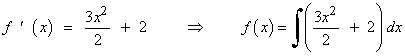
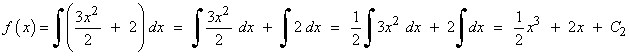
![]()


 INICIO
INICIO

