Ejercicios resueltos de la interpretación
geométrica
de la integral indefinida
1) Sea f la función definida por:
![]()
Calcula la primitiva de f cuya gráfica pasa por el punto (1, e2)
2) Dada la función f definida por:
![]()
Calcúlese una función primitiva de f(x) que pase por el punto P(e, 2)
3) Dada la función f definida por:
![]()
Halla la primitiva de f cuya gráfica pasa por el origen de coordenadas.
4) Dada la siguiente función , halla la primitiva F de f que cumple que F(1) = 1
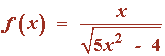
5) Halla f(x) sabiendo que f(0) = 1 , f ' (0)=2 y f '' (x) = 3x
6) Determina f(x) sabiendo que f ''' (x) = 24x , f '' (0) = 2 , f ' (0) = 1 y f (0) = 0
7) Calcula f(x) sabiendo que la función y = f(x) es continua , que f(0)=0 y , además , que su derivada es:
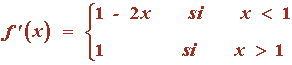
1) Sea f la función definida por:
![]()
Calcula la primitiva de f cuya gráfica pasa por el punto (1, e2)
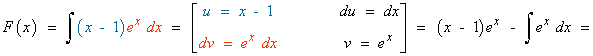
![]()
![]()
![]()
2) Dada la función f definida por:
![]()
Calcúlese una función primitiva de f(x) que pase por el punto P(e, 2)
![]()
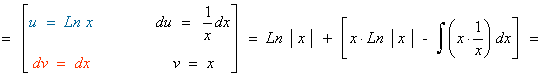
![]()
![]()
![]()
![]()
![]()
3) Dada la función f definida por:
![]()
Halla la primitiva de f cuya gráfica pasa por el origen de coordenadas.
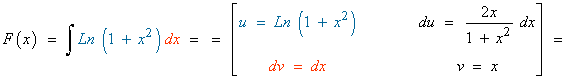
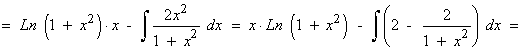
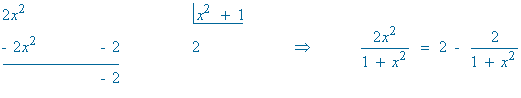
![]()
![]()
![]()
4) Dada la siguiente función , halla la primitiva F de f que cumple que F(1) = 1
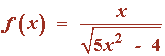
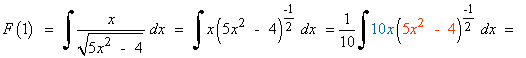
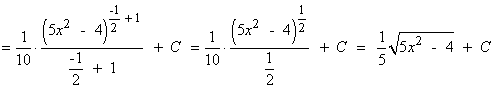
Como la primitiva debe cumplir que F(1) = 1 , tenemos que:
![]()
![]()
Por lo tanto, la primitiva que nos piden es:
![]()
5) Halla f(x) sabiendo que f(0) = 1 , f ' (0)=2 y f '' (x) = 3x
![]()
![]()
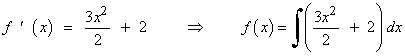
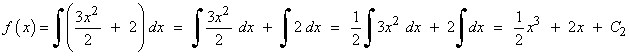
![]()
6) Determina f(x) sabiendo que f ''' (x) = 24x , f '' (0) = 2 , f ' (0) = 1 y f (0) = 0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
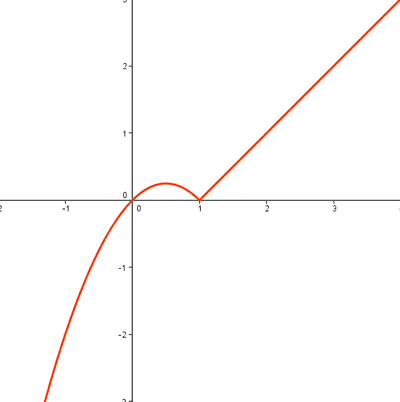
7) Calcula f(x) sabiendo que la función y = f(x) es continua , que f(0)=0 y , además , que su derivada es:
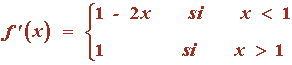
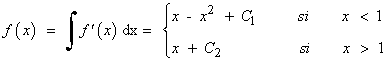
![]()
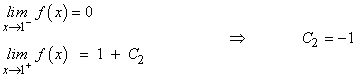
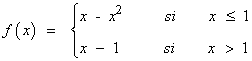


 INICIO
INICIO