Problemas y ejercicios de continuidad de funciones I
Estudiar la siguiente gráfica:
a) Dominio.
b) Recorrido.
c) Extremos absolutos y relativos.
d) Discontinuidades y su clasificación.
e) Asíntotas.
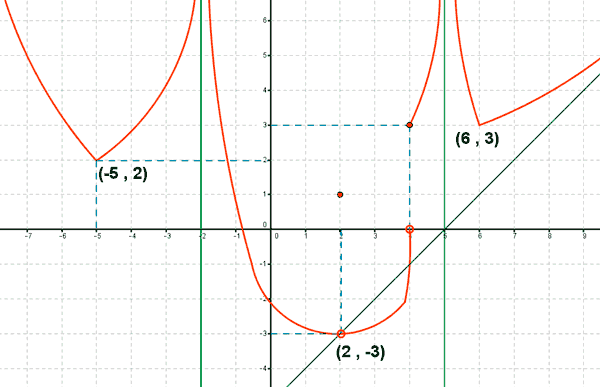
a) Dominio.
La función no está definida en los puntos: x = -2 , x = 5
Dom(f) = R - {-2 , 5}
b) Recorrido.
Observamos que la gráfica se mueve en eje de ordenadas en el intervalo: (-3 , ∞)
Im(f) = (-3 , ∞)
c) Extremos absolutos y relativos.
Extremos absolutos:
La función no está acotada superiormente.
La función está acotada inferiormente por k = -3, además es la mayor de las cotas inferiores, por tanto es un ínfimo de la función inf(f) = -3. Sin embargo, no llega a alcanzar este punto, por lo que no podemos decir que sea un mínimo absoluto de la función.
Extremos relativos:
No tiene máximos relativos.
Tiene dos mínimos relativos en: (-5 , 2) , (6 , 3)
d) Discontinuidades y su clasificación.
En x = -2 la función tiene una discontinuidad de primera especie o de salto infinito. Lo mismo ocurre con x = 5 . Se comprueba estudiando los límites laterales:
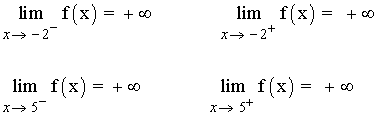
En x = 2 tiene un punto de discontinuidad evitable:
f(2) = 1
![]()
En x = 4 tiene una discontinuidad de primera especie o de salto finito:
![]()
e) Asíntotas.
Asíntotas verticales: x = - 2 , x = 5
Asíntotas horizontales:
![]()
No tiene asíntotas horizontales.
Asíntota oblícua:
Si y = 0 ⇒ x = 5
La asíntota oblicua es: y = x - 5
Estudiar la siguiente gráfica:
a) Dominio.
b) Recorrido.
c) Extremos absolutos y relativos.
d) Discontinuidades y su clasificación.
e) Asíntotas.
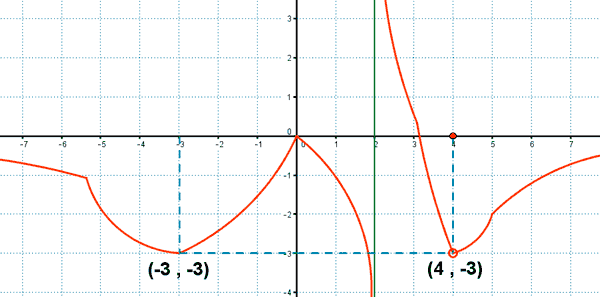
a) Dominio.
La función no está definida en el punto: x = 2
Dom(f) = R - {2} = (-∞ , 2) ∪ (2 , ∞)
b) Recorrido.
Observamos que la gráfica se mueve a lo largo de todo el eje de ordenadas.
Im(f) = R
c) Extremos absolutos y relativos.
Extremos absolutos:
La función no está acotada ni superior ni inferiormente, por lo que no tiene ni máximos ni mínimos absolutos.
Extremos relativos:
La función tiene un máximo relativo en: (0 , 0)
La función tiene un mínimo relativo en: (-3 , -3)
d) Discontinuidades y su clasificación.
En x = 2 la función tiene una discontinuidad de primera especie o de salto infinito:
![]()
En x = 4 :
f(4) = 0
![]()
Es una discontinuidad evitable.
e) Asíntotas.
Asíntotas verticales: x = 2
Asíntotas horizontales:
![]()
Tiene una asíntota horizontal en: y = 0
Asíntota oblícua: como tiene asíntota horizontal, no puede tener asíntota oblicua.
Estudia el dominio y la discontinuidad de las siguientes funciones:
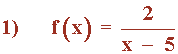
Para ver su dominio calculamos los puntos que anulan al denominador: x - 5 = 0 ⇔ x = 5
Dom(f) = R - {5}
Veamos que tipo de discontinuidad es x = 5 :
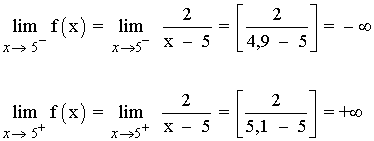
Como f(5) no existe y los límites laterales dan ±∞ , la función f tiene una discontinuidad de primera especie o de salto infinito en x = 5 .
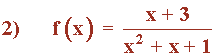
Para ver su dominio calculamos los puntos que anulan al denominador:
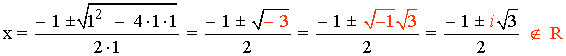
Los valores que anulan el denominador son complejos, por tanto, la función está bien definida para todo número real.
Luego: Dom(f) = R
La función es continua en toda la recta real, por tanto, no tiene puntos de discontinuidad.
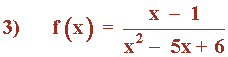
Para ver su dominio calculamos los puntos que anulan el denominador:
x2 - 5x + 6 = 0 ⇔ x = 3 , x = 2
Luego: Dom(f) = R - {2 , 3}
Veamos que tipo de discontinuidad son:
x = 2
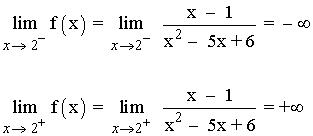
Como f(2) no existe y los límites laterales dan ∞ , la función f tiene una discontinuidad de primera especie o de salto infinito.
x = 3
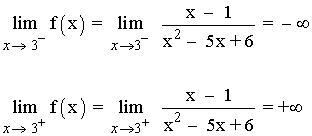
Como f(3) no existe y los límites laterales dan ∞ , la función f tiene una discontinuidad de primera especie o de salto infinito.
SELECTIVIDAD
Estudiar la continuidad de la función
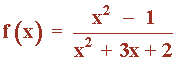
y clasificar sus diferentes tipos de discontinuidad.
Veamos cuáles son los puntos que anulan el denominador:
x2 + 3x + 2 = 0 ⇔ x = - 2 , x = - 1
Estudiemos la continuidad en dichos puntos:
x = -2
f(-2) no existe
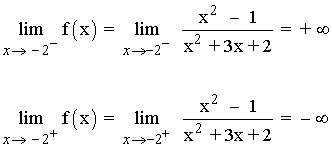
Como f(-2) no existe y los límites laterales dan ∞ , la función f tiene una discontinuidad de primera especie o de salto infinito en el punto x = -2 .
x = -1
f(-1) no existe
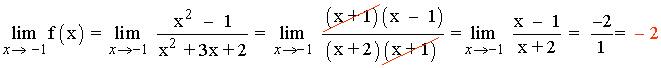
Como f(-1) no existe y el límite cuando x → -1 es finito (igual a -2) , la función f tiene una discontinuidad evitable en el punto x = - 2 .
Por tanto, la función es continua en R - {-2 , -1} .
SELECTIVIDAD
Estudiar la continuidad de la función
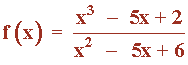
clasificando las discontinuidades que se encuentren. ¿Es posible definir de nuevo la función para evitar alguna discontinuidad?
Veamos cuáles son los puntos que anulan el denominador:
x2 - 5x + 6 = 0 ⇔ x = 2 , x = 3
Estudiemos la continuidad en dichos puntos:
x = 2
f(2) no existe
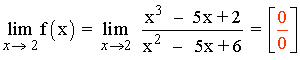
Para resolver la indeterminación factorizamos numerador y denominador:
x2 - 5x + 6 = (x - 2)(x - 3)
Factorizamos el numerador por Ruffini probando primero con alguna de las raíces del denominador:
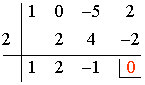
x3 - 5x + 2 = (x - 2)(x2 + 2x - 1)
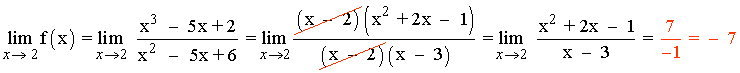
Como f(2) no existe y el límite cuando x → 2 es finito (igual a -7) , la función f tiene una discontinuidad evitable en el punto x = 2 .
x = 3
f(3) no existe
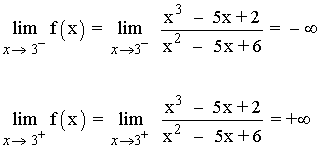
Como f(3) no existe y los límites laterales dan ∞ , la función f tiene una discontinuidad de primera especie o de salto infinito en x = 3 .
Por tanto, la función es continua en R - {2 , 3} .
Como en x = 2 la discontinuidad es evitable, podemos redefinir la función f para que sea continua en dicho punto.
Para ello, definimos f en x = 2 como el resultado del límite de f cuando x → 2 :
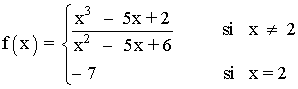
Estudia el dominio y la discontinuidad de las siguientes funciones:
![]()
Para ver su dominio calculamos los puntos que hacen positivo el argumento de la raíz: 5 - x ≥ 0 ⇔ x ≥ 5
Dom(f) = [5 , ∞)
La función es continua en todos los puntos de su dominio, es decir, es continua en el intervalo [5 ,∞) . Por tanto, no tiene puntos de discontinuidad.
![]()
Para ver su dominio calculamos los puntos que hacen positivo los argumentos de cada raíz:
3 + x ≥ 0 y 3 - x ≥ 0
Resolvemos el sistema de inecuaciones:
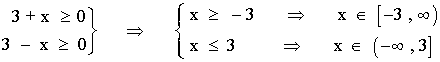
Dom(f) = (-∞ , -3] ∩ [3 , ∞) = [-3 , 3]
La función es continua en todos los puntos de su dominio, es decir, es continua en el intervalo [-3 , 3] . Por tanto, no tiene puntos de discontinuidad.
![]()
Para ver su dominio calculamos los puntos que hacen positivo el argumento de la raíz:
3 - 2x - x2 = 0 ⇔ x = 1 , x = -3
3 - 2x - x2 = - (x - 1)(x + 3) ≥ 0
Estudiamos el signo en los intervalos: (-∞ -3) , (-3 , 1) , (1 , ∞)
• (-∞ , -3) : x = -4 ⇒ - (-4 - 1)(-4 + 3) < 0
• (-3 , 1) : x = 0 ⇒ - (0 - 1)(0 + 3) > 0
• (1 , ∞) : x = 2 ⇒ - (2 - 1)(2 + 3) < 0
Por tanto: 3 - 2x - x2 ≥ 0 ⇔ x ∈ [- 3 , 1]
Dom(f) = [-3 , 1]
La función es continua en todos los puntos de su dominio, es decir, es continua en el intervalo [-3 , 1] . Por tanto, no tiene puntos de discontinuidad.
![]()
Para ver su dominio calculamos los puntos que hacen positivo el argumento de la raíz:
x2 - 6x + 9 = 0 ⇔ x = 3
x2 - 6x + 9 = (x - 3)2 ≥ 0
El argumento de la raíz siempre es mayor o igual que 0.
Por tanto, la función f está bien definida en toda la recta real.
Dom(f) = R
Es continua en todos los puntos de su dominio, por lo que no tiene puntos de discontinuidad.
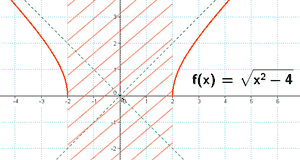
Estudia la continuidad de la siguiente función y dibújala:
![]()
Hallamos el dominio de la función:
![]()
Estudiamos el signo en los intervalos: ( -∞ , -2) , (-2 , 2) , (2 , ∞)
• (-∞ , - 2): x = - 3 ⇒ (x + 2)(x - 2) = (- 3 + 2)(- 3 - 2) = 5 > 0
• (-2 , 2): x = 0 ⇒ (x + 2)(x - 2) = 2 · (-2) = -4 < 0
• (2 , ∞): x = 3 ⇒ (x + 2)(x - 2) = (3 + 2)(3 - 2) = 5 > 0
Por tanto: Dom f = (-∞ , -2) ∪ (2 , ∞)
Por tanto tenemos que estudiar la continuidad de la función en los puntos: x = 2 , x = - 2
f(2) = 0
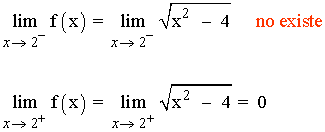
La función f tiene una discontinuidad de segunda especie o asintótica en el punto x = 2 .
f(-2) = 0
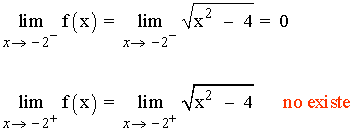
La función f tiene una discontinuidad de segunda especie o asintótica en el punto x = -2 .
Por tanto, la función es continua en: (-∞ , -2) ∪ (2 , ∞)
Estudia el dominio y la discontinuidad de las siguientes funciones:
![]()
Para ver su dominio calculamos los puntos que hacen estrictamente positivo el argumento del logaritmo:
x2 - 4 > 0 ⇔ x2 > 4 ⇔ |x| >√4 ⇔ |x| >2 ⇔ x < -2 y x > 2 ⇔ x ∈ (-∞ , -2) ∪ (2 , ∞)
Dom(f) = (-∞ , -2) ∪ (2 , ∞)
Es continua en todos los puntos de su dominio, es decir, es continua en (-∞ , -2) ∪ (2 , ∞) . Por tanto, la función no tiene puntos de discontinuidad.
SELECTIVIDAD
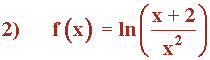
El argumento del logaritmo es racional. El único punto que anula su denominador es x = 0 .
Veamos ahora para qué puntos el argumento del logaritmo es estrictamente positivo:
![]()
También se tiene que cumplir: x ≠ 0
Dom(f) = (-2 , ∞) - {0} = (-2 , 0) ∪ (0 , ∞)
Es continua en todos los puntos de su dominio, es decir, es continua en (-2 , 0) ∪ (0 , ∞) . Por tanto, la función no tiene puntos de discontinuidad.


 INICIO
INICIO