Problemas y ejercicios de límites y continuidad con parámetros
Calcula la incógnita a para que se cumpla que:
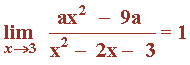
Observamos que x=3 es raíz tanto del numerador como del denominador, lo que nos da una indeterminación:
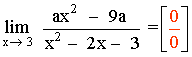
Como x=3 es raíz del denominador lo factorizamos mediante Ruffini.
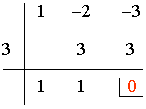
Luego: x2 - 2x - 3 = (x - 3)(x + 1)
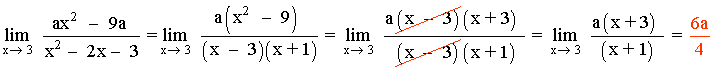
Como el límite tiene que dar 1 , lo igualamos con nuestro resultado:
![]()
SELECTIVIDAD
Determinar a para que se verifique:
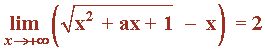
Vamos a intentar resolver el límite como si no hubiese parámetro. Para ello, multiplicamos y dividimos por la conjugada de la expresión:
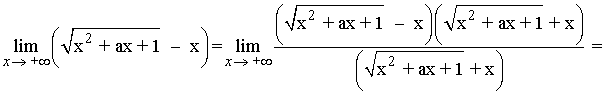
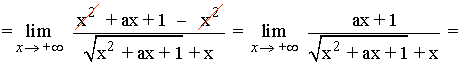
Dividimos numerador y denominador por x (el argumento de la raíz se divide por x2):
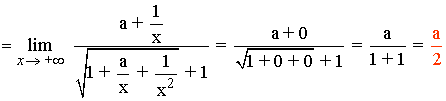
El enunciado exige que el resultado del límite sea 2, por tanto:
![]()
Calcula la incógnita a para que se cumpla que:
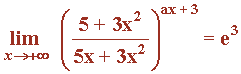
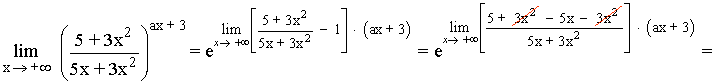
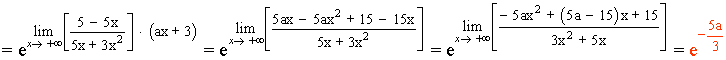
Como el límite tiene que dar e3 , lo igualamos con nuestro resultado:

SELECTIVIDAD
La siguiente función presenta una discontinuidad evitable en x = -2 , ¿para qué valor de a ?
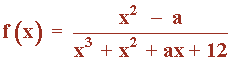
Para que la discontinuidad en x = -2 sea evitable, el límite cuando x → -2 tiene que ser una indeterminación del tipo: 0/0
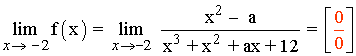
Exigiendo que los límites del numerador y del denominador cuando x → -2 tienen que ser 0 obtenemos:
![]()
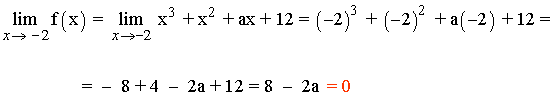
8 - 2a = 0 ⇔ 8 = 2a ⇔ a = 4
Vamos a comprobar que para a = 4 se tiene la discontinuidad evitable que buscamos.
Factorizamos el numerador y el denominador:
x2 - 4 = (x - 2)(x + 2)
Sabemos que el denominador se anula en x = -2:
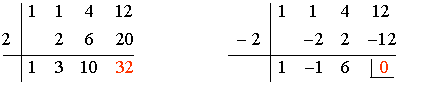
x3 + x2 + ax + 12 = (x + 2)(x2 - x + 6)
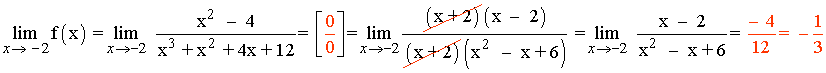
Como f(-2) no existe y el límite cuando x → -2 es finito (igual a -1/3) la función f tiene una discontinuidad de primera especie o de salto finito en x = -2 .
Como es de salto finito, se trata de una discontinuidad evitable.
Hallar el valor de k para que la función f(x) sea continua en x = 1 :
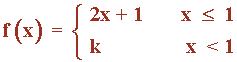
Las funciones que definen a f son continuas para cualquier valor de k.
El único punto en el que puede haber problema es en el de abscisa: x = 1
f(1) = 2·1 + 1 = 3
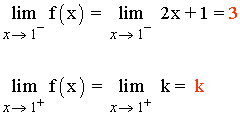
Para que el límite cuando x → 1 exista, los límites laterales tienen que coincidir:
![]()
Luego:
![]()
Y observamos que:
![]()
La función f es continua en x = 1 .
Calcular el valor de a para que f(x) sea continua en toda la recta real:
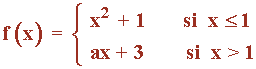
Las funciones que definen f son polinómicas, por tanto, son continuas en todo R .
El único punto en el que puede haber problema es en el de abscisa: x = 1
f(1) = 12 + 1 = 2
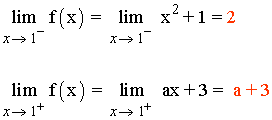
Para que el límite cuando x → 1 exista, los límites laterales tienen que coincidir:
![]()
Para que la función f sea continua en x = 1 se tiene que cumplir:
![]()
Si a = -1 la función f es continua en todo punto de la recta real.
Hallar los valores de a y b para que la función f(x) sea continua en todos los números reales:
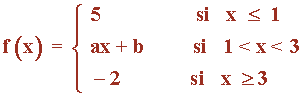
Las funciones que definen a f son continuas en todos los números reales para cualquier valor de a y b.
Los únicos puntos en los que puede haber problema son en los de abscisa: x = 1 , x = 3
x = 1
f(1) = 5
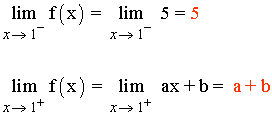
Para que el límite cuando x → 1 exista, los límites laterales tienen que coincidir:
![]()
Para que la función f sea continua en x = 1 se tiene que cumplir:
![]()
x = 3
f(3) = - 2
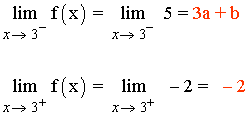
Para que el límite cuando x → 3 exista, los límites laterales tienen que coincidir:
![]()
Para que la función f sea continua en x = 3 se tiene que cumplir:
![]()
Reuniendo ambas ecuaciones tenemos un sistema de dos ecuaciones con dos incógnitas:
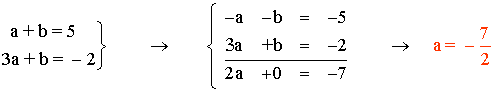
![]()
Si a = -7/2 y b = 17/2 se cumplen ambas condiciones de continuidad, y entonces, la función f es continua en todo R .
SELECTIVIDAD
Halla el valor de k para que la siguiente función sea continua en todo punto:
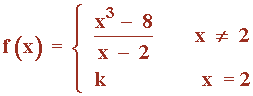
Para x≠2 la función está definida como una función racional, la cual no esta definida para el valor que anula el denominador: x = 2
Por tanto, para cualquier valor de k la función f es continua en todo punto menos en x = 2 .
Para que la función sea continua en x = 2 se tiene que cumplir la condición de continuidad:
![]()
f(2) = k
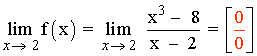
Para resolver el límite factorizamos el numerador mediante Ruffini:
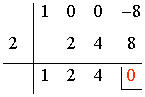
p(x) = x3 - 8 = (x - 2)(x2 + 2x + 4)
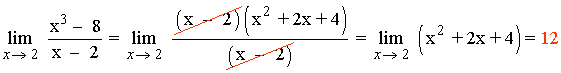
Imponiendo la condición de continuidad en x = 2 obtenemos:
![]()
Luego la función f es continua en todo punto si, y sólo si, k = 12 .
SELECTIVIDAD
Calcula los valores de a,b ∈ R para que la siguiente función sea continua en todo punto.
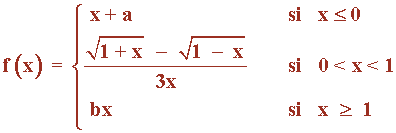
Veamos primero la continuidad de cada rama de la función:
• f(x) = x + a es una función polinómica, por lo que es continua en todo R, y en particular es continua en su intervalo de definición: (-∞ , 0]
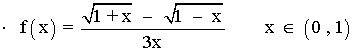
El único valor que anula al denominador es x = 0 , pero no pertenece al intervalo de definición de esta rama: x=0 ∉ (0 , 1)
Por tanto, f(x) es continua en (0 , 1) .
• f(x) = bx es una función polinómica, por lo que es continua en todo R, y en particular es continua en su intervalo de definición: [1 , ∞)
Estudiamos la continuidad en los puntos de unión de las ramas da la función: x = 0 , x = 1
x = 0
Para que f sea continua en x = 0 se tiene que cumplir:
![]()
f(0) = a
![]()
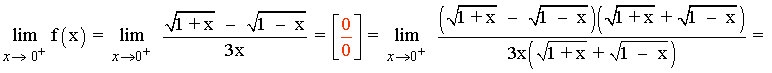
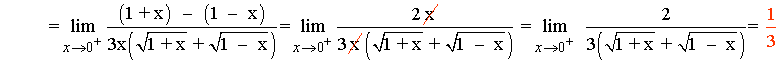
Para que el límite cuando x → 0 exista los límites laterales tienen que coincidir:
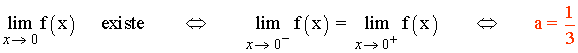
Luego si a = 1/3 la función f es continua en x = 0 :
![]()
x = 1
Para que f sea continua en x = 0 se tiene que cumplir:
![]()
f(1) = b
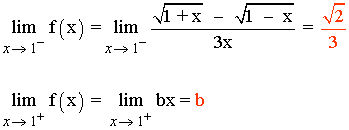
Para que el límite cuando x → 0 exista los límites laterales tienen que coincidir:
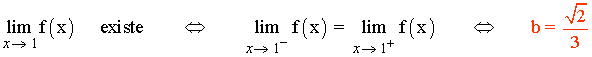
Luego si b = √2/3 la función f es continua en x = 1 :
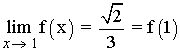
Por tanto, si a = 1/3 y b = √2/3 la función f es continua en todo R .
SELECTIVIDAD
Considera la función f: (-∞ , 10) → R definida por:
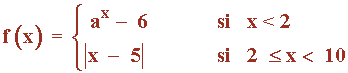
a) Determina el valor de a sabiendo que f es continua (y que a > 0).
b) Esboza la gráfica de f.
a) Determina el valor de a sabiendo que f es continua (y que a > 0).
Reescribimos la función:
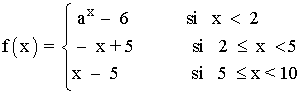
Las funciones que definen f son continuas en todo R , y en particular lo son en sus respectivos intervalos de definición.
Como nos afirman que la función f es continua, en particular lo es en los puntos de unión: x = 2 , x = 5
En cada caso se tiene que cumplir:
![]()
x = 2
f(2) = - 2 + 5 = 3
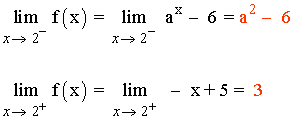
Para que el límite cuando x → 2 exista los límites laterales tienen que coincidir:
![]()
Si a = 3 > 0 se cumple la condición de continuidad:
![]()
x = 5
f(5) = 5 - 5 = 0
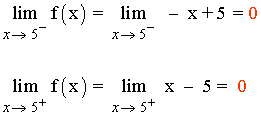
Como los límites laterales coinciden, el límite cuando x → 5 existe y vale:
![]()
Por tanto, para que la función sea continua en (-∞ , 10) tiene que ser a = 3 .
b) Esboza la gráfica de f.
Hallamos los puntos de corte con los ejes:
• Si x = 0 : y = f(0) = 30 - 6 = 1 - 6 = - 5 ⇒ (0 , -5)
• Si y = 0 : 3x - 6 = 0 3x = 6 ⇒ log3 6 = x ⇒ (log3 6 , 0)
- x + 5 = 0 ⇒ x = 5 ⇒ (5 , 0)
x - 5 = 0 ⇒ x = 5 ⇒ (5 , 0)
Como la función es continua en los puntos de unión, podemos hallar dichos puntos:
• x = 2 : f(2) = - 2 + 5 = 3 ⇒ (2 , 3)
• x = 5 : f(5) = 5 - 5 = 0 ⇒ (5 , 0)
La función f no tiene asíntotas verticales. Veamos si tiene horizontales:
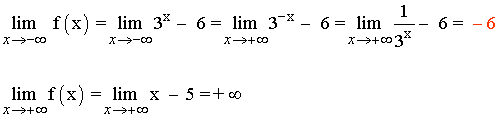
Hay una asíntota horizontal en y = -6.
Como hay asíntota horizontal, no hay oblicua.
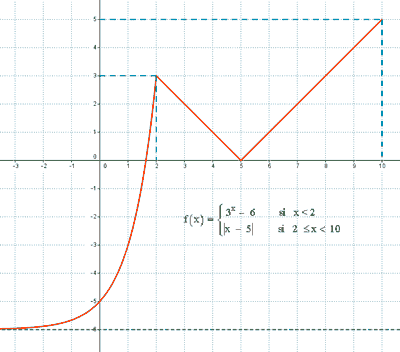
SELECTIVIDAD
Sea f: R → R la función continua definida por:
donde a es un número real. Determina a .
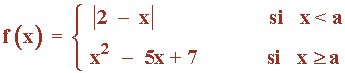
Las funciones que definen a f son funciones continuas en todo R , en particular, en sus respectivos intervalos de definición.
Tenemos que estudiar la continuidad en el punto de unión. Según el valor de a , la función f se define:
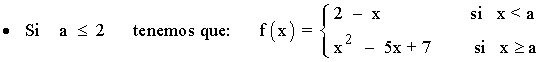
f(a) = a2 - 5a + 7
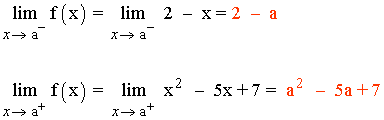
Para que el límite cuando x → a exista los límites laterales tienen que coincidir:
![]()
Por tanto, si a ≤ 2 la función no puede ser continua en a .
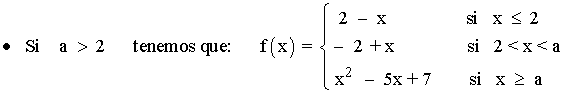
Tenemos que estudiar la continuidad en los puntos: x = 2 , x = a
x = 2
f(2) = 2 - 2 = 0
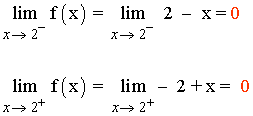
Como los límites laterales coinciden, el límite cuando x → 2 existe y vale:
![]()
Luego la función f es continua en x = 2 .
x = a
f(a) = a2 - 5a + 7
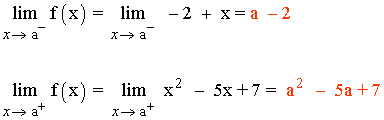
Para que el límite cuando x → a exista los límites laterales tienen que coincidir:
![]()
Si a = 3 los límites laterales coinciden, y por tanto, el límite cuando x → a existe y vale:
![]()
Luego la función f es continua en x = a .
Conclusión:
• Si a ≤ 2 : la función es continua en (-∞ , a) ∪ (a , ∞)
• Si a > 2 : la función es continua en todo R .
SELECTIVIDAD
Hallar el valor de los parámetros a y b de modo que la siguiente función sea continua.
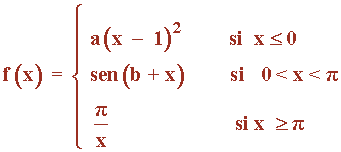
Las funciones que definen a f son funciones continuas en todo R .
Los únicos valores en los que puede haber problema son en los de abscisa: x = 0 , x = π
x = 0
f(0) = a
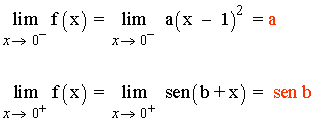
Para que el límite cuando x → 1 exista, los límites laterales tienen que coincidir:
![]()
x = π
f(π) = π/π = 1
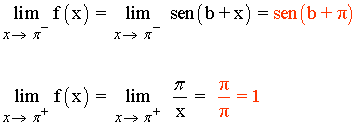
Para que el límite cuando x → π exista, los límites laterales tienen que coincidir:
![]()
Reuniendo ambas ecuaciones tenemos un sistema de dos ecuaciones con dos incógnitas:
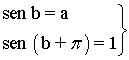
![]()
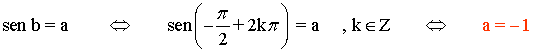
Hallar los valores de a y b para que la siguiente función sea continua en todo número real x .
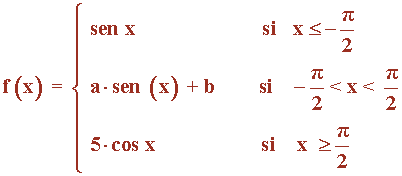
Las funciones que definen a f son funciones continuas en todo R .
Los únicos valores en los que puede haber problema son en los de abscisa: x = -π/2 , x = π/2
x = -π/2
f(-π/2) = - 1
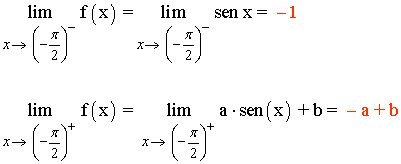
Para que el límite cuando x → -π/2 exista, los límites laterales tienen que coincidir:
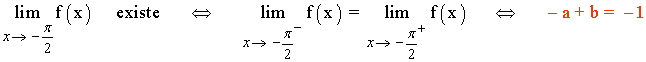
x = π/2
f(π/2) = 0
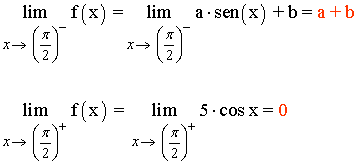
Para que el límite cuando x →π/2 exista, los límites laterales tienen que coincidir:
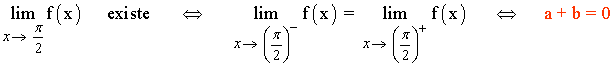
Reuniendo ambas ecuaciones tenemos un sistema de dos ecuaciones con dos incógnitas:
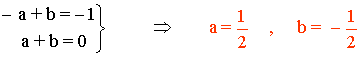
SELECTIVIDAD
¿Qué valor debe tomar a en la siguiente función para que sea continua en el punto x = 4 ?
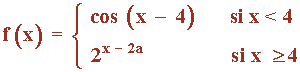
La función será continua en x = 4 si se cumple que:
![]()
f(4) = 24 - 2a
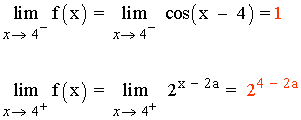
Para que el límite cuando x → 4 exista, los límites laterales tienen que coincidir:
![]()
24 - 2a = 1 ⇔ 24 - 2a = 20 ⇔ 4 - 2a = 0 ⇔ 4 = 2a ⇔ a = 2
Si a = 2 se cumple:
![]()
Luego si a = 2 la función f es continua en el punto x = 4 .


 INICIO
INICIO