Teorema de Rouché-Frobënius:
Discusión de las soluciones de los sistemas de ecuaciones lineales
Teorema de Rouché-Frobënius
Considerando el sistema general de m ecuaciones y n incógnitas
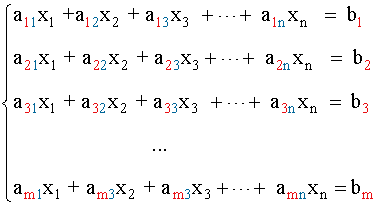
Podemos considerar las matrices A y A'
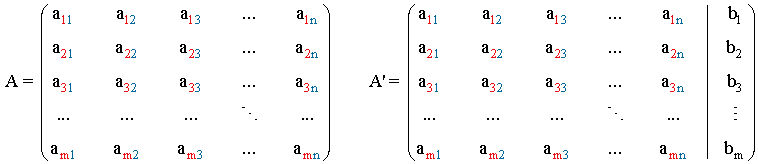
donde A es la matriz de coeficientes del sistema y A' es la matriz ampliada del sistema.
Teorema de Rouché-Fröbenius
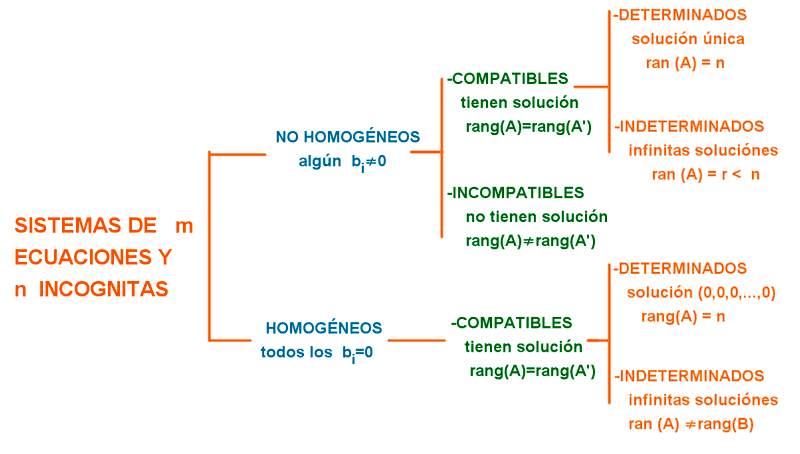
- rg (A) = rg(A') = n ⇒ El sistema es compatible determinado (solución única).
- rg (A) = rg(A') < n ⇒ El sistema es compatible indeterminado (infinitas soluciones).
- rg (A) ≠ rg(A') ⇒ El sistema es incompatible (no tiene solución).
Ejemplo de discusión de sistema de dos ecuaciones con dos incógnitas
utilizando el teorema de Rouché-Frobënius
1.- Discutir el siguiente sistema de ecuaciones
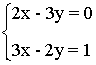
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
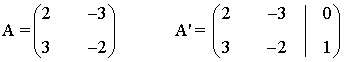
Para este sistema n = 2. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 2 ya que A es una matriz cuadrada de orden 2 y A' es una matriz 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Vemos que |A| = 5 ≠ 0 de manera que rg(A) = 2 y como |A| es un menor de orden 2 de la matriz A', también rg(A ') = 2.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto rg(A) = rg(A') = 2 y el sistema es compatible determinado.
Ejemplo de discusión de sistema de tres ecuaciones con dos incógnitas
utilizando el teorema de Rouché-Frobënius
1.- Discutir el siguiente sistema de ecuaciones
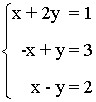
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
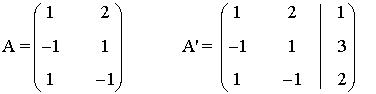
Para este sistema n = 2. Observamos que tanto el rango de A puede ser a lo sumo 2 ya que A es una
matriz es una matriz 3 × 2, mientras que el rango de A' puede ser a lo sumo 3, ya que A' es una matriz
de orden 3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A'.
Vemos que
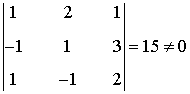
de manera que rg(A') = 3.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto, como rg(A) ≤ 2 y rg(A') = 3, rg(A) ≠ rg(A') y el sistema es incompatible.
Ejemplos de discusión de sistemas de tres ecuaciones con tres incógnitas
utilizando el teorema de Rouché-Frobënius
1.- Discutir el siguiente sistema de ecuaciones
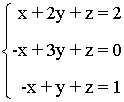
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
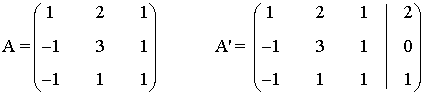
Para este sistema n = 3. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 3 ya que A es una matriz cuadrada de orden 3 y A' es una matriz 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Vemos que |A| = 4 ≠ 0 de manera que rg(A) = 3 y como |A| es un menor de orden 3 de la matriz A',
también rg(A ') = 3.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto rg(A) = rg(A') = 3 y el sistema es compatible determinado.
2.- Discutir el siguiente sistema de ecuaciones
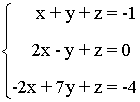
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
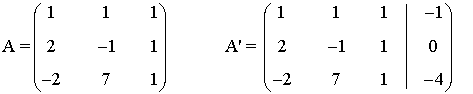
Para este sistema n = 3. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 3 ya que A es una matriz cuadrada de orden 3 y A' es una matriz 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A.
Vemos que
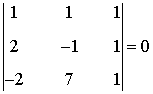
de manera que rg(A) < 3. Observamos que
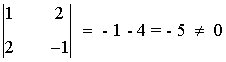
es decir, A tiene un menor de orden 2 no nulo, de manera que rg(A) = 2.
Dicho menor es también un menor de orden 2 de A', por lo cual rg(A') ≥ 2. El menor puede orlarse de
dos formas:
Añadiendo la última fila y la tercera columna, lo cual da lugar a |A|, que hemos visto que se anula.
Añadiendo la última fila y la última columna de A':
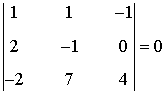
Como los menores orlados son ambos nulos rg(A') = 2.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto rg(A) = rg(A') = 2 < 3 y el sistema es compatible indeterminado.
3.- Discutir el siguiente sistema de ecuaciones
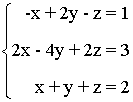
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
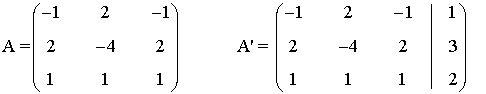
Para este sistema n = 3. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 3 ya que A es una matriz cuadrada de orden 3 y A' es una matriz 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A.
Vemos que
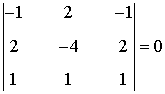
de manera que rg(A) < 3. Observamos que
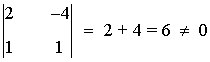
es decir, A tiene un menor de orden 2 no nulo, de manera que rg(A) = 2.
Dicho menor es también un menor de orden 2 de A', por lo cual rg(A') ≥ 2. El menor puede orlarse de
dos formas:
Añadiendo la primera fila y la tercera columna, lo cual da lugar a |A|, que hemos visto que se anula.
Añadiendo la primera fila y la última columna de A':
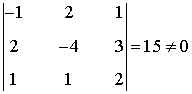
Como este menor es no nulo, tenemos que rg(A') = 3.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto, como rg(A)=2 y rg(A')=3, rg(A) ≠ rg(A') y el sistema es incompatible.
Ejemplo de discusión de sistema de dos ecuaciones con tres incógnitas
utilizando el teorema de Rouché-Frobënius
1.- Discutir el siguiente sistema de ecuaciones
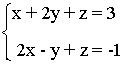
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
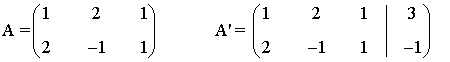
Para este sistema n = 3. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 2 ya que A es una matriz 2 × 3 y A' es una matriz 2 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Estudiamos los rangos de A y de A'.
Vemos que
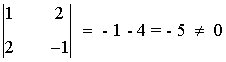
de manera que rg(A) = 2. Dicho menor es también un menor de A'. Por tanto rg(A') = 2
El rango de la matriz es el orden del mayor menor no nulo
Por tanto rg(A) = rg(A') = 2 < 3 y el sistema es compatible indeterminado.
Ejemplo de discusión de sistema de tres ecuaciones con cuatro incógnitas
utilizando el teorema de Rouché-Frobënius
1.- Discutir el siguiente sistema de ecuaciones
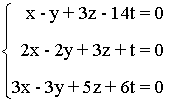
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
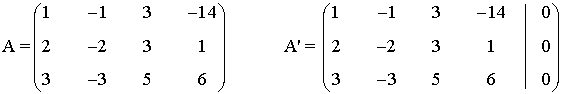
Para este sistema n = 4. Observamos que tanto el rango de A como el rango de A' pueden ser a lo
sumo 3 ya que A es una matriz 3 × 4 y A' es una matriz 3 × 5.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A.
Vemos que
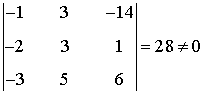
de manera que rg(A) = 3. Como dicho menor también es un menor de A' entonces rg(A') = 3.
Por tanto rg(A) = rg(A') = 3 < 4 y el sistema es compatible indeterminado.
Número de ecuaciones y número de incógnitas
Nº de ecuaciones < Nº de incógnitas
- No puede ser compatible determinado.
- Puede ser incompatible (basta que haya dos ecuaciones contradictorias).
Nº de ecuaciones = Nº de incógnitas + 1
- Es un sistema que tiene una ecuación más que incógnitas.
- Para discutir el sistema se calcula primero |A'|.
- Si |A'| ≠ 0 sistema incompatible.
Nº de ecuaciones = Nº de incógnitas
- Para discutir el sistema se calcula primero |A|.
- Si |A'| ≠ 0 sistema compatible determinado.
- Si |A| = 0 hay que estudiar el rango de A'.


 INICIO
INICIO

