Ejercicios resueltos de discusión de sistemas con parámetros
por el teorema de Rouché - Fröbenius
1. Discute en función de a el sistema
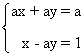
2. Averigüe si el siguiente sistema puede ser compatible indeterminado
para algún valor de m
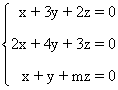
¿Es incompatible para algún valor de m?
3. Discutir la compatibilidad del siguiente sistema de ecuaciones en función del parámetro a.
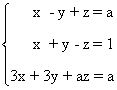
4. Discute el sistema de ecuaciones lineales según los valores de b.
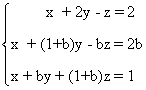
5. Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible
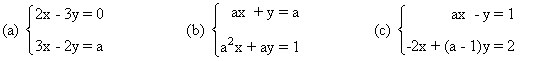
6. Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible
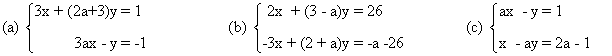
7. Discute y resuelve, según los valores del parámetro, los siguientes sistemas de ecuaciones:
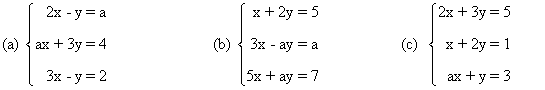
8 . Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible.
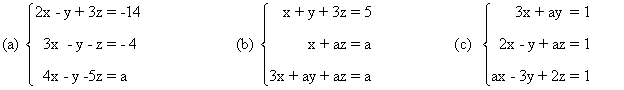
9 . Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible.
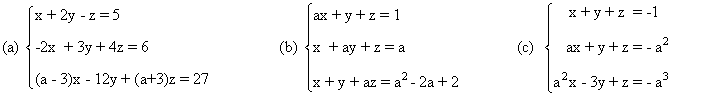
10 . Estudia los siguientes sistemas homogéneos según los valores del parámetro a y resuélvelos en los casos en que sea posible.

11 . Estudia los siguientes sistemas homogéneos según los valores del parámetro a y resuélvelos en los casos en que sea posible.

12 . Discute y resuelve, según los valores del parámetro, los siguientes sistemas:

13 . Discute y resuelve, según los valores del parámetro, los siguientes sistemas:

14 .) Cuadro resumen de Rouché
1. Discute en función de a el sistema
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
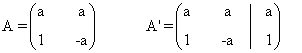
Para este sistema el número de incógnitas es 2, es decir n = 2. Observamos que el rango de A puede
ser a lo sumo 2, ya que A es una matriz de orden 2. También el rango de A' es a lo sumo 2 ya que A' es una matriz 2 × 3
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Las matrices A y A' tienen orden al menos 1 ya que |1| es un menor no nulo de orden 1. Veamos qué ocurre con orlados de |1|
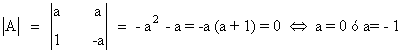
Con esto acabamos de obtener que si a ≠ 0 y a ≠ -1 entonces rg(A) = rg(A') = 2.
Veamos ahora qué ocurre si a = 0 ó a = -1. En estos casos ya sabemos que rg(A) = 1, de manera que habría que estudiar el otro orlado de |1| para determinar el rango de A' :
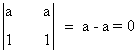
Como dicho menor se anula para todo a, en particular también lo hace para a = 0 y a = -1 y
rg(A') = 1.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto,

2. Averigüe si el siguiente sistema puede ser compatible indeterminado
para algún valor de m
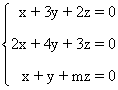
¿Es incompatible para algún valor de m?
Empezamos resolviendo primero la última cuestión. La respuesta es negativa. Como el sistema es homogéneo sabemos que siempre es compatible, ya que siempre tiene, como solución al menos a la solución trivial.
Observamos que en este caso n = 3 ya que hay tres incógnitas. Empezamos escribiendo la matriz de coeficientes del sistema:
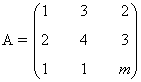
Estudiamos su rango:
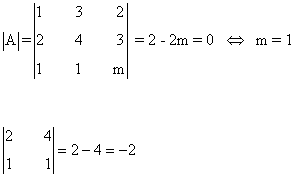
Vemos que

La respuesta a la pregunta que planteaba el problema es afirmativa. Si m = 1, el sistema es compatible indeterminado.
3. Discutir la compatibilidad del siguiente sistema de ecuaciones en función del parámetro a.
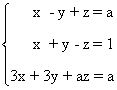
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
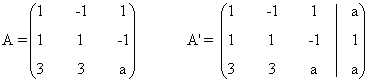
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
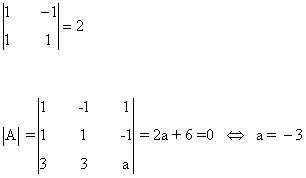
por lo cual
si a ≠ -3 entonces rg(A)=rg(A') = 3 y
si a = -3 entonces rg(A) = 2 y tenemos que estudiar el rango de A'. Calculando el otro menor orlado
de orden 3 para a = -3 obtenemos que
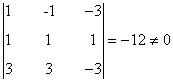
de manera que rg(A')=3.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto,
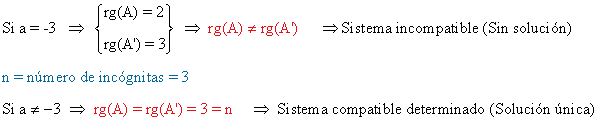
4. Discute el sistema de ecuaciones lineales según los valores de b.
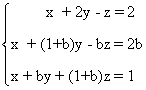
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
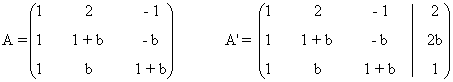
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
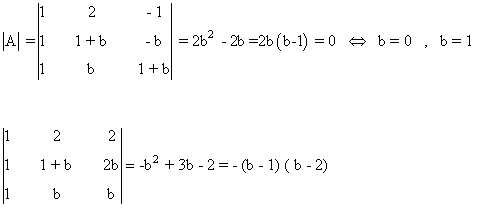
por lo cual
- si b ≠ 0 y b ≠ 1 entonces rg(A) = rg(A') = 3.
- si b = 0,
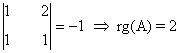
y el otro menor de orden 3 es no nulo, de manera que rg(A') = 3 - si b = 1,
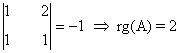
y el otro menor de orden 3 es nulo, de manera que rg(A') = 2.
El rango de la matriz es el orden del mayor menor no nulo
Por tanto,

5. Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible
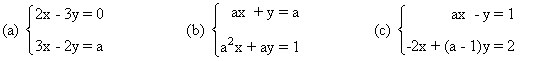
(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
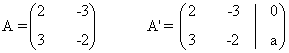
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que |A| = -4 + 9 = 5 ≠ 0, de manera que rg(A) = rg(A') = 2 = n y el sistema es
compatible determinado para cualquier valor de a. Resolvemos ahora por el método de Cramer:

(b)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
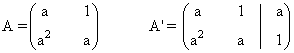
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que |A| = a2 - a2 = 0, de manera que rg(A) =1 para todo a.
Por otra parte
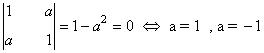
de manera que
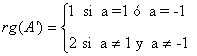
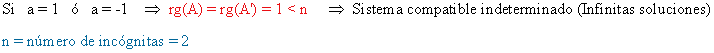
En estos casos las soluciones son:
- Si a = 1:
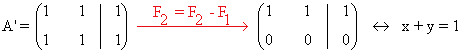
de manera que basta resolver el sistema equivalente x + y = 1. Para ello se considera y = λ
y de manera que las soluciones son:x = 1 - λ y = λ
- Si a = -1:
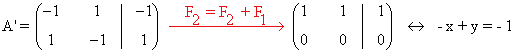
de manera que basta resolver el sistema equivalente -x + y = -1. Para ello se considera y = λ
de manera que las soluciones son:x = 1 + λ y = λ
Finalmente 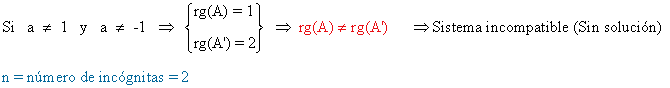
(c)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
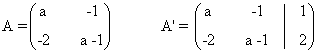
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que |A| = a2 - a2 -2 = 0 si y sólo si a = -1 ó a = 2, de manera que rg(A) =2 para
todo a distinto de -1 y de 2.
Por otra parte
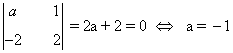
de manera que
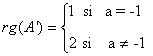
Sabido esto ya podemos discutir y resolver el sistema en función de a:
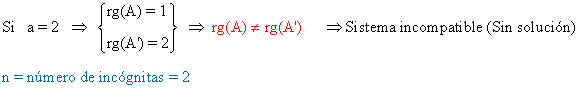

y obtenemos que
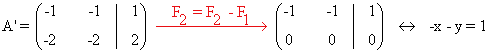
de manera que basta resolver el sistema equivalente -x - y = 1. Para ello se considera y = λ
y de manera que las soluciones son:
x = -1 - λ y = λ
Finalmente
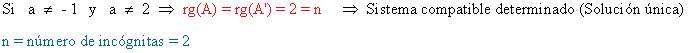
Resolvemos el sistema por el método de Cramer:

6. Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible
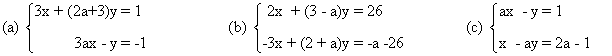
(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
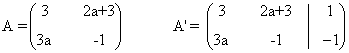
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
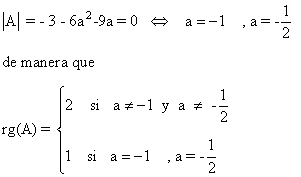
Por otra parte
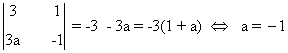
de manera que
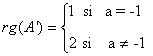
Sabido esto ya podemos discutir y resolver el sistema en función de a:
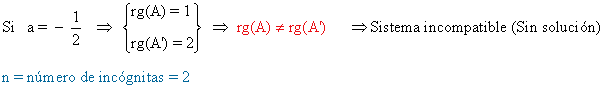

y obtenemos que
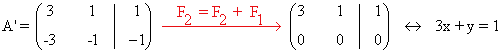
de manera que basta resolver el sistema equivalente 3x + y = 1. Para ello se considera y = λ
y de manera que las soluciones son:
![]()
Finalmente
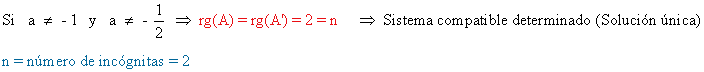
Resolvemos el sistema por el método de Cramer:

(b)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
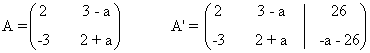
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
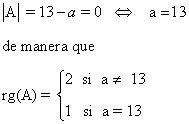
Por otra parte
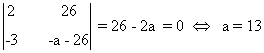
de manera que
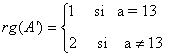
Sabido esto ya podemos discutir y resolver el sistema en función de a:

y obtenemos que
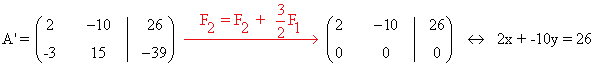
de manera que basta resolver el sistema equivalente 2x -10y = 26. Para ello se considera y = λ
y de manera que las soluciones son:
![]()
Finalmente

Resolvemos el sistema por el método de Cramer:
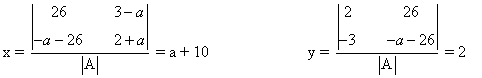
(c)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
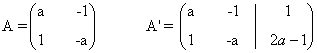
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 2. También el rango de A' puede ser a lo sumo 2, ya
que A' es una matriz
de orden 2 ×3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
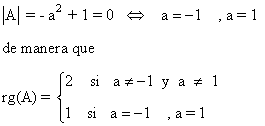
Por otra parte
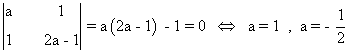
de manera que
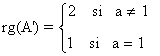
Sabido esto ya podemos discutir y resolver el sistema en función de a:
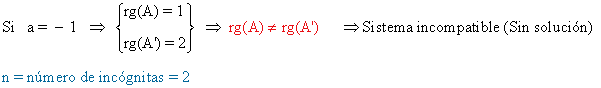

y obtenemos que
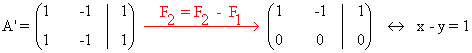
de manera que basta resolver el sistema equivalente x - y = 1. Para ello se considera y = λ
y de manera que las soluciones son:
![]()
Finalmente
Resolvemos el sistema por el método de Cramer:

7. Discute y resuelve, según los valores del parámetro, los siguientes sistemas de ecuaciones:
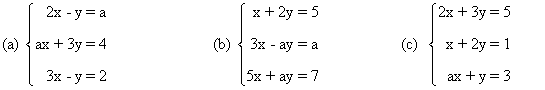
(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
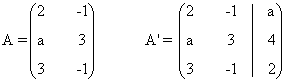
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 3 × 2. Por otra parte, el rango de A' puede ser
como mucho 3 ya que
que A' es una matriz
de orden 3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que rg(A) = 2 ya que contiene al menor no nulo de orden 2
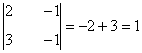
Observamos ahora que
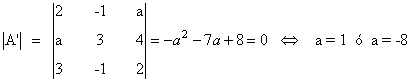
de manera que
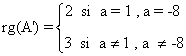
Teniendo esto en cuenta:
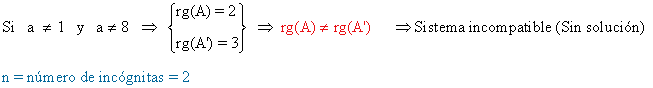
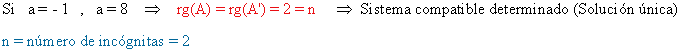
- Si a = 1 :

- Si a = 8 :

(b)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
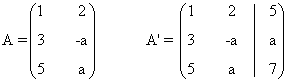
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz es una matriz de orden 3 × 2. Por otra parte, el rango de A' puede ser
como mucho 3 ya que
que A' es una matriz
de orden 3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
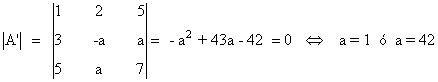
de manera que
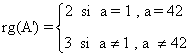
Teniendo esto en cuenta:
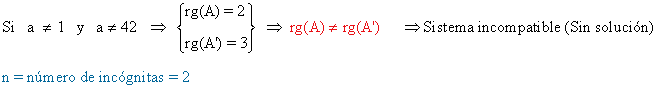
- Si a = 1, observamos que el menor de orden 2 de A
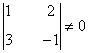
es no nulo, de manera que

Resolvemos ahora el sistema

- Si a = 42 , observamos que el menor de orden 2 de A
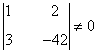
es no nulo, de manera que


(c)
8 . Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible.
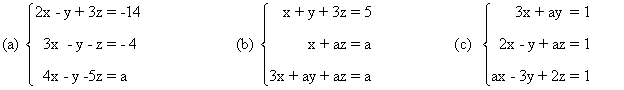
(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
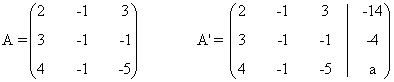
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando los rangos de A y A':
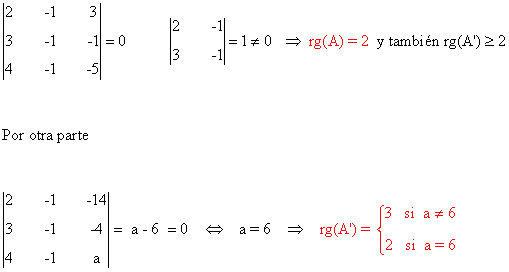
Teniendo esto en cuenta:
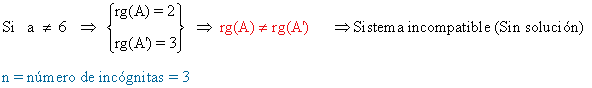

Resolvemos el sistema en este caso:
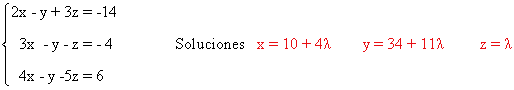
(b)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
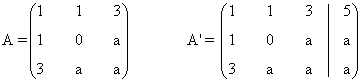
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A:
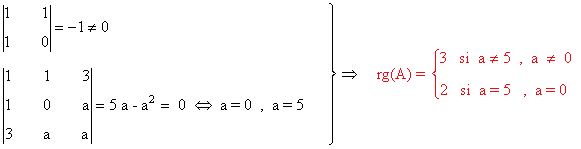
Teniendo esto en cuenta:
- Si a = 0, la matriz ampliada asociada al sistema es la siguiente:
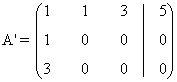
de manera que:
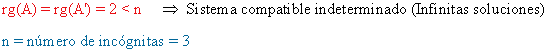
Resolviendo el sistema, obtenemos que:
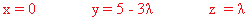
- Si a = 5, la matriz ampliada asociada al sistema es:
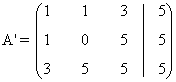
Observamos que
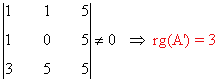
de manera que:
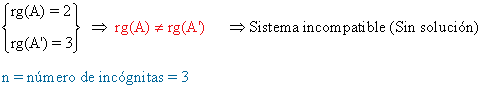
- Si a ≠ 5, a ≠ 0, entonces

Resolvemos el sistema en función de a utilizando el método de Cramer:

(c)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
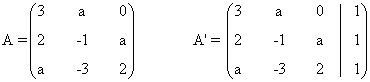
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos estudiando el rango de A:
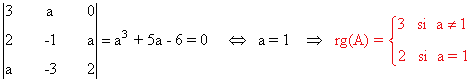
- Si a ≠1, entonces

Resolvemos el sistema en función de a utilizando el método de Cramer:
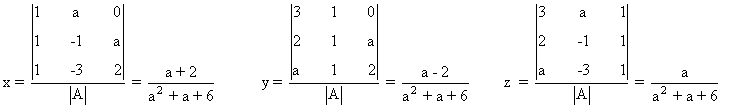
- Si a = 1, observamos que
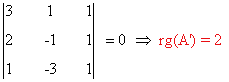
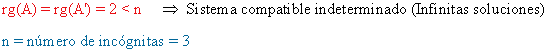
Resolvemos el sistema:
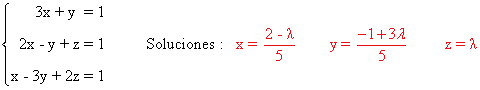
9 . Estudia los siguientes sistemas según los valores del parámetro a y resuélvelos en los casos en que sea posible.
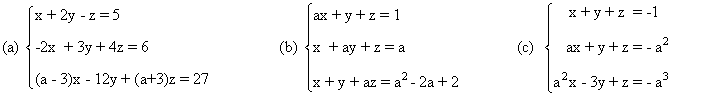
(a)
Nº de ecuaciones = Nº de incógnitas
- Para discutir el sistema se calcula primero |A|.
- Si |A'| ≠ 0 sistema compatible determinado.
- Si |A| = 0 hay que estudiar el rango de A'.
La matriz y la matriz ampliada asociadas a este sistema son las siguientes

Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Como el número de ecuaciones coincide con el de incógnitas conviene empezar estudiando el rango de A:
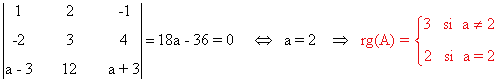
- Si a ≠ 2, entonces

Resolvemos el sistema en función de a utilizando el método de Cramer:
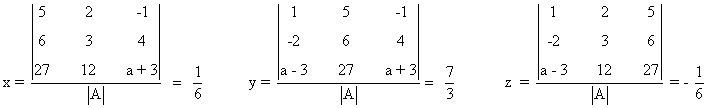
- Si a = 2, observamos que
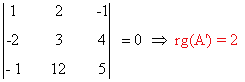
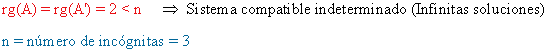
Resolvemos el sistema:
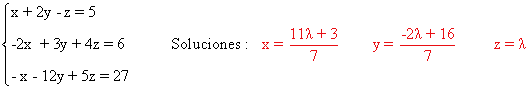
(b)
Nº de ecuaciones = Nº de incógnitas
- Para discutir el sistema se calcula primero |A|.
- Si |A'| ≠ 0 sistema compatible determinado.
- Si |A| = 0 hay que estudiar el rango de A'.
La matriz y la matriz ampliada asociadas a este sistema son las siguientes

Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos calculando |A|:
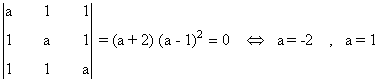
Teniendo esto en cuenta:
- Si a = 1, la matriz ampliada asociada al sistema es la siguiente:
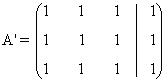
de manera que:
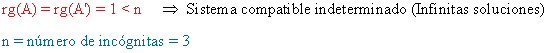
Resolviendo el sistema, obtenemos que:

- Si a = -2, la matriz ampliada asociada al sistema es:
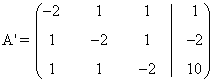
Observamos que
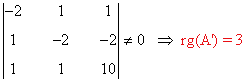
de manera que:
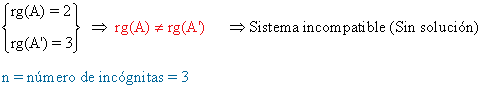
- Si a ≠1, a ≠ -2, entonces

Resolvemos el sistema en función de a utilizando el método de Cramer:
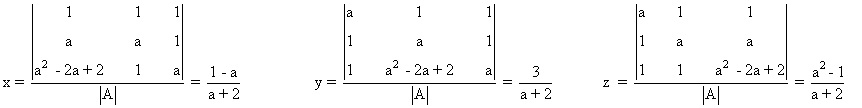
(c)
Nº de ecuaciones = Nº de incógnitas
- Para discutir el sistema se calcula primero |A|.
- Si |A'| ≠ 0 sistema compatible determinado.
- Si |A| = 0 hay que estudiar el rango de A'.
La matriz y la matriz ampliada asociadas a este sistema son las siguientes

Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz es una matriz de orden 3. También el rango de A' puede ser a lo sumo 3, ya
que A' es una matriz
de orden 3 × 4.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Como el número de ecuaciones coincide con el de incógnitas conviene empezar estudiando el rango de A:
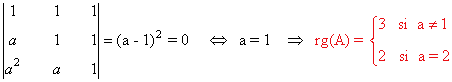
- Si a ≠ 1, entonces

Resolvemos el sistema en función de a utilizando el método de Cramer:

- Si a = 1, la matriz ampliada asociada al sistema es la siguiente:
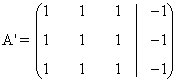
de manera que:
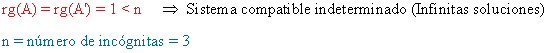
Resolviendo el sistema, obtenemos que:

10 . Estudia los siguientes sistemas homogéneos según los valores del parámetro a y resuélvelos en los casos en que sea posible.

(a)
rg(A) = n ⇒ Solución única (solución trivial)
rg(A) < n ⇒ Infinitas soluciones ( soluciones no triviales)
En este caso n = número de incógnitas = 3. Empezamos expresando matricialmente el sistema:
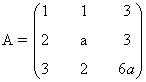
Observamos que
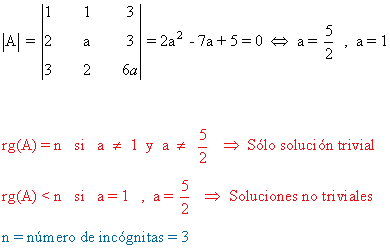
La primera y la última fila aportan un menor de orden 2 no nulo:
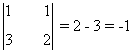
Esto nos dice que dichas filas son linealmente independientes. Como el rango de la matriz es 2, la
segunda fila puede entonces obtenerse como combinación lineal de estas, de manera que podemos
obviarla a la hora de calcular la solución del sistema. Así:
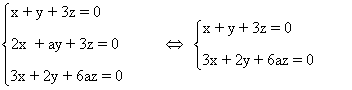
- Si a = 1,
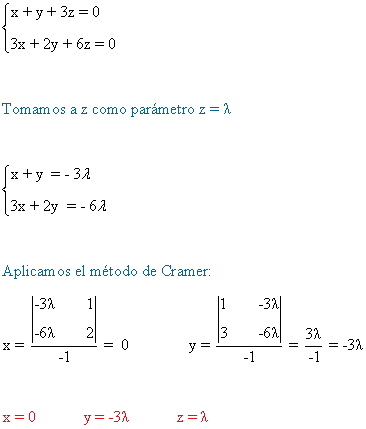
- Si a = 5/2,
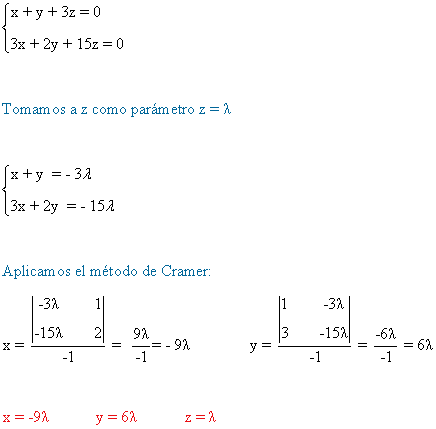
(b)
rg(A) = n ⇒ Solución única (solución trivial)
rg(A) < n ⇒ Infinitas soluciones ( soluciones no triviales)
En este caso n = número de incógnitas = 3. Empezamos expresando matricialmente el sistema:
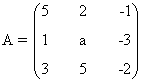
Observamos que

Si a = 8, observamos que la primera y la última fila aportan un menor de orden 2 no nulo:
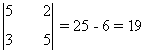
Esto nos dice que dichas filas son linealmente independientes. Como el rango de la matriz es 2, la
segunda fila puede entonces obtenerse como combinación lineal de estas, de manera que podemos
obviarla a la hora de calcular la solución del sistema. Así:
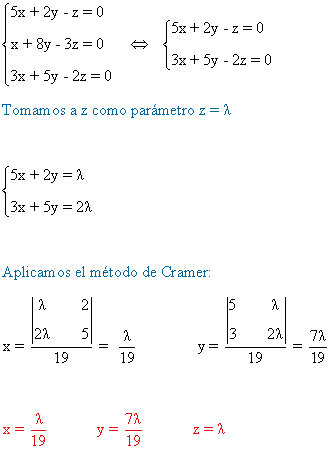
11 . Estudia los siguientes sistemas homogéneos según los valores del parámetro a y resuélvelos en los casos en que sea posible.

(a)
rg(A) = n ⇒ Solución única (solución trivial)
rg(A) < n ⇒ Infinitas soluciones ( soluciones no triviales)
En este caso n = número de incógnitas = 3. Empezamos expresando matricialmente el sistema:
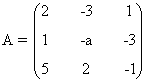
Observamos que

Si a = - 8, observamos que la primera y la última fila aportan un menor de orden 2 no nulo:
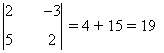
Esto nos dice que dichas filas son linealmente independientes. Como el rango de la matriz es 2, la
segunda fila puede entonces obtenerse como combinación lineal de estas, de manera que podemos
obviarla a la hora de calcular la solución del sistema. Así:
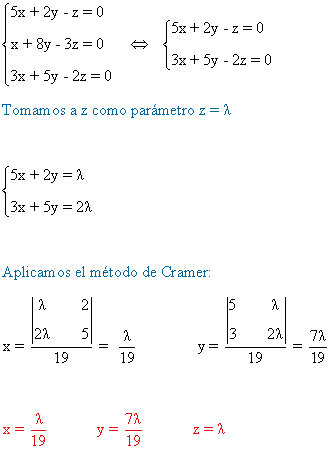
(b)
rg(A) = n ⇒ Solución única (solución trivial)
rg(A) < n ⇒ Infinitas soluciones ( soluciones no triviales)
En este caso n = número de incógnitas = 3. Empezamos expresando matricialmente el sistema:
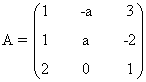
Observamos que

Observamos que la primera y la segunda fila aportan un menor de orden 2 no nulo. Esto nos dice que
dichas filas son linealmente independientes. Como el rango de la matriz es 2, la tercera fila puede
entonces obtenerse como combinación lineal de estas, de manera que podemos
obviarla a la hora de
calcular la solución del sistema. Así:

12 . Discute y resuelve, según los valores del parámetro, los siguientes sistemas:

(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
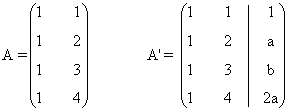
Para este sistema n = número de incognitas = 2. Observamos que el rango de A puede ser a lo sumo
2 ya que A es una
matriz 4 ×2. El rango de A' puede ser a lo sumo 3, ya que A' es una matriz
de
orden 4 × 3.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
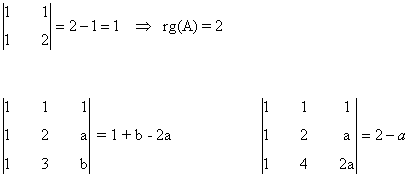
Si 1 + b - 2a ≠ 0 ó 2 - a ≠ 0 entonces el sistema es incompatible ya que rg(A) ≠ rg(A')
Si 1 + b - 2a = 0 y 2 - a = 0 entonces
rg(A') =rg(A)= n n = número de incognitas = 2
y el sistema es compatible determinado y además a = 2 y b = 3.
Como las dos primeras filas aportan un menor no nulo, sabemos que son linealmente independientes. Unido esto al
hecho de que la matriz A tiene rango 2, obtenemos que basta resolver el sistema dado por las dos primeras filas:
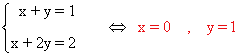
(b)
rg(A) = n ⇒ Solución única (solución trivial)
rg(A) < n ⇒ Infinitas soluciones ( soluciones no triviales)
Este sistema es homogéneo con tres ecuaciones y tres incógnitas y su matriz asociada es:
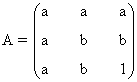
Empezamos calculando |A| :
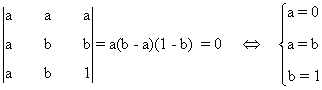
- Si |A|≠ 0 el sistema es compatible determinado y su única solución es la trivial.
- Si a = 0 la matriz asociada al sistema es
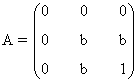
- Si b = 0
la matriz asociada al sistema es
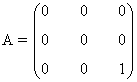
de manera que el sistema que se obtiene es
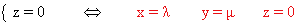
- Si b = 1 la matriz asociada al sistema es
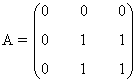
de manera que el sistema que se obtiene es
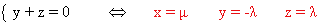
- Si b ≠ 0 y b ≠ 1 el sistema que se obtiene es:
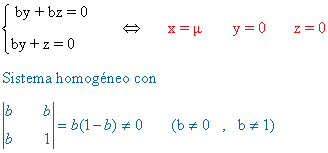
- Si b = 0
la matriz asociada al sistema es
- Si 0 ≠ a = b
- Si a = b = 1 el sistema que se obtiene es:
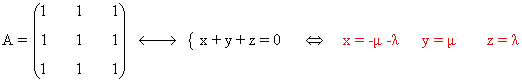
- Si a = b y b ≠ 1 el sistema que se obtiene es:
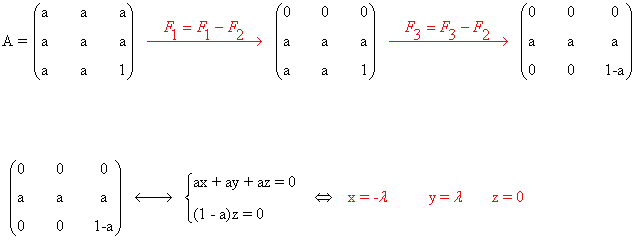
- Si a = b = 1 el sistema que se obtiene es:
- Si a≠0, a ≠ b, b = 1 la matriz asociada al sistema y la solución del mismo son los que siguen:
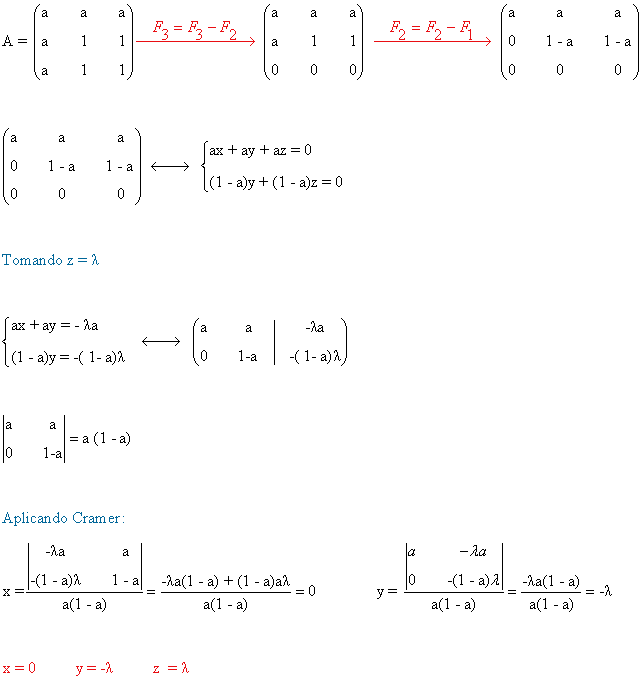
13 . Discute y resuelve, según los valores del parámetro, los siguientes sistemas:

(a)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
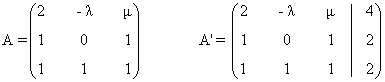
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz de orden 3. El rango de A' puede ser a lo sumo 3, ya que A' es una matriz
de
orden 3 × 4.
Empezamos calculando |A| :
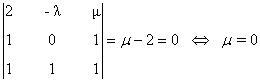
- Si μ ≠ 2 entonces
rg(A) = rg(A') = n (n = número de incognitas = 3)
de manera que el sistema es compatible determinado. Lo resolvemos:
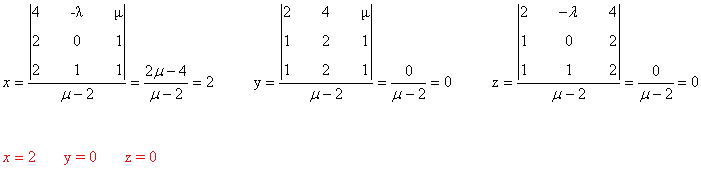
- Si μ = 2 entonces

rg(A) = rg(A') = 2 < n (n = número de incognitas = 3)
de manera que el sistema es compatible indeterminado. Lo resolvemos. Como las dos últimas filas aportan un
menor de orden 2 no nulo, dichas filas son linealmente independientes, de manera que la primera fila puede
obtenerse como combinación lineal de estas, ya que rg(A)=rg(A')=2. Podemos pues resolver el sistema que
generan dichas filas y su solución será la del sistema completo:
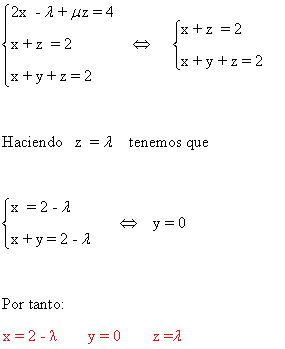
(b)
La matriz y la matriz ampliada asociadas a este sistema son las siguientes
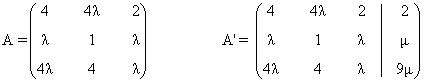
Para este sistema n = número de incognitas = 3. Observamos que el rango de A puede ser a lo sumo
3 ya que A es una
matriz de orden 3. El rango de A' puede ser a lo sumo 3, ya que A' es una matriz
de
orden 3 × 4.
Empezamos viendo cuándo se anula |A|:
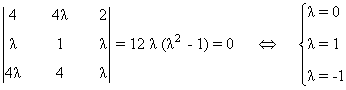
- Si λ ≠ 0 , λ ≠ -1, λ ≠ 1 entonces |A| ≠ 0 de manera que
rg(A) = rg(A') = n (n = número de incognitas = 3)
y el sistema es compatible determinado y aplicando Cramer:
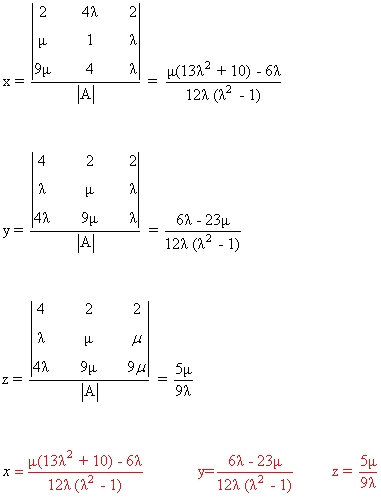
- Si λ = 0 se tiene que
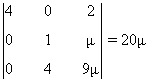
de manera que- Si μ ≠ 0 entonces
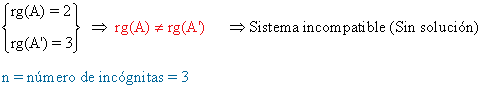
- Si μ = 0 entonces
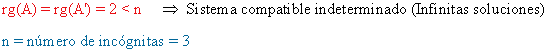
Resolvemos el sistema:
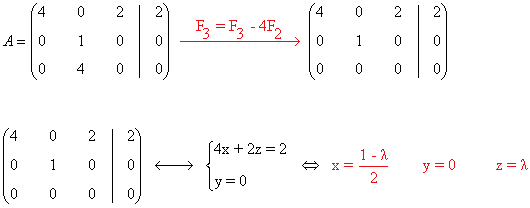
- Si μ ≠ 0 entonces
- Si λ = 1 se tiene que
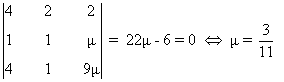
de manera que- Si μ ≠ 3/11 entonces
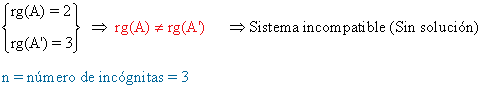
- Si μ = 3/11 entonces
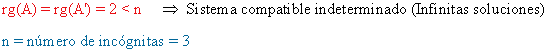
Resolvemos el sistema:
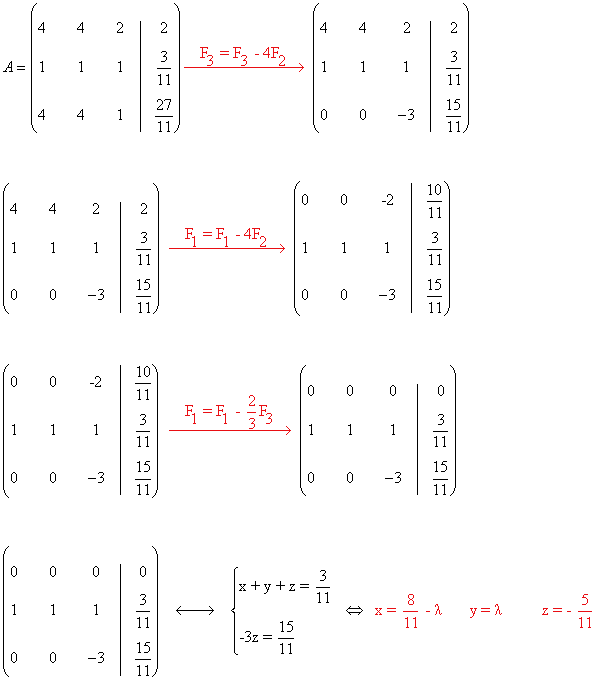
- Si μ ≠ 3/11 entonces
- Si λ = -1 se tiene que
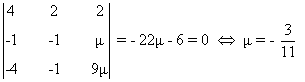
de manera que- Si μ ≠ - 3/11 entonces
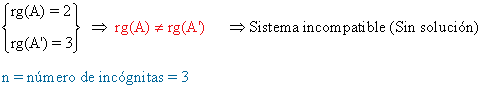
- Si μ = - 3/11 entonces
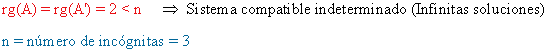
Resolvemos el sistema:
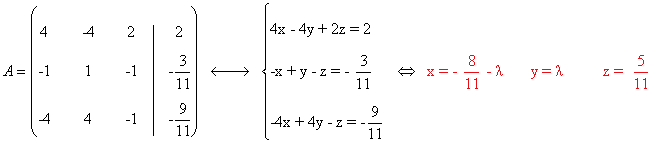
- Si μ ≠ - 3/11 entonces
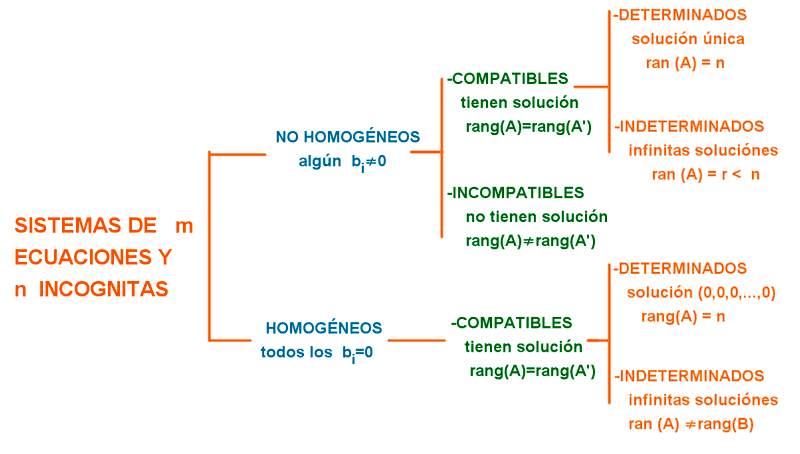
Nº de ecuaciones < Nº de incógnitas
- No puede ser compatible determinado.
- Puede ser incompatible (basta que haya dos ecuaciones contradictorias).
Nº de ecuaciones = Nº de incógnitas + 1
- Es un sistema que tiene una ecuación más que incógnitas.
- Para discutir el sistema se calcula primero |A'|.
- Si |A'| ≠ 0 sistema incompatible.
Nº de ecuaciones = Nº de incógnitas
- Para discutir el sistema se calcula primero |A|.
- Si |A'| ≠ 0 sistema compatible determinado.
- Si |A| = 0 hay que estudiar el rango de A'.


 INICIO
INICIO