Ejercicios resueltos de sistemas de ecuaciones mediante la regla de Cramer
1) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
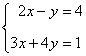
2) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
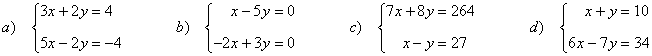
3) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
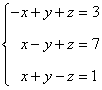
4) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
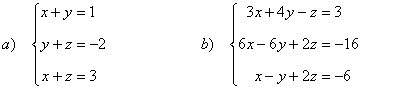
5) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:

6) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
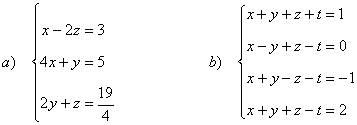
7) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
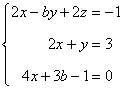
8) Fórmula de la regla de Cramer
1) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
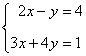
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
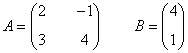
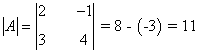
Observamos que |A| = 11 ≠ 0 de manera que podemos aplicar la regla de Cramer:
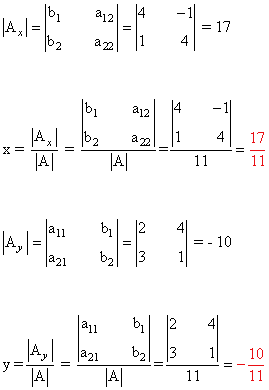
2) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
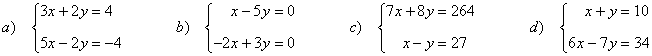
(a)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
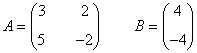
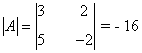
Observamos que |A| = - 16 ≠ 0 de manera que podemos aplicar la regla de Cramer:
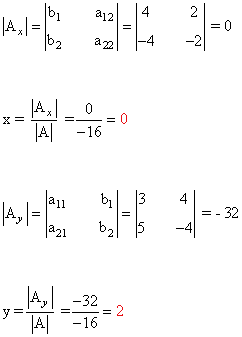
(b)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
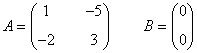
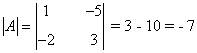
Observamos que |A| = - 7 ≠ 0 de manera que podemos aplicar la regla de Cramer:
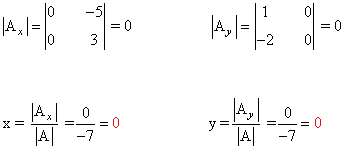
(c)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
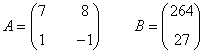
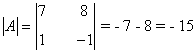
Observamos que |A| = - 15 ≠ 0 de manera que podemos aplicar la regla de Cramer:
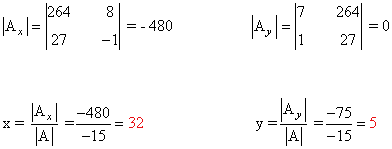
(d)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
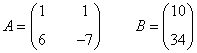
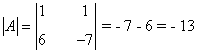
Observamos que |A| = - 13 ≠ 0 de manera que podemos aplicar la regla de Cramer:
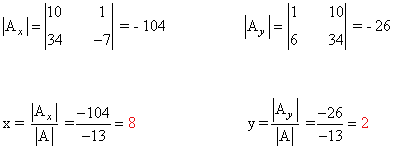
3) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
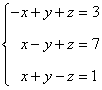
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
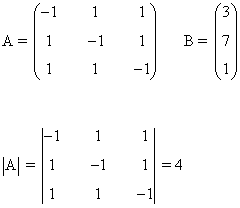
Observamos que |A| = 4 ≠ 0 de manera que podemos aplicar la regla de Cramer:
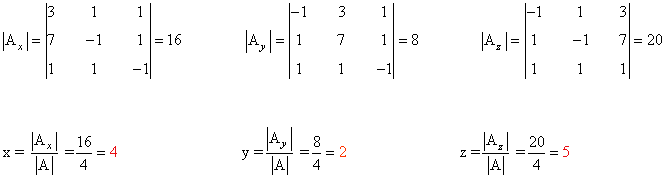
4) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
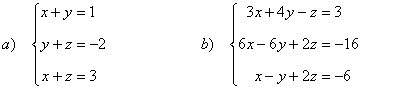
(a)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
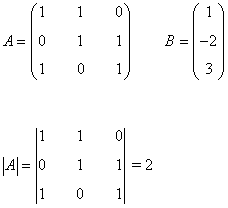
Observamos que |A| = 2 ≠ 0 de manera que podemos aplicar la regla de Cramer:
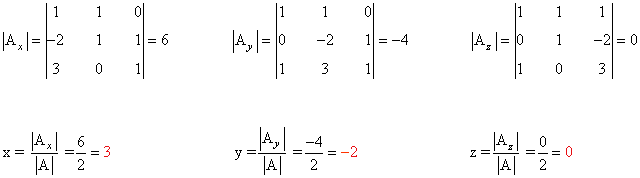
(b)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
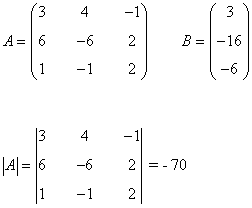
Observamos que |A| = - 70 ≠ 0 de manera que podemos aplicar la regla de Cramer:
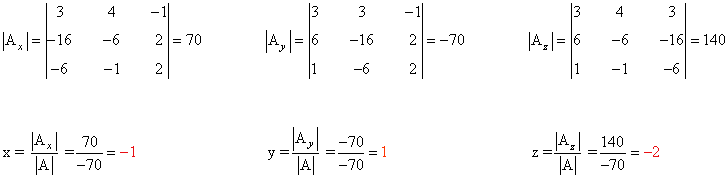
5) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:

(a)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
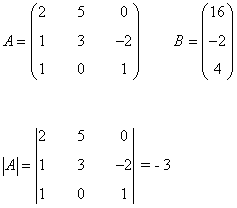
Observamos que |A| = - 3 ≠ 0 de manera que podemos aplicar la regla de Cramer:
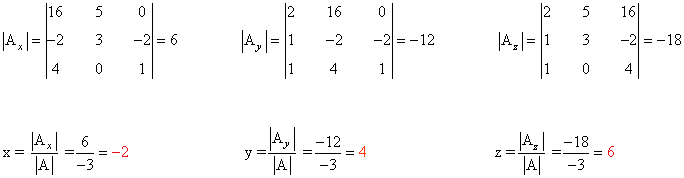
(b)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
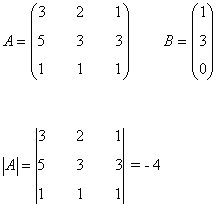
Observamos que |A| = - 4 ≠ 0 de manera que podemos aplicar la regla de Cramer:
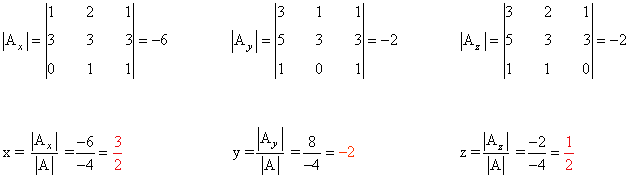
6) Resolver los siguientes sistemas de ecuaciones mediante la regla de Cramer:
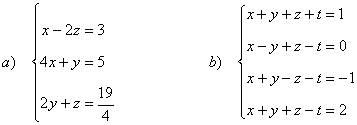
(a)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
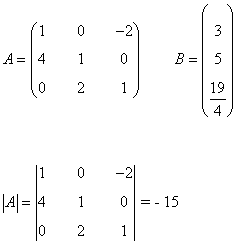
Observamos que |A| = -15 ≠ 0 de manera que podemos aplicar la regla de Cramer:
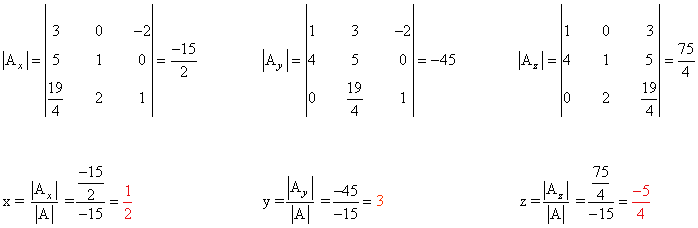
(b)
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
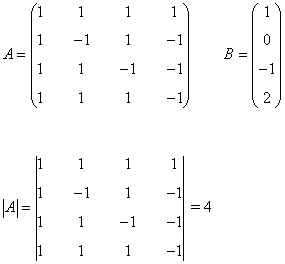
Observamos que |A| = 4 ≠ 0 de manera que podemos aplicar la regla de Cramer:
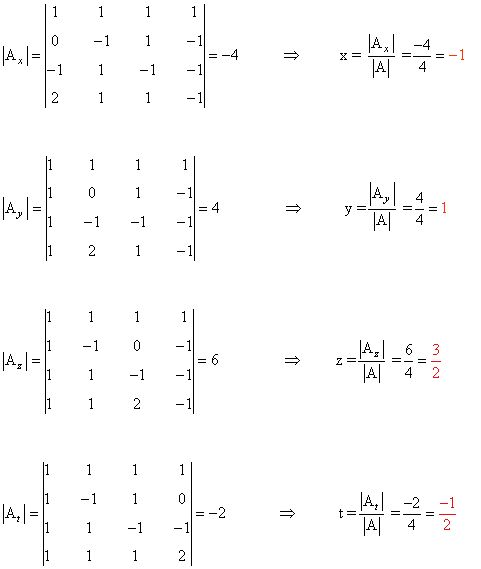
7) Resolver el siguiente sistema de ecuaciones mediante la regla de Cramer:
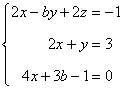
En primer lugar reescribimos el sistema de ecuaciones para definir las matrices A y B:
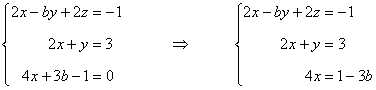
La matriz de coeficientes A y la matriz de términos independientes B son las siguientes:
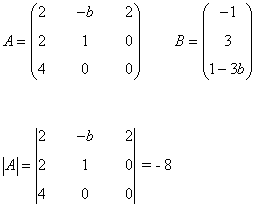
Observamos que |A| = - 8 ≠ 0 de manera que podemos aplicar la regla de Cramer para cualquier valor de b :
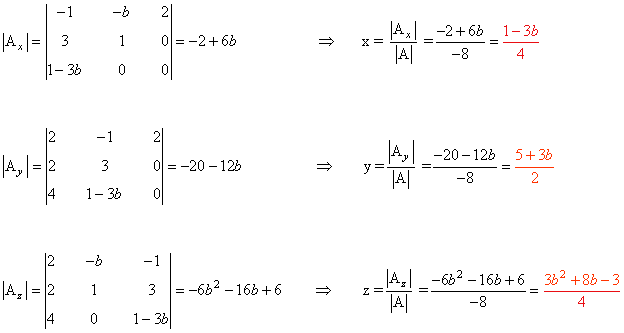
Dado un sistema de n ecuaciones y n incógnitas:
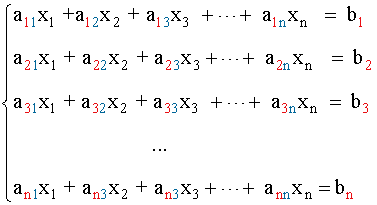
que podemos expresar matricialmente como
A · X = B.
Si |A| ≠ 0, entonces el sistema A · X = B posee solución única que viene dada de la siguiente forma:
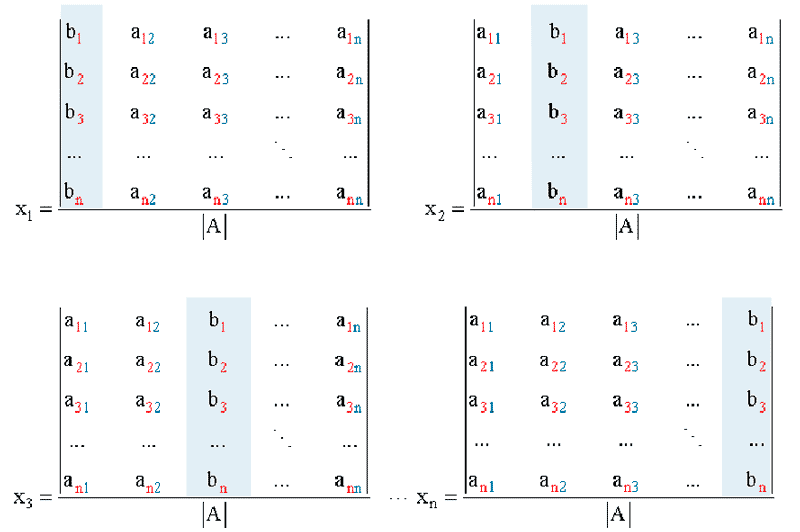


 INICIO
INICIO