Cálculo del rango de una matriz por el método de Gauss
Matriz escalonada
Una matriz es una matriz escalonada si:
- En el caso de tener cierto número de filas nulas estas se sitúan en la parte inferior de la matriz.
- En las filas no nulas, el primer elemento diferenente de cero de cada fila está situado más a la derecha que el primer elemento no nulo de la fila inmediatamente superior.
Ejemplos de matrices escalonadas
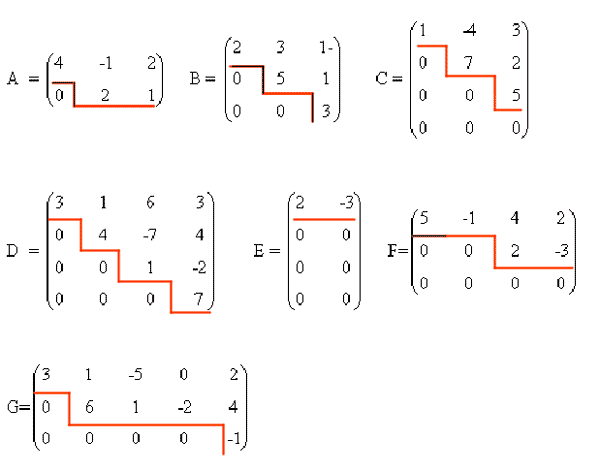
Ejemplos de matrices no escalonadas
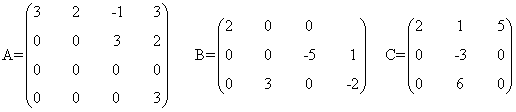
El rango de una matriz escalonada A es el número de filas no nulas de la matriz. Se denomina por rg(A).
Siempre es posible pasar de una matriz cualquiera A a una matriz escalonada. Para esto se llevan a cabo transformaciones elementales, que son las siguientes:
- Cambiar el orden de las filas.
- Multiplicar una o más filas por un número real distinto de cero.
- Sumar a una fila otra multiplicada por un número real.
Las matrices que se obtienen mediante estas transformaciones elementales son equivalentes.
El rango de una matriz A es el rango de una matriz escalonada equivalente a A.
Ejemplos de cálculo de rango de matrices
1) Calcular el rango de la siguiente matriz por el método de Gauss:
Método de Gauss
- Cambiar el orden de las filas: Fi ↔ Fj
- Multiplicar una o más filas por un número real distinto de cero: Fi → k Fj
- Sumar a una fila otra multiplicada por un número real: Fi → Fi + k Fj
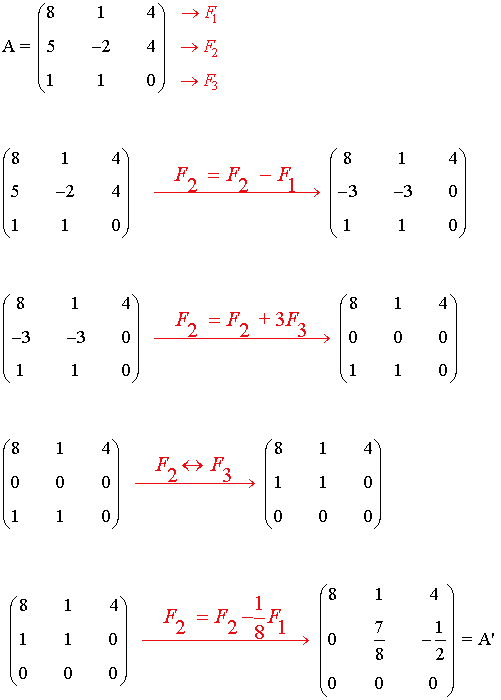
La matriz A' es una matriz escalonada equivalente a A y tiene 2 filas no nulas. Por tanto rg(A)=2.
2) Calcular el rango de la siguiente matriz por el método de Gauss:
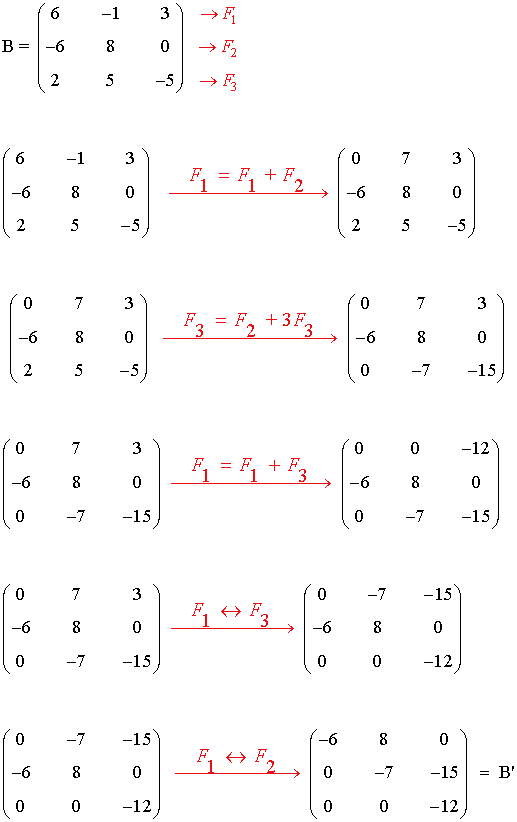
La matriz B' es una matriz escalonada equivalente a B y tiene 3 filas no nulas. Por tanto rg(B)=3.


 INICIO
INICIO

