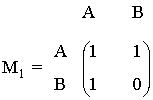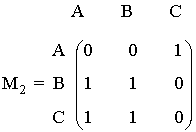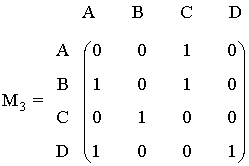Matrices y grafos
Grafos
Un grafo está definido por un conjunto de puntos, llamados vértices o nodos y un conjunto de pares de vértices, denominados aristas o arcos.
Podemos considerar un grafo con vértices { a, b, c, d, e } y aristas { ab, ad, ae, bc, cd, de }
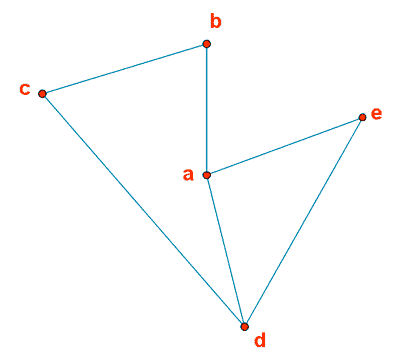
Como podemos ver en el ejemplo, los vértices se representan como puntos y cada arista entre dos vértices como una línea que une dichos vértices.
Un grafo no dirigido es aquel que tiene sus aristas o arcos sin orientar.
Un grafo dirigido o digrafo es aquel que tiene sus aristas o arcos orientados, es decir, sus aristas vienen dadas por pares ordenados.
Podemos considerar un grafo dirigido con vértices { a, b, c, d, e } y aristas { ab, ae, bc, bd, cd, da }
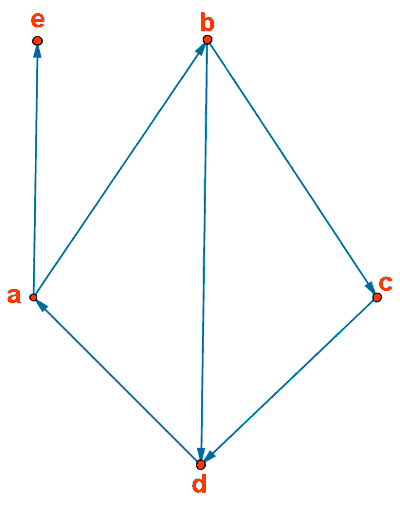
En este caso también los vértices se representan como puntos. Las aristas se representan como flechas que parten de un vértice (el primero de cada par) y llegan a otro (el segundo de cada par).
Matriz de adyacencia o asociada
Ejemplos de matrices de adyacencia
1) Construcción de la matriz de adyacencia de un grafo no dirigido:
Para construir las matrices de adyacencia, ordenamos los vértices, por ejemplo
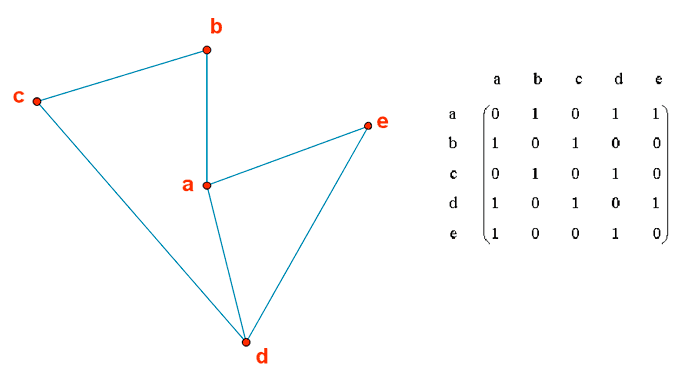
Si tenemos una arista que une los vértices a y b, en la matriz de adyacencia tenemos que poner un 1 tanto en la posición ab como en la posición ba.
La matriz de adyacencia de los grafos no dirigidos siempre es simétrica.
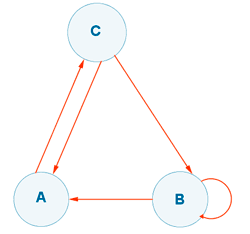
2) Construcción de la matriz de adyacencia de un grafo dirigido:
Para construir las matrices de adyacencia, ordenamos los vértices, por ejemplo:

Si tenemos una flecha que parte del vértice a y llega al vértice e , ponemos un 1 en la posición ae de la matriz de adyacencia. En caso de no tener esa flecha ponemos un 0.
La matriz de adyacencia de un grafo no dirigido no tiene por qué ser simétrica.
3) Escribe las matrices de adyacencia o asociadas a cada uno de los siguientes grafos:
Camino y longitud de un camino
Llamaremos camino entre los vértices a y b a cualquier sucesión de aristas que conecte a y b. La longitud del camino será el número de aristas que lo componen.
Ejemplos de caminos y longitud de caminos
El mapa de las caminos de una isla entre las casas de los vecinos viene dado por el siguiente grafo (las aristas representan caminos y los vértices casas):

Hallar cuántos caminos de longitud 2 y 3 conectan cada par de casas de dicho mapa.
Empezamos construyendo la matriz de adyacencia:


Todos los caminos de longitud 2 entre dos vértices vendrán dados por la matriz C2 y los de longitud 3 por la matriz C3.
¿Cuántos y cuáles son los caminos de longitud 2 que unen las casas b y d?
A la vista de la matriz C2 sabemos que hay exactamente 2 rutas de longitud 2 que son:
d → c → b
d → a → b
¿Cuántos y cuáles son los caminos de longitud 3 que unen las casas a y d?
A la vista de la matriz C3 sabemos que hay exactamente 6 caminos de longitud 3 que unen las casas a y d que son los siguientes:
a → b → c → d a → b → a → d
a → e → a → d a → d → e → d
a → d → a → d a → d → c → d
Aplicación de grafos a la psicología
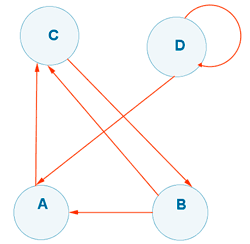
El psicólogo de una empresa está estudiando la relación de dominio o ascendiente de un grupo de trabajo de 5 personas: Aurelia, Berta, Carlos, Daniela, Esteban. Mediante entrevistas personales, consigue establecer quién domina a quien por parejas. Empleando los datos que obtiene, elabora el siguiente grafo dirigido de 5 vértices donde, por ejemplo, A → B significa que Aurelia domina a Berta.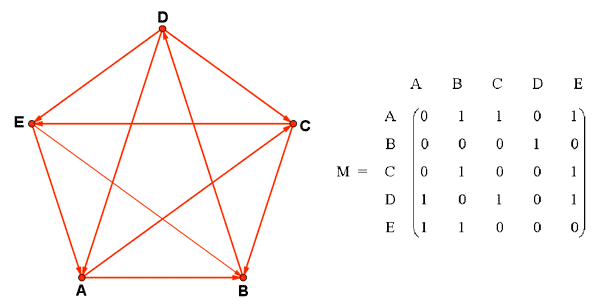
Para ver quien es el lider del grupo se suman las filas de la matriz de adyacencia. Con esto se obtiene a cuantos compañeros domina cada persona. En este caso obtenemos que
- Aurelia domina a 3 personas.
- Berta domina a 1 persona.
- Carlos domina a 2 personas.
- Daniela domina a 3 personas.
- Esteban domina a 2 personas.
Tanto Aurelia como Daniela dominan a 3 personas. Este empate hace que no sea posible decidir quién es el lider del grupo.
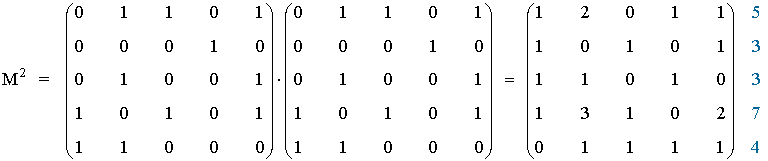
La matriz M2, tal como hemos visto en el ejemplo anterior, representa a caminos de longitud 2. En términos del problema que estamos tratando, esto representa los dominios "de segundo orden", es decir, la cantidad de personas que son dominadas por personas que domina cierta persona. Por ejemplo, si Daniela domina a Carlos y Carlos domina a Berta, tiene sentido pensar que Daniela puede ejercer algún tipo de dominio sobre Berta. Sumando como antes, obtenemos cuantos dominios de segundo orden ejerce cada persona.
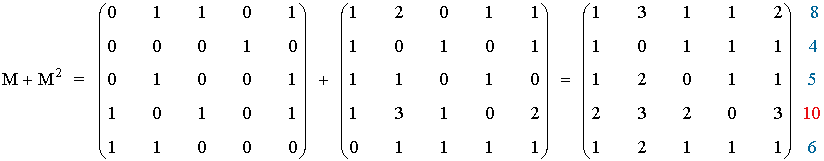
Finalmente, la matriz M + M2 representa la cantidad de dominios de primer o segundo orden que ejerce cada persona sobre el resto de personas del grupo. Sumando el número de filas de esta matriz, podemos declarar a Daniela como líder del grupo.


 INICIO
INICIO