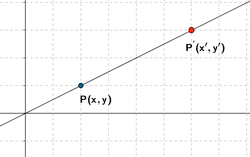
Aplicación de las matrices: Movimientos en el plano
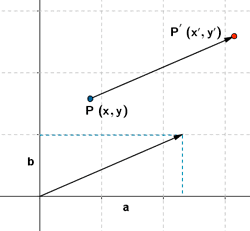
Sea P(x,y) un punto cualquiera del plano. Sea P(x',y') su transformado.
Traslación con vector guía (a,b)
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
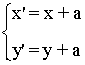 |
 |
Simetría respecto del eje X
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
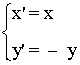 |
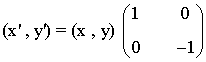 |
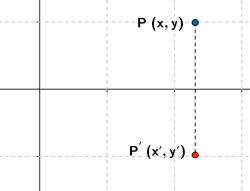 |
Simetría respecto del eje Y
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
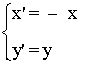 |
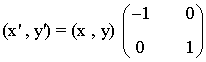 |
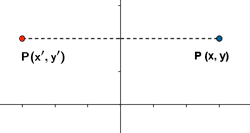 |
Simetría respecto del origen
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
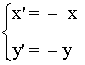 |
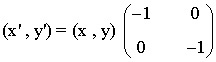 |
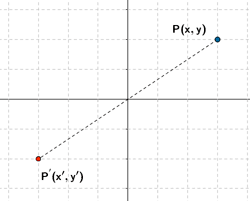 |
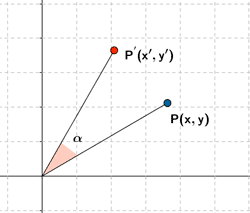
Giro de centro O y ángulo α
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
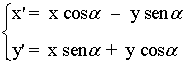 |
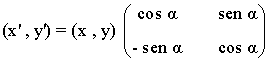 |
 |
Homotecia de centro O y razón k ≠ O
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
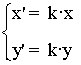 |
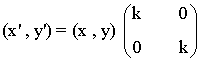 |
 |
Las matrices asociadas a los movimientos (salvo la traslación) son las siguientes:
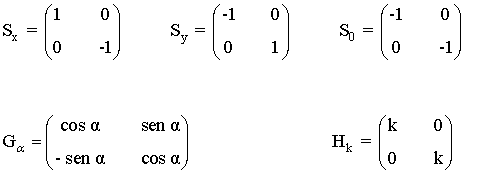
y son todas inversibles.
Observamos además que si consideramos dos movimientos cualesquiera entre los anteriores, la composición de dichos movimientos tiene como matriz asociada al producto de las matrices asociadas a los movimientos. En otras palabras, si consideramos dos movimientos m1 y m2 con matrices asociadas M1 y M2, la composición de los mismos, que es m1 o m2, tiene como matriz asociada a la matriz M1 · M2 .
Ejemplo de movimientos en el plano
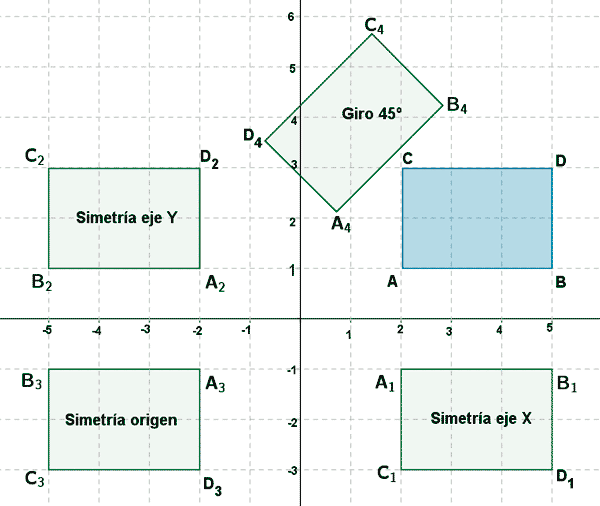
El rectángulo de la figura tiene por vértices A = ( 2, 1 ) B = (5 , 1) C = ( 5, 3 ) D = ( 2, 3 ). Estas coordenadas pueden escribirse matricialmente como:
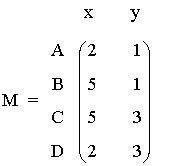
¿Cómo se modifica el rectángulo inicial al aplicarle las transformaciones asociadas a las siguientes matrices?
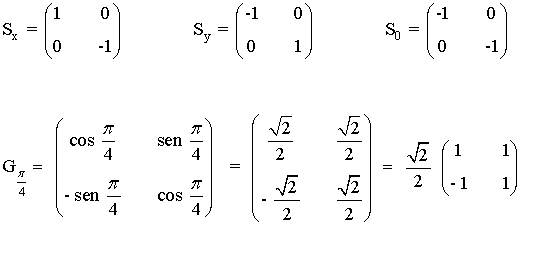
Se modifica como vemos a continuación:
Para la simetría respecto al eje X, que tiene matriz asociada Sx
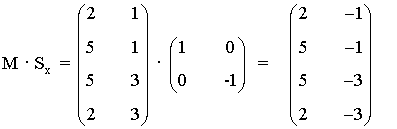
de manera que el rectángulo obtenido al aplicar Sx al rectángulo inicial tiene vértices
A1 = ( 2 , -1 ) , B1 = ( 5 , -1 ) , C1 = ( 5 , -3 ) , D1 = ( 2 , -3 ).
Para la simetría respecto al eje Y, que tiene matriz asociada Sy
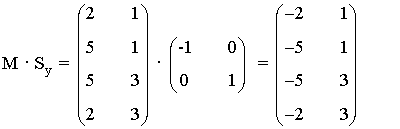
de manera que el rectángulo obtenido al aplicar Sy al rectángulo inicial tiene vértices
A2 = ( -2 , 1 ) , B2 = ( -5 , 1 ) , C2 = ( -5 , 3 ) , D2 = ( -2 , 3 ).
Para la simetría respecto al origen, que tiene matriz asociada S0
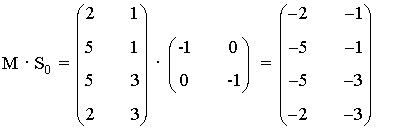
de manera que el rectángulo obtenido al aplicar S0 al rectángulo inicial tiene vértices
A3 = ( -2 , -1 ) , B3 = ( -5 , -1 ) , C3 = ( -5 , -3 ) , D3 = ( -2 , -3 ).
Para la simetría respecto al origen, que tiene matriz asociada S0
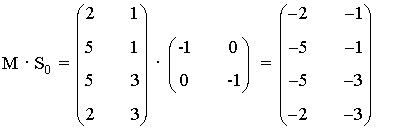
de manera que el rectángulo obtenido al aplicar S0 al rectángulo inicial tiene vértices
A3 = ( -2 , -1 ) , B3 = ( -5 , -1 ) , C3 = ( -5 , -3 ) , D3 = ( -2 , -3 ).
Para el giro de 45 grados que tiene, que tiene matriz asociada Sπ/4
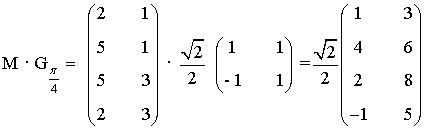
de manera que el rectángulo obtenido al aplicar Sπ/4 al rectángulo inicial tiene vértices
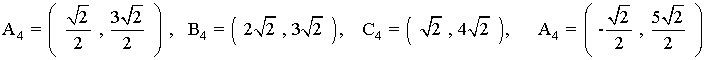


 INICIO
INICIO
