Ejercicios resueltos de intervalos y entornos.
Operaciones con unión e intersección de intervalos.
- Resumen
- 1. Expresa como intervalo I
- 2. II
- 3. Unión e intersección
- 4. Entornos
- 5. Intervalos a entornos
Desigualdades e intervalos
| Nombre | Intervalo | Desigualdad | Conjunto solución | Gráfica |
|---|---|---|---|---|
| Intervalo abierto | (a , b) | a < x < b | { x | a < x < b} | |
| Intervalo cerrado | [a , b] | a ≤ x ≤ b | { x | a ≤ x ≤ b} | |
| Intervalo semiabierto | (a , b] | a < x ≤ b | { x | a < x ≤ b} | |
| Intervalo semiabierto | [a , b) | a ≤ x < b | { x | a ≤ x < b} | |
| Intervalo no acotado | (a , ∞) | a < x | { x | a < x } | |
| [a , ∞) | a ≤ x | { x | a ≤ x } | ||
| (-∞ , b) | x < b | { x | x < b } | ||
| (-∞ , b] | x ≤ b | { x | x ≤ b } | ||
| (-∞ , + ∞) | -∞ < x < + ∞ | { x | x ∈ R } |
1) Expresa los siguientes conjuntos en forma de intervalo, y represéntalos gráficamente:
![]()

![]()

![]()



![]()

![]()

![]()

![]()

![]()


![]()
2) Expresa los siguientes conjuntos en forma de intervalo, y represéntalos gráficamente:
![]()

![]()
No hay ningún número real que en valor absoluto sea menor que -3
![]()
![]()

![]()

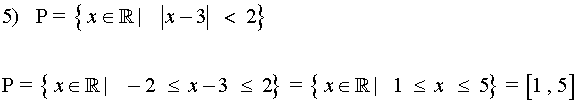

3) Opera con los siguientes conjuntos: unión e intersección



4) Define los siguientes entornos, y represéntalos gráficamente:

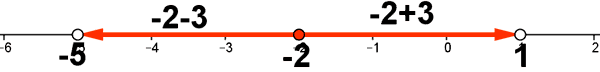
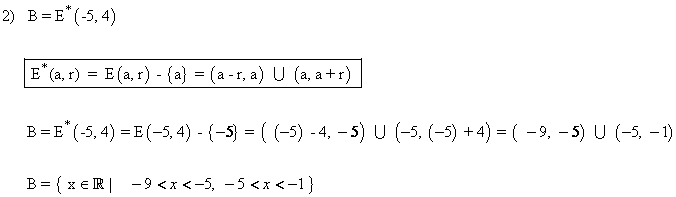

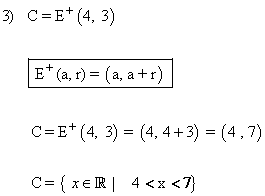
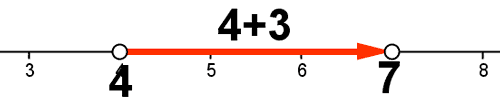
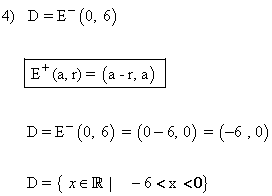
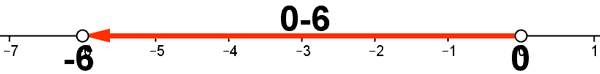
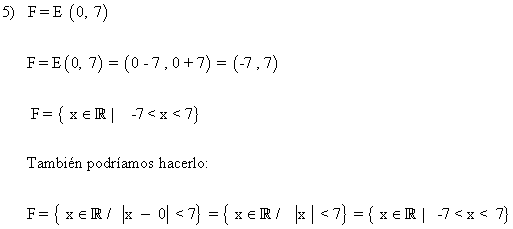
![]()
5) Expresa como entornos los siguientes intervalos:




 INICIO
INICIO