Ejercicios resueltos de triángulos rectángulos II:
Problemas prácticos y puntos inaccesibles
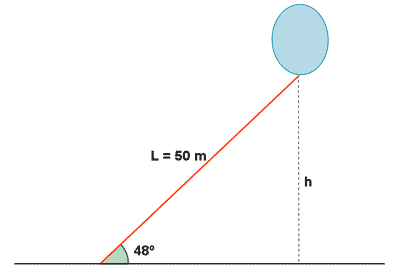
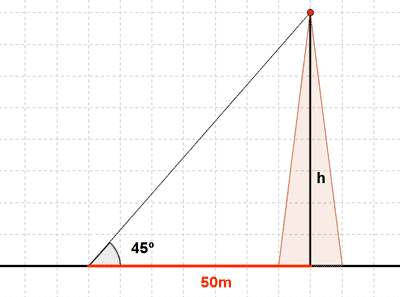
1) Un globo está sujeto al suelo mediante un cordel de 50 m de largo, que forma con el suelo un ángulo de 48º por efecto del viento. Suponiendo que nuestro cordel está completamente recto, calcular la altura del globo.
2) Se recorren 150 m en una carretera salvando un desnivel de 10 m. ¿Cual es el ángulo de inclinación de la carretera?
3) Desde un punto en el suelo situado a 50 m del pie de una antena, se traza la visual a la cúspide de la antena con un ángulo de 48º. ¿ cuál es la altura de la antena?
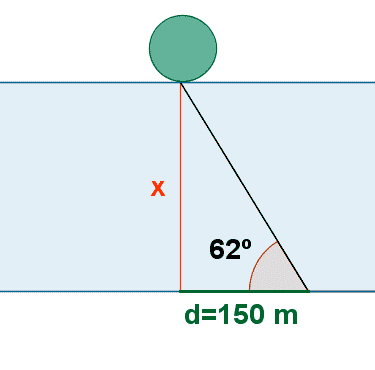
4) Juan y Pedro ven un árbol en la otra orilla del río que está frente a ellos. Al caminar Juan por la orilla una distancia de 150 metros observa que el ángulo formado entre la orilla y el árbol es de 62º. ¿Cuál es el ancho del río?
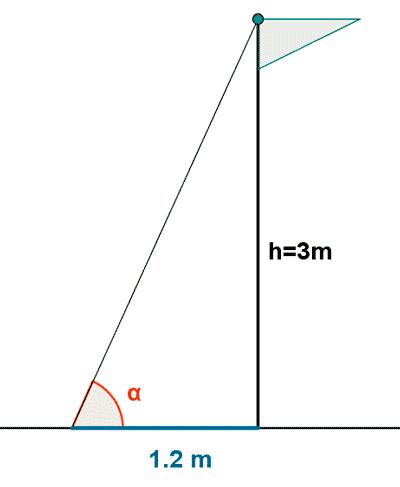
5) ¿Cuál es la inclinación de los rayos del sol si un mástil de una bandera de 3m de altura proyecta una sombra sobre el suelo de 1.2 m?
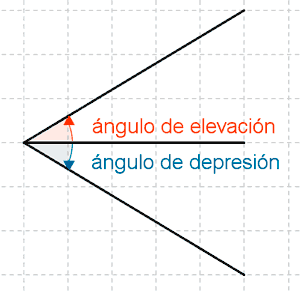
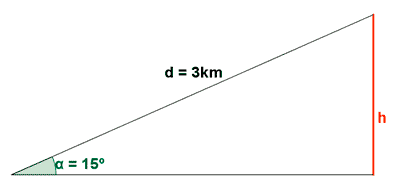
6) Un avión despega desde Barajas y lleva recorrido una distancia de 3 Km. Si el ángulo de elevación es de 15º. Calcular la altura del avión.
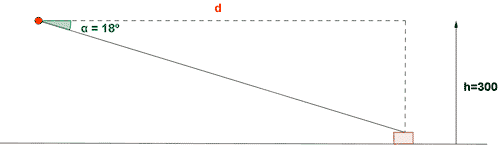
7) Un piloto que vuela a una altitud de 300 m señala que su ángulo de depresión a la torre de control es de 18 °. Si el avión sigue volando a esta altitud hacia la torre de control, ¿ cuantos metros tiene que recorrer para llegar a la torre ?
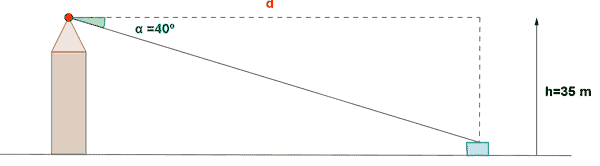
8) Desde un faro colocado a 35 m sobre el nivel del mar el ángulo de depresión de un barco es de 40º. ¿A que distancia del faro se halla el barco?
9) Si los dos brazos de un compás forman un ángulo de 60º y su longitud es de 10 cm. Hallar la distancia entre las puntas de los brazos.
10) Se quiere medir la anchura de un río. Para ello se observa un árbol que está en la otra orilla a la parte más alta y se obtine un ángulo de elevación de 55º. Alejándose 5m del río en la misma dirección del árbol se vuelve a medir el ángulo de elecvación y se obtiene 42º. Calcula la anchura del río y la altura del árbol.
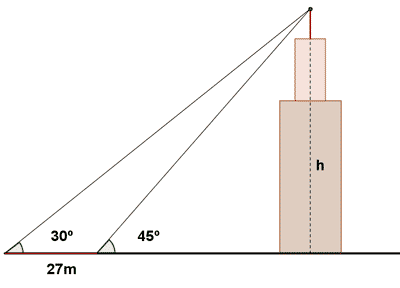
11) Dos amigos están en la base de una torre. Uno de ellos ve el extremo de la antena de la torre con un ángulo de 30º respecto a la horizontal y el otro con un ángulo de 45º. Si la distancia entre ambos es de 27 m, calcular la altura de la torre con su antena.
12) Dos focos situados en el suelo y en lados distintos, iluminan el campanario de una iglesia. La suma de las distancias de los focos hasta el pie de la torre es de 200 m. Si los ángulos que forman los haces de luz con el suelo son de 35º y 48º respectivamente. ¿Qué altura tiene el campanario?
13) Dos cámaras situadas en el suelo y en lados distintos, graban el vuelo de un avión. Las cámaras están a una distancia de 2.5 Km . Si los ángulos de elevación de dichas cámaras son de 75º y 35 º con el suelo, ¿a que altura se encuentra el avión?
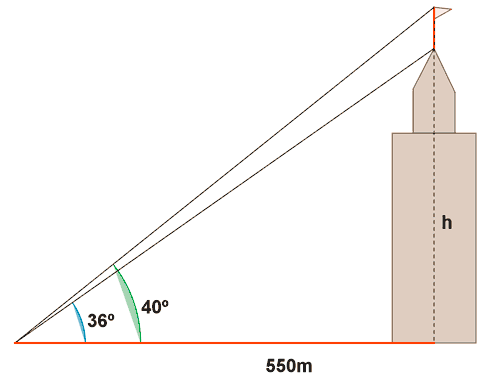
14) En lo alto de un edificio hay una antena. Desde una distancia de 550 m se ve la base de la antena con un ángulo de elevación de 36º y el extremo de dicha antena con un ángulo de elevación de 40º. Hallar la altura de la antena.
15) Dos individuos observan un globo que está situado en un plano vertical que pasa por eloos. La distancia entre los individuos se de 5 Km. Los ángulos de elevación del globo desde los observadores son 43º y 55º, respectivamente. Hallar la altura del globo, y su distancia a cada observador.
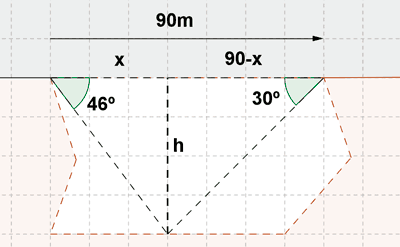
16) Para costruir un puente hemos tomado las medidas que se muestran en el dibujo.
a) ¿Qué longitud tendrá el puente?
b) ¿Cuál es la altura máxima de los pilares que lo sujetan?
17) Calcular la altura a la que circulan los vehiculos por un puente que atraviesa un desfiladero con las medidas representadas en el dibujo.
Ejercicios resueltos de triángulos rectángulos I
Ejercicios resueltos de triángulos rectángulos III
1) Un globo está sujeto al suelo mediante un cordel de 50 m de largo, que forma con el suelo un ángulo de 48º por efecto del viento. Suponiendo que nuestro cordel está completamente recto, calcular la altura del globo.
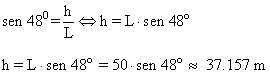
2) Se recorren 150 m en una carretera salvando un desnivel de 10 m. ¿Cual es el ángulo de inclinación de la carretera?

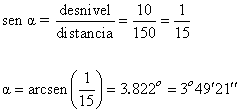
3) Desde un punto en el suelo situado a 50 m del pie de una antena, se traza la visual a la cúspide de la antena con un ángulo de 48º. ¿ cuál es la altura de la antena?
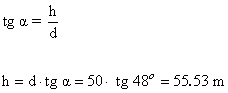
4) Juan y Pedro ven un árbol en la otra orilla del río que está frente a ellos. Al caminar Juan por la orilla una distancia de 150 metros mide el ángulo de elevación de esta orilla a la parte más alta del árbol y se obtiene un ángulo de 62º. ¿Cuál es el ancho del río?
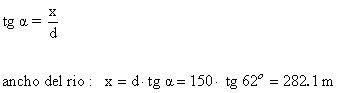
5) ¿Cuál es la inclinación de los rayos del sol si un mástil de una bandera de 3m de altura proyecta una sombra sobre el suelo de 1.2 m?
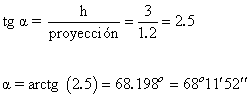
6) Un avión despega desde Barajas y lleva recorrido una distancia de 3 Km. Si el ángulo de elevación es de 15º. Calcular la altura del avión.
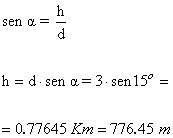
7) Un piloto que vuela a una altitud de 300 m señala que su ángulo de depresión a la torre de control es de 18 °. Si el avión sigue volando a esta altitud hacia la torre de control, ¿ cuantos metros tiene que recorrer para llegar a la torre ?
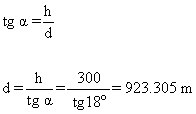
8) Desde un faro colocado a 35 m sobre el nivel del mar el ángulo de depresión de un barco es de 40º. ¿A que distancia del faro se halla el barco?
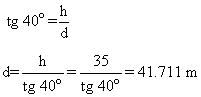
9) Si los dos brazos de un compás forman un ángulo de 60º y su longitud es de 10 cm. Hallar la distancia entre las puntas de los brazos.
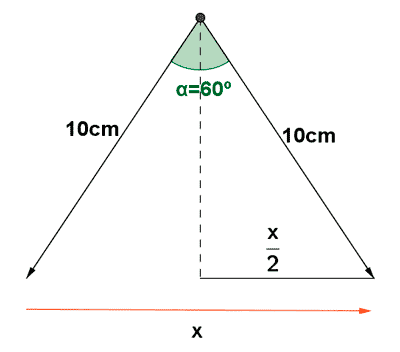
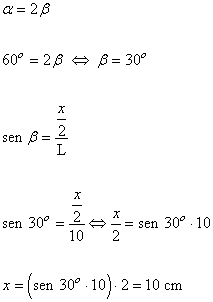
10) Se quiere medir la anchura de un río. Para ello se observa un árbol que está en la otra orilla a la parte más alta y se obtine un ángulo de elevación de 55º. Alejándose 5m del río en la misma dirección del árbol se vuelve a medir el ángulo de elecvación y se obtiene 42º. Calcula la anchura del río y la altura del árbol.
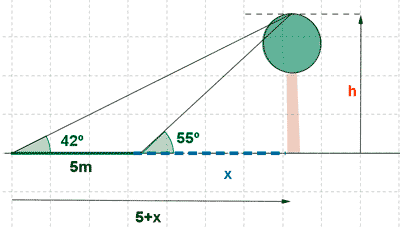

11) Dos amigos están en la base de una torre. Uno de ellos ve el extremo de la antena de la torre con un ángulo de 30º respecto a la horizontal y el otro con un ángulo de 45º. Si la distancia entre ambos es de 27 m, calcular la altura de la torre con su antena.
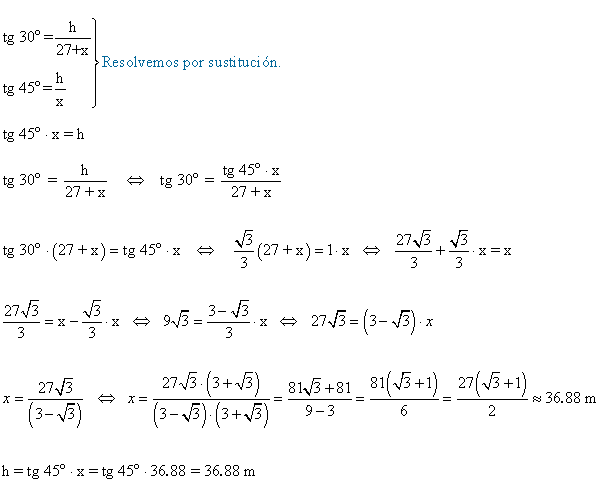
12) Dos focos situados en el suelo y en lados distintos, iluminan el campanario de una iglesia. La suma de las distancias de los focos hasta el pie de la torre es de 200 m. Si los ángulos que forman los haces de luz con el suelo son de 35º y 48º respectivamente. ¿Qué altura tiene el campanario?
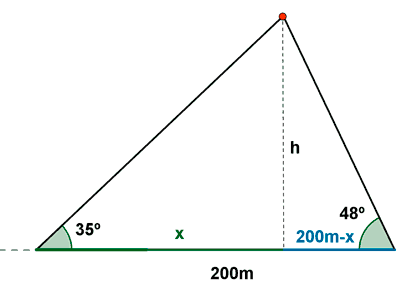
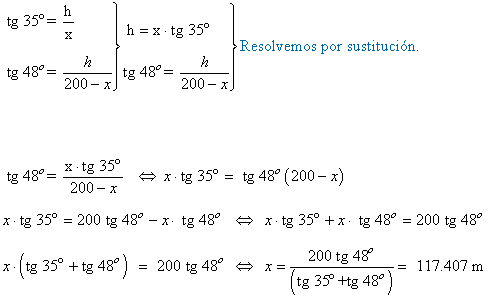
13) Dos cámaras situadas en el suelo y en lados distintos, graban el vuelo de un avión. Las cámaras están a una distancia de 2.5 Km . Si los ángulos de elevación de dichas cámaras son de 75º y 35 º con el suelo, ¿a qué altura se encuentra el avión?
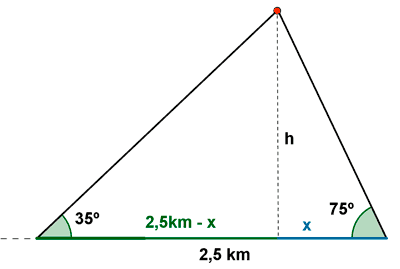
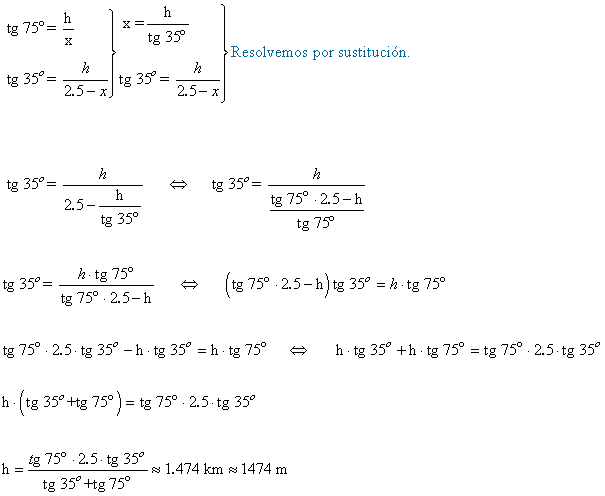
14) En lo alto de un edificio hay una antena. Desde una distancia de 550 m se ve la base de la antena con un ángulo de elevación de 36º y el extremo de dicha antena con un ángulo de elevación de 40º. Hallar la altura de la antena.
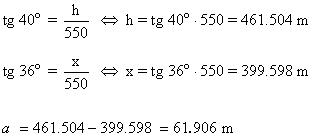
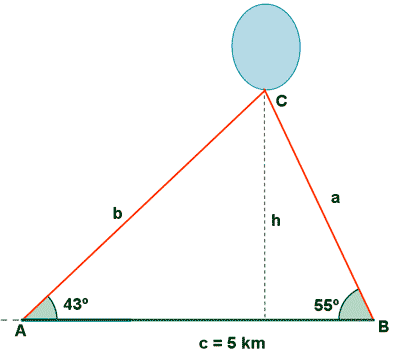
15) Dos individuos observan un globo que está situado en un plano vertical que pasa por eloos. La distancia entre los individuos se de 5 Km. Los ángulos de elevación del globo desde los observadores son 43º y 55º, respectivamente. Hallar la altura del globo, y su distancia a cada observador.
Hay que distinguir dos posiciones:
1- Los observadores están al mismo lado respecto de la vertical.
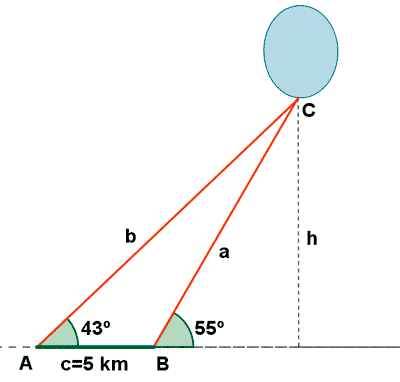
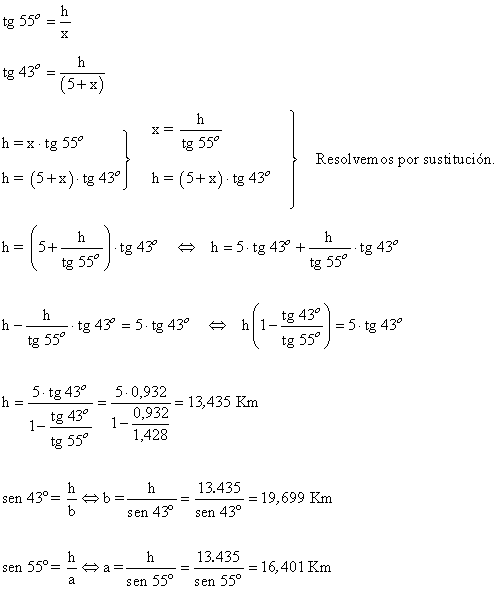
2- Los observadores están a distinto lado respecto de la vertical.
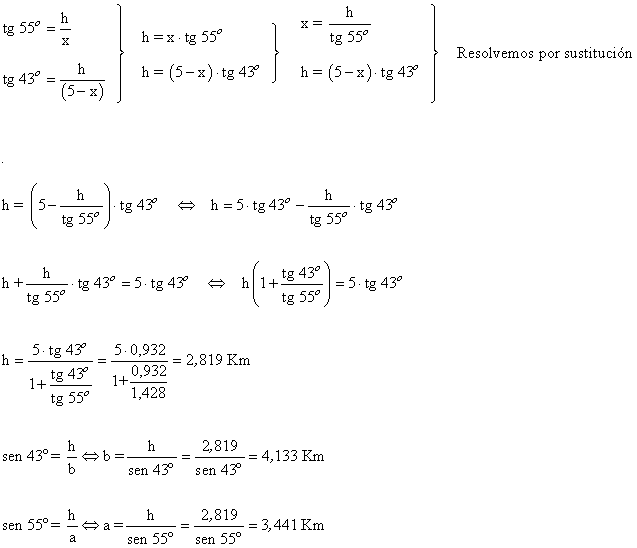
16) Para costruir un puente hemos tomado las medidas que se muestran en el dibujo.
a) ¿Qué longitud tendrá el puente?
b) ¿Cuál es la altura máxima de los pilares que lo sujetan?
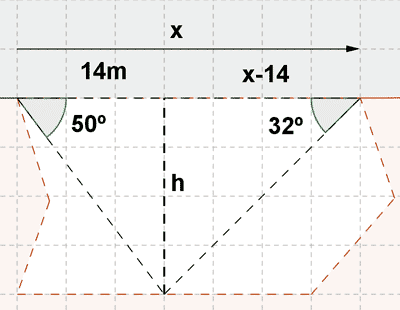

17) Calcular la altura de un puente que atraviesa un desfiladero con las medidas representadas en el dibujo.
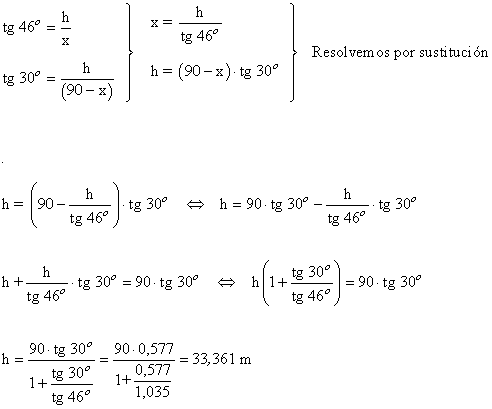


 INICIO
INICIO