INICIOVectores.
Un vector es un segmento orientado.
Dos puntos del plano, A y B, forman un vector fijo 
en el que A es el origen y B es el extremo.
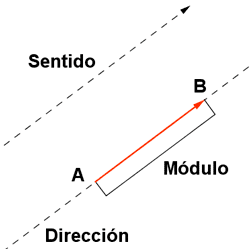
Un vector tiene las siguientes partes :
- Módulo : longitud del segmento AB o vector.
- Sentido : indica cuál de los dos puntos es el origen y cuál es el extremo.
- Dirección :recta que pasa por A y por B.
Coordenadas de un vector.
Dados los puntos del plano A ( x 1, y 1 ) y B ( x 2 , y 2 ) en un sistema de coordenadas cartesianas, las coordenadas del vector son = ( x 2 - x 1 , y 2 - y 1 ).
El módulo del vector se escribe | | y se define como :
Ejemplo 1 :
Halla las coordenadas y el módulo del vector :
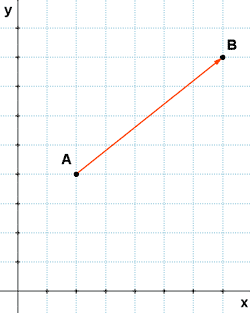
Las coordenadas de los puntos A y B son :
A ( 2, 4 ) y B ( 7, 8 ).
El vector que forman es :
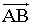= ( 7 - 2, 8 - 4 ) = ( 5, 4 ).
Su módulo es :
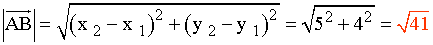
A ( 2, 4 ) y B ( 7, 8 ).
El vector que forman es :
= ( 7 - 2, 8 - 4 ) = ( 5, 4 ).Su módulo es :
Suma de vectores.
Podemos sumar vectores de dos formas
-
Suma de vectores de forma analítica : dados los vectores
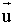= ( x 1 , y 1 ) y
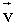= ( x 2 , y 2 ), llamaremos vector suma al vector 
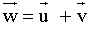cuyas componentes son :
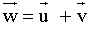= ( x 1 + x 2 , y 1 + y 2 ).
- Suma de vectores de forma geométrica : dibujamos el segundo vector de forma que su origen coincida con el extremo del primer vector. El vector suma se obtiene uniendo el origen del primer vector con el extremo del segundo vector.
Ejemplo 2 :
Suma, tanto analítica como geométricamente, los vectores ( 3, 4 ) y ( 5, 1 ).
Suma de forma geométrica.
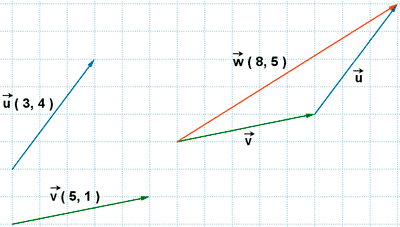
Suma de forma analítica.
= ( 3 + 5, 4 + 1 ) = ( 8, 5 )
