Problemas resueltos de recorrido de funciones 3º ESO
Estudia el dominio y el recorrido de las siguientes funciones:
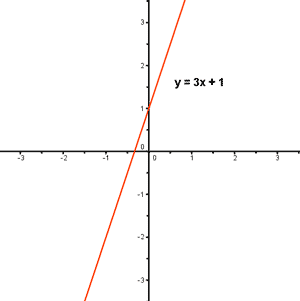
1) f(x) = 3x + 1
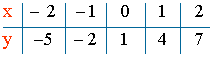
Dom (f) = R
Calculamos el recorrido:
Está bien definida para cualquier valor de y, por tanto:
Im (f) = R
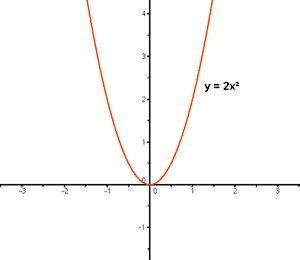
2) f(x) = 2x2
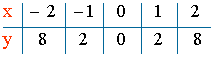
Dom (f) = R
Calculamos el recorrido:
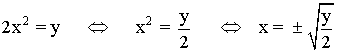
Para que esté bien definida:
![]()
Im (f) = [0 , ∞)
Estudia el dominio y el recorrido de las siguientes funciones:
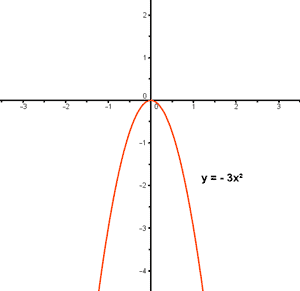
1) f(x) = -3x2
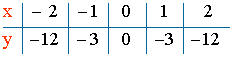
Dom (f) = R
Calculamos el recorrido:
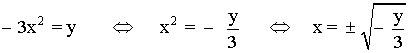
Para que esté bien definida:
![]()
Im (f) = (-∞ , 0]
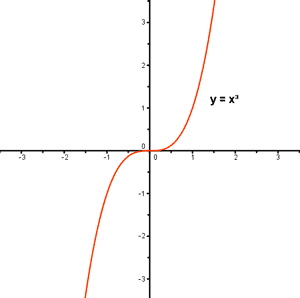
2) f(x) = x3
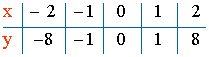
Dom (f) = R
Calculamos el recorrido:
![]()
Está bien definida para cualquier valor de y, por tanto:
Im (f) = R
Estudia el dominio y el recorrido de las siguientes funciones:
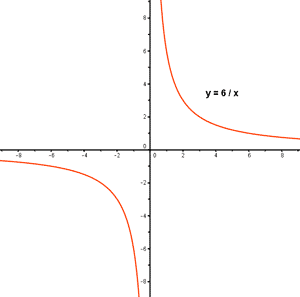
![]()
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
Luego si x = 0 , la función f no está definida.
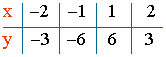
Dom (f) = R - {0}
Calculamos el recorrido:
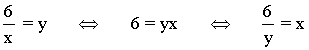
Para que esté bien definida no puede ser: y = 0
Además, no existe ningún valor de y para el que x tenga valor 0:
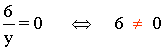
Im (f) = R - {0}
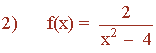
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
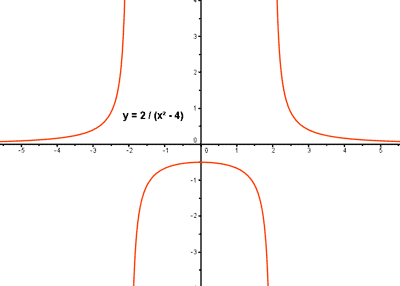
x2 - 4 = 0 ⇔ x2 = 4 ⇔ x = ±√4 ⇔ x = ±2
Dom (f) = R - {-2 , 2}
Calculamos el recorrido:
![]()
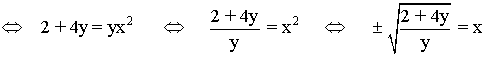
Para que esté bien definida el argumento de la raíz tiene que ser positivo:
y = 0 , 2 + 4y = 0 ⇔ y = 0 , y = - 1/2
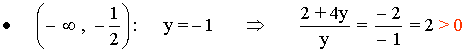
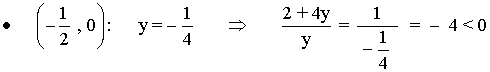
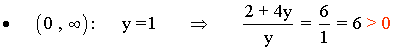
Nos quedamos con los intervalos: (-∞ , -1/2] ∪ (0 , ∞) = R - (-1/2 , 0]
Icluimos el valor x = -1/2 , ya que el argumento puede ser 0.
Además, no existe ningún valor de y para el que x tenga valor 2 ó - 2:
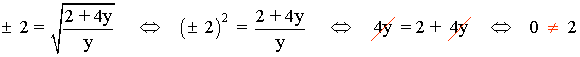
Im (f) = R - (-1/2 , 0]
Estudia el dominio y el recorrido de las siguientes funciones:
![]()
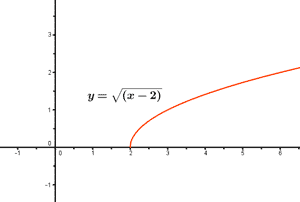
El dominio de f estará formado por aquellos
valores reales tales que: x - 2 ≥ 0
x - 2 ≥ 0 ⇔ x ≥ 2 ⇔ x ∈ [2 , ∞)
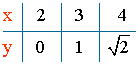
Dom (f) = [2 , ∞)
Calculamos el recorrido:
![]()
Está bien definida para todo valor de R, y además, observamos que: y2 + 2 ∈ R+ = [0 , ∞)
Im (f) = [0 , ∞)
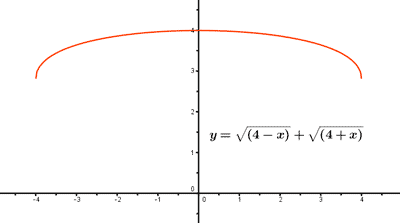
![]()
El dominio de f estará formado por aquellos
valores reales tales que: 4 - x ≥ 0 y 4 + x ≥ 0
4 - x ≥ 0 ⇔ 4 ≥ x ⇔ x ∈ (-∞ , 4]
4 + x ≥ 0 ⇔ x ≥ - 4 ⇔ x ∈ [-4, ∞)
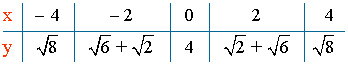
Dom (f) = (-∞ , 4] ∩ [-4, ∞) = [-4, 4]
Im (f) = [√8 , 4]


 INICIO
INICIO