Ejercicios del teorema del valor medio (teorema de Lagrange) y teorema de Cauchy
SELECTIVIDAD
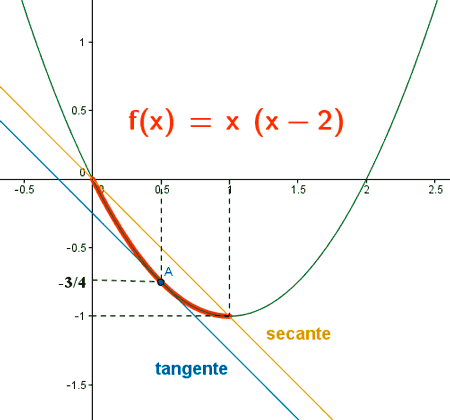
Indica si la función f(x) = x(x-2) verifica las hipótesis del teorema de valor medio (o teorema de Lagrange) en el intervalo [0, 1] y, en caso afirmativo, encontrar el punto intermedio cuya existencia asegura el teorema.
La función f(x) es una función polinómica, por lo que es continua y derivable en todo R y por tanto es continua en el intervalo [0, 1] y derivable en (0, 1) respectivamente.
Además, tenemos que: f(1) = -1 , f(0) = 0 y f ' (x) = 2x - 2
Por lo tanto, según el teorema del valor medio o teorema de Lagrange, tenemos que existe un punto c∈(-1, 0) tal que:
![]()
Luego el punto pedido es: A(1/2, -3/4)
SELECTIVIDAD
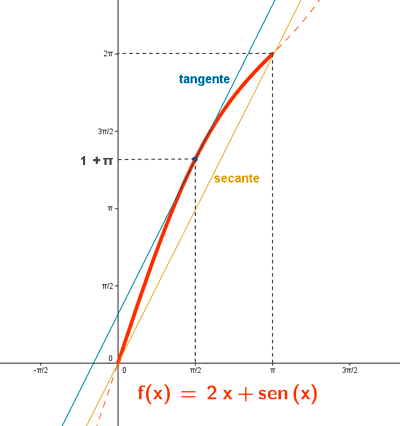
Indica si la función f(x) = 2x + sen x verifica las hipótesis del teorema de valor medio (o teorema de Lagrange) en el intervalo [0, π] y, en caso afirmativo, encontrar el punto intermedio cuya existencia asegura el teorema.
La función f(x) = 2x + sen x es continua en el intervalo [0, π] y derivable en (0, π) , por ser la suma de dos funciones continuas y derivables en R .
Además tenemos que: f(π) = 2π , f(0) = 0 y f ' (x) = 2 + cos x
Por lo tanto, según el teorema del valor medio o teorema de Lagrange, tenemos que existe un punto c∈(0, π) tal que:
![]()
Luego el punto pedido es: A(π/2, 1+π )
SELECTIVIDAD
Hallar un punto de la curva y = x2 donde la tangente es paralela a la cuerda de extremos los puntos (0, 0) y (2, 4).
Por tratarse de una función polinómica es continua y derivable en toda la recta real y en particular en el intervalo cerrado [0, 2] .
Por lo tanto se puede aplicar el teorema del valor medio, es decir, existe un punto c∈(0, 2) tal que:
![]()
![]()
Es decir, el punto es: A(1, 1).
SELECTIVIDAD
Sea f(x) = | cos x | en (-π, π)
¿Es aplicable el teorema del valor medio o teorema de Lagrange?
En caso afirmativo, hallar el valor que aparece en el teorema.
Como en la función interviene el valor absoluto, hay que definir la función por ramas:
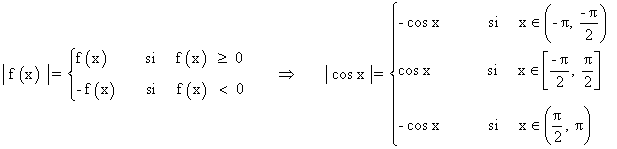
La función es continua en (-π, π) y derivable en (-π, -π/2) ∪ (-π/2, π/2) ∪ (π/2, π)
Por lo tanto, para ver que pasa en los puntos -π/2 y π/2 calculamos la derivada laterales aplicando la definición:
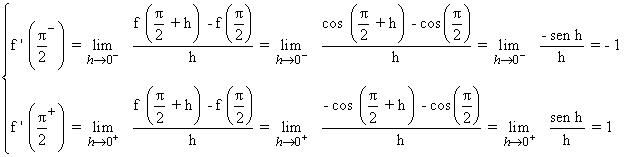
Por lo tanto no existe la derivada en π/2 .
De manera análoga, tampoco existe la derivada en -π/2 .
SELECTIVIDAD
Determinar, si es posible, a y b para que el teorema del valor medio (o teorema de Lagrange) sea aplicable a la siguiente función en el intervalo [-2, 0] :
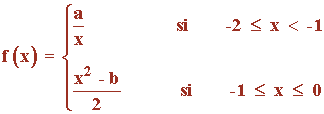
Para poder aplicar el teorema del valor medio o teorema de Lagrange, la función ha de ser continua en el intervalo [-2, 0] . Cada una de las ramas son funciones continuas en sus intervalos de definición, por lo que tenemos que estudiar la continuidad para el punto x = -1 :
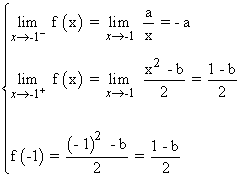
Por lo tanto, para que la función sea continua en x = -1 tiene que darse que:
![]()
Por otra parte, para aplicar el teorema del valor medio o teorema de Lagrange, la función tiene que ser derivable en el intervalo (-2, 0) :
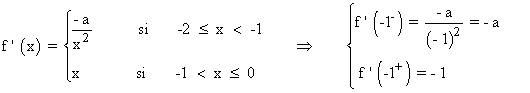
Es decir, para que la función sea derivable en el intervalo (-2, 0) tiene que cumplirse que: a = 1
Sustituyendo dicho valor en la condición que se obtuvo anteriormente, tenemos que:
![]()
Por lo tanto, para que se pueda aplicar el teorema del valor medio o teorema de Lagrange a la función, se tiene que cumplir que: a = 1 y b = 3
SELECTIVIDAD
¿ Se puede aplicar el teorema de Cauchy a las funciones f(x) = x2 + 2x + 1 y g(x) = x3 - 2x - 1 en el intervalo [-2, 1] ? En caso afirmativo, aplicarlo determinando el punto en que se verifica.
Ambas funciones, por ser polinómicas, son continuas en el intervalo [-2, 1] y derivables en (-2, 1) además de cumplirse que: g(-2) = -5 y g(1) = -2 ⇒ g(-2)≠g(1)
Por otra parte, tenemos que: g ' (x) = 3x2 - 2 ⇒ g ' (x) = 0 ⇔ 3x2 - 2 = 0
![]()
Es decir, se cumplen todas las condiciones del teorema de Cauchy. Por lo tanto, existe un punto c∈(-2, 1) tal que:
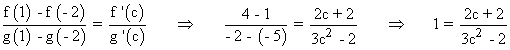
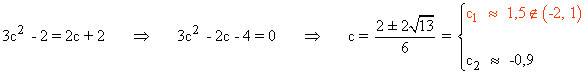
Por lo tanto el punto en el que se verifica el teorema es:
![]()
SELECTIVIDAD
Aplicar el teorema de Cauchy a las funciones f(x) = sen x y g(x) = cos x en el intervalo [0, π/2] .
Las funciones trigonométricas f(x) = sen x y g(x) = cos x son funciones continuas y derivables en todo R y por tanto lo son en el intervalo [0, π/2] y (0, π/2).
Además se cumple que:
• g(0) = 1 y g(π/2) = 0 ⇒ g(0)≠g(π/2)
• g ' (x) = - sen x ≠ 0 para todo x∈(0, π/2)
Es decir, se cumplen todas las condiciones del teorema de Cauchy.
Por lo tanto, existe un punto c∈(π/2) tal que:
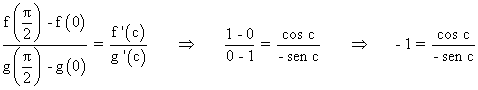
![]()
SELECTIVIDAD
¿ Se puede aplicar el teorema de Cauchy a las funciones f(x) = x2 y g(x) = x3 en el intervalo [-1, 1] ?
Las funciones polinómicas f(x) = x2 y g(x) = x3 son funciones continuas y derivables en todo R y por tanto lo son en el intervalo [-1, 1] y (-1, 1) respectivamente.
Además se cumple que: g(-1) = -1 y g(1) = 1 ⇒ g(-1)≠g(1)
Como g ' (x) = 3x2 = 0 cuando x = 0∈(-1, 1) no se puede aplicar el teorema de Cauchy a dichas funciones en el intervalo [-1, 1] .
SELECTIVIDAD
Sean f(x) = 3x4 - 2x3 - x2 + 1 y g(x) = 4x3 - 3x2 - 2x
Comprobar que no existe ningún punto t∈(0, 1) en el que se cumple:
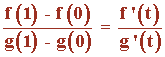
Las funciones polinómicas son funciones continuas y derivables en todo R y por tanto lo son en el intervalo [0, 1] y (0, 1) respectivamente.
Además se cumple que: g(0) = 0 y g(1) = -1 ⇒ g(0)≠g(1)
Por otra parte tenemos que:
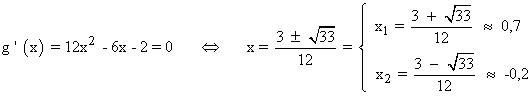
Es decir, existe un punto c∈(0, 1) tal que g ' (c) = 0 por lo que no se cumple una de las hipótesis del teorema de Cauchy.
Por lo tanto, no existe ningún punto t∈(0, 1) tal que:
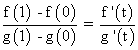


 INICIO
INICIO