Teorema de los valores intermedios (Darboux)
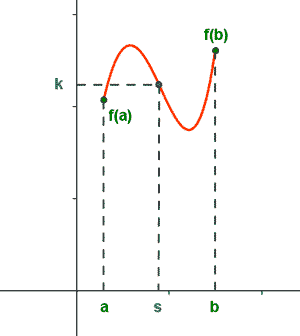
Si una función es continua en un intervalo cerrado [a, b] , entonces toma todos los valores intermedios entre f(a) y f(b) .
Es decir, para cualquier valor k comprendido entre f(a) y f(b) , existe un número s ∈ [a, b] , tal que f(s) = k .
El teorema de los valores intermedios es una consecuencia inmediata del teorema de Bolzano. Otra consecuencia es la siguiente:
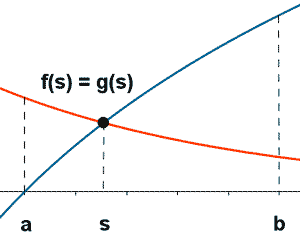
Si f(x) y g(x) son funciones continuas en [a, b] y f(a) < g(a) y f(b) > g(b) , entonces existe un número s ∈[a, b] tal que f(s) = g(s) .
Aplicación del Teorema de los valores intermedios
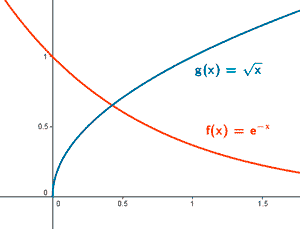
Probar que las gráficas de las funciones f(x) = e -x y g(x) = √x se cortan en algún punto.
Las funciones f(x) y g(x) son continuas en todo su dominio y en concreto en el intervalo [0, 1] . Además tenemos que:
f(0) = e0 = 1
f(1) = e -1 = 1/e ≈ 0,37
g(0) = √0 = 0
g(1) = √1 = 1
→ f(0) > g(0)
→ f(1) < g(1)
Por tanto, existe un punto s ∈ (0, 1) tal que f(s) = g(s) .


 INICIO
INICIO

