Ejercicios de teoremas de continuidad
Probar que la ecuación x3 - 4x - 2 = 0 tiene alguna raíz real, aproximando su valor hasta las décimas.
Consideramos la función f(x) = x3 - 4x - 2 la cual es continua por ser polinómica.
Tanteando, tenemos que f(2) = - 2 y f(3) = 13
Es decir, tenemos una función continua en el intervalo [2, 3] donde signo de f(2) ≠ signo de f(3) .
Por lo tanto, por el Teorema de Bolzano, existe un c ∈ [2, 3] tal que f(c) = 0 .
Para aproximar la solución a la décima seguimos tanteando: f(2,2) = - 0,152 y f(2,3) = 0,967
Tememos una función cotinua en el intervalo [2,2, 2,3] donde signo de f(2,2) ≠ signo de f(2,3) .
Es decir, existe un c ∈ [2,2, 2,3] tal que f(c) = 0 .
SELECTIVIDAD
Determinar si el polinomio x4 - 4x2 - 1 tiene alguna raíz real negativa.
Consideremos la función: f(x) = x4 - 4x2 - 1
Vamos a intentar aplicar el teorema de Bolzano para encontrar una raíz negativa del polinomio, es decir, para encontrar un valor de c < 0 que cumpla que f(c) = 0 .
La función f es continua en todo R por ser polinómica.
Tanteando con valores negativos, tenemos que:
f(-4) = 191 > 0
f(-1) = - 4 < 0
Por lo tanto, por el Teorema de Bolzano, existe un c ∈ [-4, -1] tal que f(c) = 0 .
La función se anula en algún punto del intervalo (-4 , -1) , por lo que el polinomio tiene una raíz negativa en dicho intervalo.
SELECTIVIDAD
Sea la función
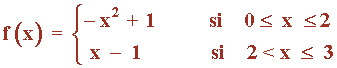
¿es continua?
Prueba que existe c ∈ [0 , 3] tal que f(c) = 0 . ¿Contradice el teorema de Bolzano?
Las funciones que definen la función f son polinómicas, luego son continuas para cualquier valor de la recta real, y en particular en lo son en el intervalo [0 , 3] .
El único valor en el que puede haber problema es en el de abscisa x = 2 . Estudiemos la continuidad de f en dicho punto:
f(2) = - 22 + 1 = - 3
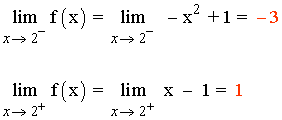
Como los límites laterales no coinciden la función f no es continua en x = 2 .
Puesto que la función f no es continua en todo el intervalo [0 , 3] , no podemos aplicar el teorema de Bolzano.
Sin embargo, podemos encontrar un c ∈ [0 , 3] tal que f(c) = 0 . Por ejemplo:
Si c = 1 ∈ [0 , 3] ⇒ f(1) = - 12 + 1 = 0
Esto no contradice el teorema. El que no se cumplan las condiciones del teorema de Bolzano no significa que no exista un valor de c en el que la función se anule.
SELECTIVIDAD
¿Puede asegurarse, utilizando el teorema de Bolzano, que la función f(x) = tg x tiene una raíz en el intervalo [π/4 , 3π/4] ?
Razona la respuesta
Sabemos que la función tangente no está definida en x = π/2 , y π/2 ∈ [π/4 , 3π/4].
Por tanto, la función f no es continua en todos los puntos del intervalo [π/4 , 3π/4] .
Como no cumple una de las condiciones del teorema de Bolzano, no podemos aplicarlo y asegurar que existe c∈[π/4 , 3π/4] tal que f(c) = 0.
Es decir, no podemos asegurar que f tenga una raíz en [π/4 , 3π/4].
SELECTIVIDAD
La función f se define en [-1 , 1] del siguiente modo: vale -1 si x ≤ 0 y vale 2x3 - 1 si x > 0 .
Explica si f verifica el teorema de Bolzano.
La función que nos describen es:
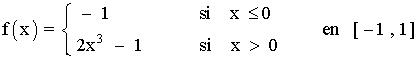
Las funciones que definen la función f son polinómicas, luego son continuas para cualquier valor de la recta real , en particular en el intervalo [-1 , 1] .
El único valor en el que puede haber problema es en el de abscisa x = 0 . Estudiemos la continuidad de f en dicho punto:
f(0) = - 1
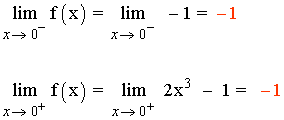
Como los límites laterales coinciden tenemos que:
![]()
Se cumple la condición de continuidad en x = 0 :
![]()
Por tanto, la función es continua en x = 0 , por lo que es continua en todo el intervalo [-1 , 1] .
Comprobamos que en los puntos x = -1 y x = 1 el signo de la función es distinto:
f(-1) = -1 < 0
f(1) = 2·12 - 1 = 1 > 0
Por tanto, la función f verifica el teorema de Bolzano en [-1 , 1] .
SELECTIVIDAD
Probar que la ecuación x = cos x tiene solución positiva.
Consideremos la función: f(x) = x - cos x
f(x) es continua en todo R puesto que es la suma de dos funciones continuas en todo R , por lo que es continua en el intervalo [0, 1] .
Además, tenemos que:
• f(0) = 0 - cos 0 = 0 - 1 = - 1 < 0
• f(1) = 1 - cos 1 = 1 - 0,54 = 0,46 > 0
Según el teorema de Bolzano, existe un c ∈ (0, 1) tal que f(c) = 0
Por lo tanto se demuestra que la ecuación tiene al menos una solución positiva.
SELECTIVIDAD
Enuncia el teorema de Bolzano. Aplícalo para demostrar que la ecuación 2x - 1 = 1 + (1 + x)2 tiene al menos una solución, determinando un intervalo (a , b) con a ∈ R , b ∈ R y a < b , en el cual se encuentre dicha solución.
Teorema de Bolzano: Si una función es continua en un intervalo cerrado [a, b] y signo f(a) ≠ signo f(b) , entonces existe un c ∈ [a, b] tal que f(c) = 0 .
Vamos a escribir la ecuación en forma de una función dependiente de la variable x :
2x - 1 = 1 + (1 + x)2 ⇔ 1 + (1 + x)2 - 2x - 1 = 0
Consideremos pues la función: f(x) = 1 + (1 + x)2 - 2x - 1
La función f es continua en todo R por ser suma de funciones continuas:
x → 1 + (1 + x)2 continua por ser polinómica
x → 2x - 1 continua por ser exponencial
Observamos que es dificil encontrar dos números a,b ∈ R tales que signo f(a)≠signo f(b) , así que vamos a calcular los límites en los extremos de la función, es decir, en ±∞ :
Calculando los límites por separado tenemos que:
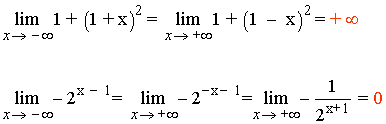
Luego:
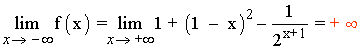
Por otro lado:
![]()
Y por comparación de infinitos (un infinito exponencial es mayor que el infinito de un polinomio) se tiene que:
![]()
Como el límite de f en -∞ tiene distinto signo que el límite de f en +∞ , podemos aplicar el teorema de Bolzano.
Por tanto, existe al menos un número real c ∈ R tal que f(c) = 0 , es decir, es solución de la ecuación del enunciado.
Vamos a intentar encontrar un intervalo que contenga a dicho c ∈ R .
f(7) = 1 + 82 - 26 = 1 > 0
f(8) = 1 + 81 - 27 = -46 < 0
Luego c ∈ (7 , 8) .
SELECTIVIDAD
Dadas las funciones f(x) = x·sen x y g(x) = ln x justifica que existe un punto del intervalo [2, 3] donde ambas funciones toman el mismo valor.
Consideremos la función: h(x) = x·sen x - ln x
f(x) es continua en todo R y g(x) lo es en (0, +∞) , por lo que h(x) es continua en el intervalo [2, 3] .
Además, tenemos que:
• h(2) = 1,12 > 0
• h(3) = -0,67 < 0
Según el teorema de Bolzano, existe un c ∈ (2, 3) tal que h(c) = 0
Es decir, h(c) = f(c) - g(c) = 0 ⇒ f(c) = g(c)
Por lo tanto las funciones f(x) y g(x) se cortan en algún punto de dicho intervalo.
SELECTIVIDAD
Demostrar que las funciones f(x) = ex y g(x) = 1/x se cortan en algún punto x > 0 :
Consideremos la función: h(x) = ex - 1/x
f(x) es continua en todo R y g(x) en R - {0} , por lo que h(x) es continua en R - {0} .
Además, tenemos que:
• h(0,5) = -0,35 < 0
• h(1) = 1,72 > 0
Según el teorema de Bolzano, existe un c ∈ (0,5, 1) tal que h(c) = 0
Es decir, h(c) = f(c) - g(c) = 0 ⇒ f(c) = g(c)
Por lo tanto las funciones f(x) y g(x) se cortan en algún punto de dicho intervalo.
SELECTIVIDAD
Demostrar que las funciones f(x) = ln x y g(x) = e-x se cortan en algún punto y localizarlo aproximadamente:
Consideremos la función: h(x) = ln x - e-x
f(x) es continua en (0, +∞) y g(x) en R , por lo que h(x) es continua en (0, +∞) .
Además, tenemos que:
• h(1) = ln 1 - e-1 = 0 - 1/e < 0 0
• h(e) = ln e - e-e = 1 - 1/ee > 01,72 > 0
Según el teorema de Bolzano, existe un c ∈ (1, e) tal que h(c) = 0
Es decir, h(c) = f(c) - g(c) = 0 ⇒ f(c) = g(c)
Por lo tanto las funciones f(x) y g(x) se cortan en algún punto de dicho intervalo.
SELECTIVIDAD
Demostrar que la siguiente función alcanza máximo y mínimo absolutos en el intervalo [-1, 1] y calcularlos.
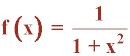
El denominador de la función no se anula para ningún valor de x puesto que 1 + x2 ≥ 1 .
Por lo tanto, la función es continua en el intervalo [-1, 1] .
Aplicando el teorema de Wierstrass (o teorema del máximo-mínimo), la función alcanza máximo y mínimo absolutos en ese intervalo.
Para calcular los máximos y los mínimos de la función estudiamos entre que valores oscila la función para el intervalo dado.
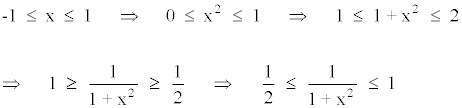
Es decir, el valor mínimo de la función es 1/2 y el valor máximo 1 .
Para calcular en que puntos se alcanzan el mínimo y el máximo, resolvemos las siguiente igualdades:
![]()
![]()
Por lo tanto la función alcanza un máximo absoluto en el punto (0, 1) y el mínimo absoluto lo alcanza en los puntos (-1, 1/2) y (1, 1/2) .


 INICIO
INICIO