Teorema de Weierstrass: Teorema del máximo y del mínimo

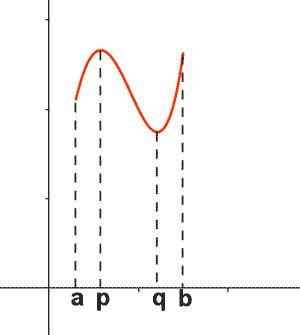
Si una función es continua en un intervalo cerrado   [a, b] ,  entonces tiene un mínimo (p) y un máximo (q) absolutos en ese intervalo. Es decir, existen dos números   p   y   q   del intervalo   [a, b]   para los cuales se cumple que:

Para cualquier valor   x ∈ [a, b]   se cumple que   f(p) ≤ f(x) ≤ f(q) .